MATLAB int()函数的用法(附带实例)
函数的积分是微分的逆运算,即由已知导数求原函数的过程。函数的积分有不定积分与定积分两种运算:
定积分中,若积分区间为无穷区间或被积函数在积分区间上有无穷不连续点,但积分存在或收敛,则称为广义积分。
在 MATLAB 中,利用 int() 函数不仅可以计算函数的不定积分,还可计算函数的定积分及广义积分,该函数的调用格式如下:
一般来说,当多次使用 int() 函数时,计算的就是多重积分;当积分下限 a 或积分上限 b 或上下限 a、b 均为无穷大时,计算的就是广义积分,广义积分是相对于常义积分而言的。
【实例】已知导函数:
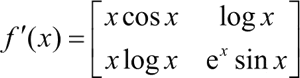
试求原函数 f(x)。
在命令行窗口中输入以下语句,并查看输出结果:
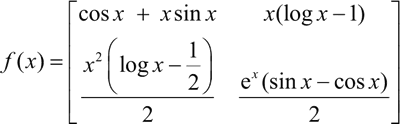
- 不定积分:求一个给定函数作为导函数的原函数的运算,称为不定积分,这确实是积分学的第一个基本问题。也就是说,寻找一个函数,使其导数等于给定函数。
- 定积分:被积函数在积分的上下限区间的计算问题,即求一个函数在某一区间上的累积量,这是定积分,属于积分学的第二个基本问题。牛顿-莱布尼茨公式给出了定积分与原函数的关系,是解决定积分问题的重要工具。该公式表明,定积分可以通过计算不定积分在积分上下限处的函数值之差来得到。
定积分中,若积分区间为无穷区间或被积函数在积分区间上有无穷不连续点,但积分存在或收敛,则称为广义积分。
在 MATLAB 中,利用 int() 函数不仅可以计算函数的不定积分,还可计算函数的定积分及广义积分,该函数的调用格式如下:
F=int(expr) % 计算符号表达式 expr 的不定积分
% 使用由 symvar(expr,1) 确定的默认积分变量,若 expr 是常数,则默认积分变量为 x
F=int(expr,var) % 计算符号表达式 expr 关于符号变量 var 的不定积分
F=int(expr,a,b) % 计算符号表达式 expr 从 a 到 b 的定积分,与 int(expr,[a b])等效
F=int(expr,var,a,b) % 计算符号表达式 expr 关于符号变量 var 从 a 到 b 的定积分
% 与 int(expr,var,[a b])等效
F=int(___,Name,Value) % 使用一个或多个 Name-Value 对来指定其他选项
注意,函数 int() 可计算函数的不定积分,不包含积分常数这一部分;高等数学中,有分部积分、换元积分、分解成部分分式的积分等各种积分方法,但在 MATLAB 中,都只使用 int() 函数来计算。一般来说,当多次使用 int() 函数时,计算的就是多重积分;当积分下限 a 或积分上限 b 或上下限 a、b 均为无穷大时,计算的就是广义积分,广义积分是相对于常义积分而言的。
【实例】已知导函数:
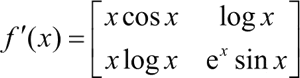
试求原函数 f(x)。
在命令行窗口中输入以下语句,并查看输出结果:
>> syms x;
>> dfdx=[x*cos(x) log(x); x*log(x) exp(x)*sin(x)]
dfdx =
[x*cos(x), log(x)]
[x*log(x), exp(x)*sin(x)]
>> fx=int(dfdx)
fx =
[ cos(x)+x*sin(x), x*(log(x)-1)]
[(x^2*(log(x)-1)/2), -(exp(x)*(cos(x)-sin(x)))/2]
得证: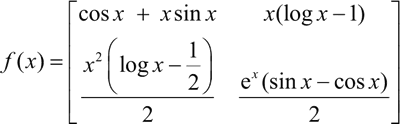
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: