MATLAB view()函数的用法(附带实例)
在现实空间中,从不同角度或位置观察某一物体往往会有不同的效果,即会有“横看成岭侧成峰”的感觉。三维图形表现的正是一个空间内的图形,因此在不同视角及位置都会有不同的效果,这在工程实际中也是经常遇到的。
MATLAB 提供的 view() 函数能够很好地满足这种需要。view() 函数用来控制三维图形的观察点和视角,它的调用格式及说明如下表所示。
对于这个函数需要说明的是,方位角 az 与仰角 el 为两个旋转角度。做一个通过视点和 z 轴平行的平面,与 xy 平面有一条交线,该交线与 y 轴的反方向的、按逆时针方向(从 z 轴的方向观察)计算的夹角就是观察点的方位角 az。若角度为负值,则按顺时针方向计算。在通过视点与 z 轴的平面上,用一条直线连接视点与坐标原点,该直线与 xy 平面的夹角就是观察点的仰角 el。若仰角为负值,则观察点转移到曲面下面。
【实例】在同一窗口中绘制半径变化的柱面的各种视图。MATLAB 程序如下:

图 1 视图转换
【实例 2】在区域 x∈[−π,π],y∈[−π,π] 上绘制下面函数不同视角的三维表面图。
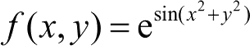
MATLAB 程序如下:
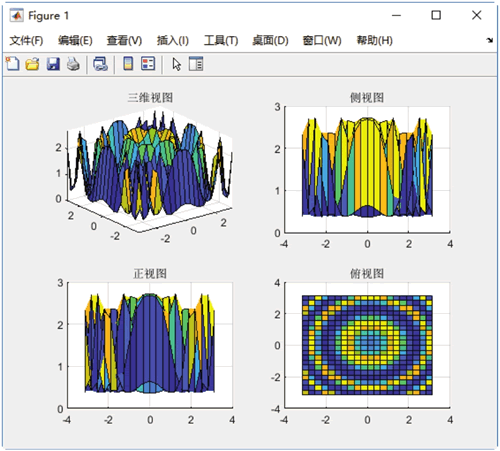
图 2 转换视角的三维表面图
MATLAB 提供的 view() 函数能够很好地满足这种需要。view() 函数用来控制三维图形的观察点和视角,它的调用格式及说明如下表所示。
| 调用格式 | 说明 |
|---|---|
| view(az,el) | 给三维图形设置观察点的方位角 az 与仰角 el |
| view([az,el]) | 同上 |
| view([x,y,z]) | 将点(x,y,z)设置为视点 |
| view(2) | 设置默认的二维形式视点,其中 az=0,el=90°,即从 z 轴上方观看 |
| view(3) | 设置默认的三维形式视点,其中 az=-37.5°,el=30° |
| [az,el] = view | 返回当前的方位角 az 与仰角 el |
| view(ax,...) | 指定目标坐标区的角度 |
对于这个函数需要说明的是,方位角 az 与仰角 el 为两个旋转角度。做一个通过视点和 z 轴平行的平面,与 xy 平面有一条交线,该交线与 y 轴的反方向的、按逆时针方向(从 z 轴的方向观察)计算的夹角就是观察点的方位角 az。若角度为负值,则按顺时针方向计算。在通过视点与 z 轴的平面上,用一条直线连接视点与坐标原点,该直线与 xy 平面的夹角就是观察点的仰角 el。若仰角为负值,则观察点转移到曲面下面。
【实例】在同一窗口中绘制半径变化的柱面的各种视图。MATLAB 程序如下:
>> close all % 关闭当前已打开的文件
>> clear % 清除工作区的变量
>> t=0:pi/10:2*pi; % 创建0~2π的向量x,元素间隔为π/10
%{返回圆柱体的x轴、y轴、z轴的坐标值X、Y、Z,圆柱体半径为以t为自变量的函数表达式,创建的圆柱体
半径可变、高度为1,圆柱体的圆周有30个距离相同的点%}
>> [X,Y,Z]=cylinder(sin(2*t),30);
>> subplot(2,2,1) % 将视图分割为2×2的4个窗口,在第1个窗口中绘图
>> surf(X,Y,Z),title('三维视图') % 为图形添加标题
>> subplot(2,2,2) % 将视图分割为2×2的4个窗口,在第2个窗口中绘图
% 根据x轴、y轴、z轴的坐标值X、Y、Z绘制曲面图,使用 90 度的方位角和 0 度的仰角查看绘图
>> surf(X,Y,Z),view(90,0)
>> title('侧视图') % 为图形添加标题
>> subplot(2,2,3) % 将视图分割为2×2的4个窗口,在第3个窗口中绘图
% 根据x轴、y轴、z轴的坐标值X、Y、Z绘制曲面图,使用 0 度的方位角和 0 度的仰角查看绘图
>> surf(X,Y,Z),view(0,0)
>> title('正视图') % 为图形添加标题
>> subplot(2,2,4) % 将视图分割为2×2的4个窗口,在第4个窗口中绘图
% 根据x轴、y轴、z轴的坐标值X、Y、Z绘制曲面图,使用 0 度的方位角和 90 度的仰角查看绘图
>> surf(X,Y,Z),view(0,90)
>> title('俯视图') % 为图形添加标题
运行结果为:

图 1 视图转换
【实例 2】在区域 x∈[−π,π],y∈[−π,π] 上绘制下面函数不同视角的三维表面图。
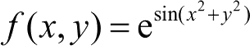
MATLAB 程序如下:
>> close all % 关闭当前已打开的文件
>> clear % 清除工作区的变量
>> [X,Y]=meshgrid(-pi:0.1*pi:pi); % 创建-π到π的向量x,元素间隔为π/10。
>> Z=exp(sin(X.^2+Y.^2)); % 通过网格数据X、Y定义函数表达式 Z,得到二维矩阵Z
>> subplot(2,2,1) % 将视图分割为2×2的4个窗口,在第1个窗口中绘图
>> surf(X,Y,Z),title('三维视图') % 为图形添加标题
>> subplot(2,2,2) % 将视图分割为2×2的4个窗口,在第2个窗口中绘图
% 根据x轴、y轴、z轴的坐标值X、Y、Z绘制曲面图,使用 90 度的方位角和 0 度的仰角查看绘图
>> surf(X,Y,Z),view(90,0)
>> title('侧视图') % 为图形添加标题
>> subplot(2,2,3) % 将视图分割为2×2的4个窗口,在第3个窗口中绘图
% 根据x轴、y轴、z轴的坐标值X、Y、Z绘制曲面图,使用 0 度的方位角和 0 度的仰角查看绘图
>> surf(X,Y,Z),view(0,0)
>> title('正视图') % 为图形添加标题
>> subplot(2,2,4) % 将视图分割为2×2的4个窗口,在第4个窗口中绘图
% 根据x轴、y轴、z轴的坐标值X、Y、Z绘制曲面图,使用 0 度的方位角和 90 度的仰角查看绘图
>> surf(X,Y,Z),view(0,90)
>> title('俯视图') % 为图形添加标题
运行结果为:

图 2 转换视角的三维表面图
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: