MATLAB linprog()函数解线性规划问题(非常详细)
通常,线性规划问题的标准形式表述为:
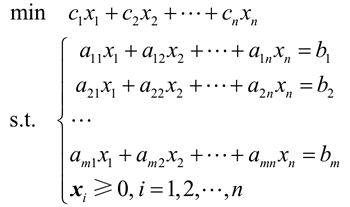
线性规划问题的标准型要求如下:
上式用矩阵形式简写为:
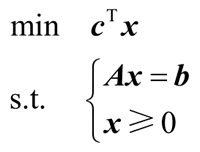
为了使约束集不为空集以及避免冗余约束,通常假设 A 行满秩且 m≤n。
但在实际问题中,建立的线性规划数学模型并不一定都有上边第 2 个式子的形式,如有的模型还有不等式约束、对自变量 x 的上下界约束等。这时,可以通过简单的变换将它们转化成标准形式。
非标准型线性规划问题过渡到标准型线性规划问题的处理方法有如下几种:
关于具体的变换方法,在这里就不再详述,感兴趣的读者可以查阅相关资料。
在线性规划中,普遍存在配对现象,即对一个线性规划问题,存在一个与之有密切关系的线性规划问题,其中之一为原问题,而另一个称为它的对偶问题。例如,对于线性规划标准形,其对偶问题为下面的最大化问题:
对于线性规划问题,如果原问题有最优解,那么其对偶问题也一定存在最优解,且它们的最优值是相等的。解线性规划问题的许多算法都可以同时求出原问题和对偶问题的最优解。
在 MATLAB 中,解线性规划的函数是 linprog(),它的调用格式如下:
1) x=linprog(c,A,b)。求解如下形式的线性规划:
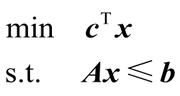
2) x=linprog(c,A,b,Aeq,beq)。求解如下形式的线性规划:
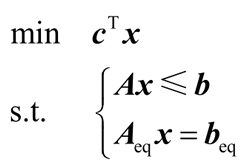
若没有不等式约束 Ax≤b,则只需令 A=[ ],b=[ ]。
3) x=linprog(c,A,b,Aeq,beq,lb,ub)。求解如下形式的线性规划:
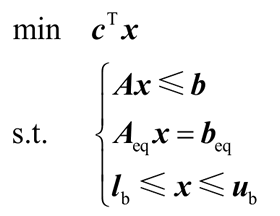
若没有不等式约束 Ax≤b,则只需令 A=[ ],b=[ ];若只有下界约束,则可以不用输入 ub。
4) x=linprog(problem)。求解结构体 problem 指定的最小化问题。
5) x=linprog(c,A,b,Aeq,beq,lb,ub,x0,options)。解形式 3) 的线性规划,将初值设置为 x0,options 为指定的优化参数(具体见下表),利用 optimset() 函数设置这些参数。
6) [x,fval]=linprog(…)。除了返回线性规划的最优解 x 外,还返回目标函数最优值 fval,即 fval=cTx。
7) [x, fval, exitflag,output]=linprog(…)。除了返回线性规划的最优解 x 及最优值 fval 外,还返回终止迭代的条件信息 exitflag 和关于优化算法的信息变量 output,exitflag 的值及相应的说明见下表:
output 的结构及相应的说明见下表:
8) [x, fval, exitflag, output, lambda]=linprog(…)。在上个函数的基础上,输出各种约束对应的拉格朗日乘子(即相应的对偶变量值),它是一个结构体变量,其内容如下表所示。
【实例 1】对于下面的线性规划问题:
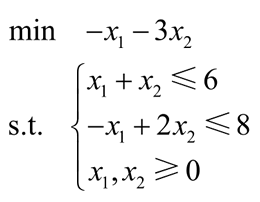
利用图解法求其最优解。
利用 MATLAB 画出该线性规划的可行解及目标函数等值线。在 MATLAB 命令行窗口输入以下命令:
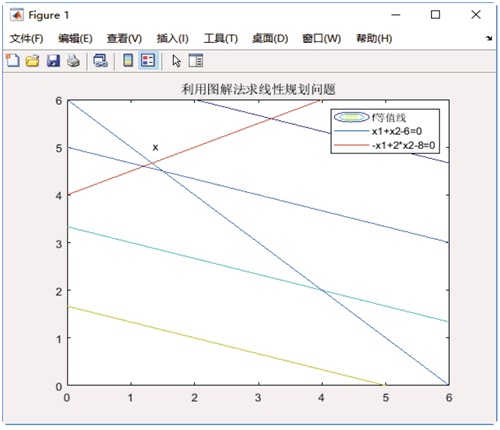
图 7 图解法解线性规划
从图 7 中可以看出,可行解的顶点 x(4/3, 14/3) 即线性规划的最优解,它也是两个线性约束的交点。
【实例 2】对于上面的线性规划问题利用优化工具箱中的 linprog() 函数求解。在 MATLAB 命令行窗口输入以下命令:
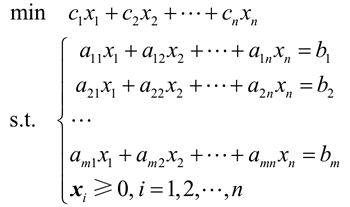
线性规划问题的标准型要求如下:
- 所有的约束必须是等式约束;
- 所有的变量为非负变量;
- 目标函数的类型为最小化。
上式用矩阵形式简写为:
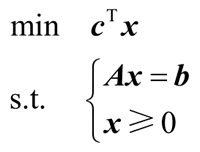
- A=(aij)m×n∈Rm×n 为约束矩阵;
- c=(c1,c2,…,cn)T∈Rn 为目标函数系数向量;
- b=(b1,b2,…,bm)T∈Rm;
- x=(x1,x2,…,xn)T∈Rn。
为了使约束集不为空集以及避免冗余约束,通常假设 A 行满秩且 m≤n。
但在实际问题中,建立的线性规划数学模型并不一定都有上边第 2 个式子的形式,如有的模型还有不等式约束、对自变量 x 的上下界约束等。这时,可以通过简单的变换将它们转化成标准形式。
非标准型线性规划问题过渡到标准型线性规划问题的处理方法有如下几种:
- 将最大化目标函数转化为最小化负的目标函数值;
- 把不等式约束转化为等式约束,可在约束条件中添加松弛变量;
- 若决策变量无非负要求,可用两个非负的新变量之差代替。
关于具体的变换方法,在这里就不再详述,感兴趣的读者可以查阅相关资料。
在线性规划中,普遍存在配对现象,即对一个线性规划问题,存在一个与之有密切关系的线性规划问题,其中之一为原问题,而另一个称为它的对偶问题。例如,对于线性规划标准形,其对偶问题为下面的最大化问题:
max λTb s.t. ATλ≤c其中,λ 称为对偶变量。
对于线性规划问题,如果原问题有最优解,那么其对偶问题也一定存在最优解,且它们的最优值是相等的。解线性规划问题的许多算法都可以同时求出原问题和对偶问题的最优解。
MATLAB linprog()函数的用法
在优化理论中,将线性规划化为标准形是为了理论分析的方便,但在实际中,这将会带来一点麻烦。幸运的是,MATLAB 提供的优化工具箱可以解决各种形式的线性规划问题,而不用转化为标准形式。在 MATLAB 中,解线性规划的函数是 linprog(),它的调用格式如下:
1) x=linprog(c,A,b)。求解如下形式的线性规划:
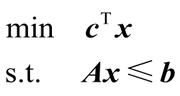
2) x=linprog(c,A,b,Aeq,beq)。求解如下形式的线性规划:
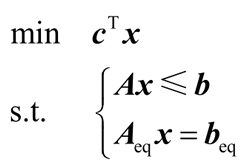
若没有不等式约束 Ax≤b,则只需令 A=[ ],b=[ ]。
3) x=linprog(c,A,b,Aeq,beq,lb,ub)。求解如下形式的线性规划:
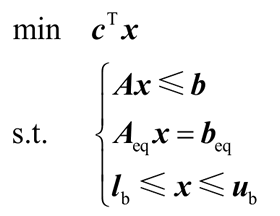
若没有不等式约束 Ax≤b,则只需令 A=[ ],b=[ ];若只有下界约束,则可以不用输入 ub。
4) x=linprog(problem)。求解结构体 problem 指定的最小化问题。
5) x=linprog(c,A,b,Aeq,beq,lb,ub,x0,options)。解形式 3) 的线性规划,将初值设置为 x0,options 为指定的优化参数(具体见下表),利用 optimset() 函数设置这些参数。
| 优化参数 | 说明 |
|---|---|
| LargeScale | 若设置为 on,则使用大规模算法;若设置为 off,则使用中小规模算法 |
| Diagnostics | 打印要最小化的函数的诊断信息 |
| Display | 设置为 off,不显示输出;设置为 iter,显示每一次的迭代输出;设置为 final,只显示最终结果 |
| MaxIter | 函数所允许的最大迭代次数 |
| Simplex | 如果设置为 on,则使用单纯形算法求解(仅适用于中小规模算法) |
| TolFun | 函数值的容忍度 |
6) [x,fval]=linprog(…)。除了返回线性规划的最优解 x 外,还返回目标函数最优值 fval,即 fval=cTx。
7) [x, fval, exitflag,output]=linprog(…)。除了返回线性规划的最优解 x 及最优值 fval 外,还返回终止迭代的条件信息 exitflag 和关于优化算法的信息变量 output,exitflag 的值及相应的说明见下表:
| exitflag 的值 | 说明 |
|---|---|
| 3 | 表示 x 对于相对容差 ConstraintTolerance 是可行解,对于绝对容差是不可行解 |
| 1 | 表示函数收敛到解 x |
| 0 | 表示达到了函数最大评价次数或迭代的最大次数 |
| -2 | 表示没有找到可行解 |
| -3 | 表示所求解的线性规划问题是无界的 |
| -4 | 表示在执行算法的时候遇到了 NaN |
| -5 | 表示原问题和对偶问题都是不可行的 |
| -7 | 表示搜索方向使得目标函数值下降得很少 |
| -9 | 表示无可行解 |
output 的结构及相应的说明见下表:
| output 结构 | 说明 |
|---|---|
| iterations | 表示算法的迭代次数 |
| algorithm | 表示求解线性规划问题时所用的优化算法 |
| cgiterations | 表示共轭梯度迭代(如果用的话)的次数 |
| constrviolation | 约束函数的最大值 |
| firstorderopt | 一阶最优性测量 |
| message | 表示算法退出的信息 |
8) [x, fval, exitflag, output, lambda]=linprog(…)。在上个函数的基础上,输出各种约束对应的拉格朗日乘子(即相应的对偶变量值),它是一个结构体变量,其内容如下表所示。
| lambda 结构 | 说明 |
|---|---|
| ineqlin | 表示不等式约束对应的拉格朗日乘子向量 |
| eqlin | 表示等式约束对应的拉格朗日乘子向量 |
| upper | 表示上界约束 x≤ub 对应的拉格朗日乘子向量 |
| lower | 表示下界约束 x≤lb 对应的拉格朗日乘子向量 |
【实例 1】对于下面的线性规划问题:
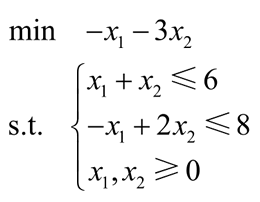
利用图解法求其最优解。
利用 MATLAB 画出该线性规划的可行解及目标函数等值线。在 MATLAB 命令行窗口输入以下命令:
>> close all % 关闭当前已打开的文件
>> clear % 清除工作区的变量
>> syms x1 x2 % 定义符号变量x1和x2
>> f=-x1-3*x2; % 定义符号表达式
>> c1=x1+x2-6;
>> c2=-x1+2*x2-8;
>> fcontour(f) % 绘制函数的等值线
>> axis([0 6 0 6]) % 设置坐标轴范围
>> hold on % 保留当前坐标区中的绘图
>> fimplicit(c1) % 绘制隐函数c1的图像
>> fimplicit(c2) % 绘制隐函数c2的图像
>> legend('f等值线','x1+x2-6=0','-x1+2*x2-8=0') % 添加图例
>> title('利用图解法求线性规划问题') % 添加标题
>> gtext('x') % 在图窗中添加文本
运行结果如下图所示:
图 7 图解法解线性规划
从图 7 中可以看出,可行解的顶点 x(4/3, 14/3) 即线性规划的最优解,它也是两个线性约束的交点。
【实例 2】对于上面的线性规划问题利用优化工具箱中的 linprog() 函数求解。在 MATLAB 命令行窗口输入以下命令:
>> close all % 关闭当前已打开的文件
>> clear % 清除工作区的变量
>> c=[-1 -3]; % 输入目标函数系数向量
>> A=[1 1;-1 2]; % 输入不等式约束系数矩阵
>> b=[6 8]; % 输入右端项
>> lb=zeros(2,1); % 创建 2x1 全零矩阵作为下限
>> [x,fval,exitflag,output,lambda]=linprog(c,A,b,[],[],lb) % 求解
Optimization terminated.
x = % 最优解
1.3333
4.6667
fval = % 最优值
-15.3333
exitflag = % 说明该算法对于该问题是收敛的
1
output =
包含以下字段的 struct:
iterations: 2 % 迭代次数
constrviolation: 0 % 达到了最优解,终止迭代
message: 'Optimal solution found.' % 达到了最优解,终止迭代
algorithm: 'dual-simplex' % 算法
firstorderopt: 6.6613e-16 % 一阶最优性测量
lambda = % 拉格朗日乘子向量
包含以下字段的 struct:
lower: [2x1 double] % 下界约束对应的拉格朗日乘子向量
upper: [2x1 double] % 上界约束对应的拉格朗日乘子向量
eqlin: [] % 等式约束对应的拉格朗日乘子,因为没有等式约束,所以为空
ineqlin: [2x1 double] % 不等式约束对应的拉格朗日乘子
>> lambda.ineqlin % 不等式约束对应的拉格朗日乘子
ans =
1.6667
0.6667
>> lambda.eqlin % 等式约束对应的拉格朗日乘子,因为没有等式约束,所以为空
ans =
[]
>> lambda.upper % 上界约束对应的拉格朗日乘子
ans =
0
0
>> lambda.lower % 下界约束对应的拉格朗日乘子
ans =
0
0
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: