MATLAB cond()函数:求条件数(附带实例)
在线性代数中,矩阵 A 的条件数用来度量线性方程 Ax=b 的解对 b 中的误差或不确定性的敏感度,其对应的数学定义是:
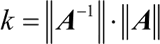
根据基础的数学知识,矩阵的条件数总是大于或等于 1。其中,正交矩阵的条件数为 1,奇异矩阵的条件数为 ∞,而病态矩阵的条件数则比较大。
依据条件数的定义,方程解的相对误差可以由下面的不等式来估计。
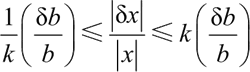
在 MATLAB 中,利用 cond() 函数可以求矩阵 X 的条件数,其调用格式如下:
【实例】以 MATLAB 产生的 Magic 矩阵和 Hilbert 矩阵为例,使用矩阵的条件数来分析对应的线性方程解的精度。在命令行窗口中输入以下语句,并查看输出结果。
1) 数值求解。
2) 修改矩阵,重新计算求解的精度。在命令行窗口中输入以下语句,并查看输出结果:
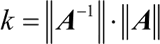
根据基础的数学知识,矩阵的条件数总是大于或等于 1。其中,正交矩阵的条件数为 1,奇异矩阵的条件数为 ∞,而病态矩阵的条件数则比较大。
依据条件数的定义,方程解的相对误差可以由下面的不等式来估计。
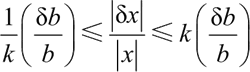
在 MATLAB 中,利用 cond() 函数可以求矩阵 X 的条件数,其调用格式如下:
C = cond(A) % 返回 2-范数逆运算的条件数,等于 A 的最大奇异值与最小奇异值之比 C = cond(A,p) % 返回 p-范数条件数,其中 p 可以是 1、2、Inf 或 'fro'
【实例】以 MATLAB 产生的 Magic 矩阵和 Hilbert 矩阵为例,使用矩阵的条件数来分析对应的线性方程解的精度。在命令行窗口中输入以下语句,并查看输出结果。
1) 数值求解。
>> clear
>> M = magic(3); % 创建 3×3 的 Magic 矩阵
>> b = ones(3,1); % 创建一个 3×1 的全为 1 的列向量 b
>> x = M\b; % 使用左除法求线性方程组 M*x=b 的近似解
>> xinv = inv(M)*b; % 通过矩阵求逆法求线性方程组 M*x=b 的解
>> ndb = norm(M*x-b); % 计算解的残差 (M*x-b) 的范数
>> nb = norm(b); % 计算向量 b 的范数
>> ndx = norm(x-xinv); % 计算 x 和 xinv 之间差值的范数
>> nx = norm(x); % 计算近似解 x 的范数
>> chu = ndx/nx % 计算相对误差(解的相对误差)
chu =
1.6997e-16
>> cha = cond(M) % 计算矩阵 M 的条件数,代表最大可能的近似相对误差
cha =
4.3301
>> chaa = cha*eps % 计算最大可能的相对误差,cha 为条件数,eps 为机器精度
chaa =
9.6148e-16
>> chaau = cha*ndb/nb % 用残差的比例计算最大可能的相对误差
chaau =
0
由结果可以看出,该矩阵的条件数为 4.3301,这种情况下引起的计算误差是很小的,其误差完全可以接受。2) 修改矩阵,重新计算求解的精度。在命令行窗口中输入以下语句,并查看输出结果:
>> clear
>> M = hilb(12); % 创建 12×12 的 Hilbert 矩阵
>> b = ones(12,1); % 创建一个 12×1 的全为 1 的列向量 b
>> x = M\b; % 使用左除法求线性方程组 M*x=b 的近似解
% 警告:矩阵接近奇异值,或者缩放不良。结果可能不准确。RCOND = 2.609829e-17
>> xinv = invhilb(12)*b; % 使用 Hilbert 矩阵的逆矩阵求精确解 xinv
>> ndb = norm(M*x-b); % 计算解的残差 (M*x-b) 的范数
>> nb = norm(b); % 计算向量 b 的范数
>> nbx = norm(x-xinv); % 计算近似解与精确解之间差值的范数
>> nx = norm(x); % 计算近似解 x 的范数
>> chu = nbx/nx % 计算相对误差(解的相对误差)
chu =
0.0733
>> cha = cond(M) % 计算矩阵 M 的条件数,代表最大可能的近似相对误差
cha =
1.6212e+16
>> chaa = cha*eps % 计算最大可能的相对误差,cha 为条件数,eps 为机器精度
chaa =
3.5997
>> chaau = cha*ndb/nb % 通过残差计算最大可能的相对误差
chaau =
3.3642e+07
由结果可以看出,该矩阵的条件数为 1.6212e+16,该矩阵在数学理论中是高度病态的,这样会造成比较大的计算误差。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: