C++解决01背包问题(附带示例)
背包问题是一类经典的组合优化问题。在该问题中,给定一组物品,每个物品具有特定的重量和价值。在总重量受限的情况下,需要选择若干物品,使得总价值达到最大。
假设有 n 件物品和一个容量为 m 的背包,给出 i 件物品的重量和价值 value,求解让装入背包物品的总重量不超过背包容量 m,如何选择物品,使背包内物品的总价值 V 最大。
这是最简单的背包问题,它的特点是每件物品只能选择“放入”或“不放入”两种状态,因此也成为“0-1背包”问题。
在 0-1 背包问题中,核心在于计算两个状态:对于第 i 个物品,选择“放入”或“不放入”。
【实例】采药问题。辰辰是一个极具潜力、天资聪颖的孩子,梦想成为世界上最伟大的医师。为了实现这个梦想,他决定拜附近最有威望的医师为师。为了考察他的资质,这位医师给辰辰出了一道难题。医师把辰辰带到一个遍布草药的山洞,对他说:“孩子,这个山洞里有一些不同种类的草药,采摘每一株草药需要一定的时间,而每一株草药也有其独特的价值。我会给你一段固定的时间,在这段时间内,你可以尽量采集草药。如果你是一个聪明的孩子,应该能够使采集到的草药的总价值最大。”如果你是辰辰,能完成这个任务吗?
输入格式:
输出格式:
可能有多组测试数据,对于每组数据:输出只包括一行,这一行只包含一个整数,表示在规定的时间内可以采到的草药的最大总价值。
样例输入:
样例输出:
解题思路:定义状态 dp[i][j] 表示采到第 i 株草药为止,在总时间不超过 j 的情况下,草药的最大总价值。
需要注意的是,状态定义中的“不超过”意味着 dp[n][m] 包括总时间为 1,2,…,n 的所有情况。如果要求时间严格为 j,则需要将 dp 数组初始化为负无穷。
以下代码中用 f 表示动态规划数组 dp:
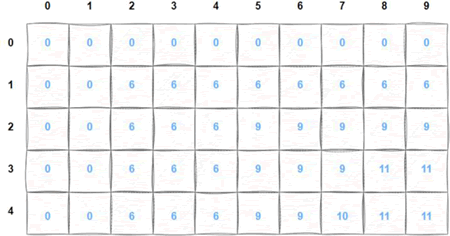
下图中的列代表空间,行代表物品,有一个背包容量为 9,有 4 件物品,占用体积分别是 2、3、6、5,对应的价值为 6、3、5、4。
由于动态规划中每次状态转移至依赖于上一行的状态,因此时间复杂度已不能再优化了,但空间复杂度仍可以再优化,这里我们采用滚动数组优化。
滚动数组优化的代码如下:
当然,对于这道题,还可以考虑采用搜索的方法进行求解。以下提供一段参考代码:
假设有 n 件物品和一个容量为 m 的背包,给出 i 件物品的重量和价值 value,求解让装入背包物品的总重量不超过背包容量 m,如何选择物品,使背包内物品的总价值 V 最大。
这是最简单的背包问题,它的特点是每件物品只能选择“放入”或“不放入”两种状态,因此也成为“0-1背包”问题。
在 0-1 背包问题中,核心在于计算两个状态:对于第 i 个物品,选择“放入”或“不放入”。
【实例】采药问题。辰辰是一个极具潜力、天资聪颖的孩子,梦想成为世界上最伟大的医师。为了实现这个梦想,他决定拜附近最有威望的医师为师。为了考察他的资质,这位医师给辰辰出了一道难题。医师把辰辰带到一个遍布草药的山洞,对他说:“孩子,这个山洞里有一些不同种类的草药,采摘每一株草药需要一定的时间,而每一株草药也有其独特的价值。我会给你一段固定的时间,在这段时间内,你可以尽量采集草药。如果你是一个聪明的孩子,应该能够使采集到的草药的总价值最大。”如果你是辰辰,能完成这个任务吗?
输入格式:
- 输入的第一行包含两个整数 T(1≤T≤1000)和 M(1≤M≤100),T 代表总共能够用来采药的时间,M 代表山洞中草药的种类数。
- 接下来的 M 行中,每行包括两个 1~100(包括 1 和 100)的整数,分别表示采摘某株草药所需的时间和该株草药的价值。
输出格式:
可能有多组测试数据,对于每组数据:输出只包括一行,这一行只包含一个整数,表示在规定的时间内可以采到的草药的最大总价值。
样例输入:
42 6 1 35 25 70 59 79 65 63 46 6 28 82 962 6 43 96 37 28 5 92 54 3 83 93 17 22
样例输出:
117 334
解题思路:定义状态 dp[i][j] 表示采到第 i 株草药为止,在总时间不超过 j 的情况下,草药的最大总价值。
需要注意的是,状态定义中的“不超过”意味着 dp[n][m] 包括总时间为 1,2,…,n 的所有情况。如果要求时间严格为 j,则需要将 dp 数组初始化为负无穷。
以下代码中用 f 表示动态规划数组 dp:
#include <bits/stdc++.h>
using namespace std;
int n, m;
// 定义物品数量 n 和背包容量 m(总时间)
int t[101], v[101];
// 定义草药的采摘时间 t 和价值数组 v
int f[101][1001];
// 定义动态规划数组 f,f[i][j] 表示前 i 种草药在时间 j 内的最大价值
int main() {
cin >> m >> n;
// 输入总时间和草药数量
for (int i = 1; i <= n; i++)
// 输入每株草药的采摘时间和价值
cin >> t[i] >> v[i];
for (int i = 1; i <= n; i++) { // 遍历每株草药
for (int j = 0; j <= m; j++) { // 遍历可用时间
if (j - t[i] >= 0) // 如果可以采摘当前草药
f[i][j] = max(f[i - 1][j], f[i - 1][j - t[i]] + v[i]); // 选择采摘或不采摘的最大价值
else
f[i][j] = f[i - 1][j]; // 否则只能选择不采摘
}
}
cout << f[n][m]; // 输出最大总价值
return 0;
}
其中,状态转移方程为 f[i][j]=max(f[i−1][j],f[i−1][j−t[i]]+v[i])。下图中的列代表空间,行代表物品,有一个背包容量为 9,有 4 件物品,占用体积分别是 2、3、6、5,对应的价值为 6、3、5、4。

由于动态规划中每次状态转移至依赖于上一行的状态,因此时间复杂度已不能再优化了,但空间复杂度仍可以再优化,这里我们采用滚动数组优化。
滚动数组优化的代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010; // 定义数组最大长度
int n, m;
// 定义整数 n 和 m,分别表示物品数量和背包容量
int v[N], w[N];
// 定义整数数组 v 和 w,分别表示物品的价值和重量(对应采摘草药的价值和所需时间)
int f[N];
// 定义滚动数组 f,用于存储动态规划的结果(即最大总价值)
int main() {
cin >> m >> n; // 输入时间和草药种类数
for (int i = 1; i <= n; i++) // 输入采摘价值和时间
cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++) { // 遍历所有草药
// 从大到小(逆序)遍历时间
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]); // 更新 f[j] 为不放入或放入第 i 个草药的最大总价值
}
cout << f[m]; // 输出最大总价值
return 0;
}
我们注意到,内层循环是从大到小枚举空间的。从正确性的角度来看,这种方式是必需的。原因在于,我们需要在给定容量 j 下,决定是否放入当前物品 i。当枚举到 j 时,数组 f[1]~f[j-1] 仍保留上一层的状态,而 f[j+1]~f[m] 都已经是当前层的状态更新结果。由于当前状态只能从上一层状态转移而来,并且 f[j] 的更新状态由 f[j-v[i]] 转移过来,因此枚举顺序必须从右到左,才能保证“新状态的左侧是旧状态,新状态从旧状态转移过来”。同样的道理,如果状态从右侧转移过来,那就只能从左到右枚举。当然,对于这道题,还可以考虑采用搜索的方法进行求解。以下提供一段参考代码:
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f; // 修正:原常量写法,保证足够大
int n, t; // n 物品件数,t 背包容量
int c[103], v[103]; // c[i] 费用/体积,v[i] 价值
int mem[103][1003]; // 记忆化数组,-1 表示未访问
int dfs(int pos, int l) {
if (mem[pos][l] != -1)
return mem[pos][l]; // 已经访问过的状态,直接返回之前记录的值
if (pos == n + 1)
return mem[pos][l] = 0; // 边界:无物品可选,价值为 0
int dfs1, dfs2 = -INF;
dfs1 = dfs(pos + 1, l); // 不选当前物品
if (l >= c[pos])
dfs2 = dfs(pos + 1, l - c[pos]) + v[pos]; // 选当前物品,状态转移
return mem[pos][l] = max(dfs1, dfs2); // 记录并返回最优值
}
int main() {
memset(mem, -1, sizeof(mem)); // 初始化记忆化数组为 -1
cin >> t >> n; // 输入背包容量与物品件数
for (int i = 1; i <= n; i++)
cin >> c[i] >> v[i]; // 输入每件物品的费用和价值
cout << dfs(1, t) << endl; // 从第 1 件物品、剩余容量 t 开始递归
return 0;
}
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: