C++递归解决汉诺塔问题(附带源码和解析)
有 3 个立柱垂直矗立在地面,给这 3 个立柱分别命名为 A、B、C。开始时立柱 A 上有 64 个圆盘,大小不一,并且按从小到大的顺序依次摆放在立柱 A 上。现在要将立柱 A 上的 64 个圆盘移到立柱 C 上,并且每次只允许移动一个圆盘,在移动过程中始终保持大盘在下,小盘在上。
64 个圆盘的移动过于复杂,因此我们先来简化一下问题。假设要移动的圆盘只有 4 个,它们初始都位于立柱 A 上,圆盘按由上到下的顺序分别命名为 a、b、c、d,如下图所示。
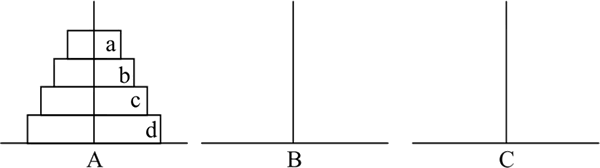
图 1 圆盘初始状态
首先,将 a、b 两个圆盘移动到立柱 C 上。移动过程需要借助立柱 B,移动顺序是 a->B,b->C,a->C,移动次数为 3 次。移动结果如下图所示。
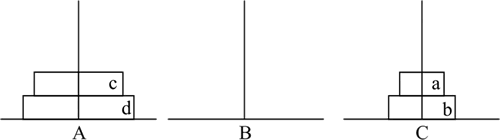
图 2 移动两个圆盘到立柱C
接下来,将 a、b、c 这 3 个圆盘移动到立柱 B 上。移动顺序是 c->B,a->A,b->B,a->B,移动次数为 4 次,移动结果如下图所示。
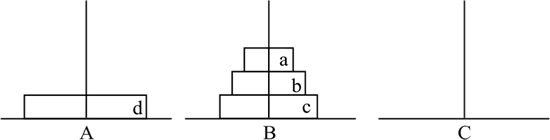
图 3 移动 3 个圆盘到立柱 B
最后,将 4 个圆盘都移动到立柱 C 上。移动顺序是
先来总结一下移动规律:
以此类推,当有 n 个圆盘时,要将它们移动到指定立柱,需要移动 2^n-1次。
继续思考,移动过程中,如果将 a、b、c 这 3 个圆盘看成一个整体,则移动 4 个圆盘的过程和移动 2 个圆盘一样。同理,将 a、b 2 个圆盘看成一个整体,则移动 3 个圆盘的过程也像是在移动 2 个圆盘。因此,可以使用递归的思路解决 n 个圆盘的移动问题,整个移动过程分为 3 步:
现在我们试着用上述递归思路编写程序,具体代码如下:
64 个圆盘的移动过于复杂,因此我们先来简化一下问题。假设要移动的圆盘只有 4 个,它们初始都位于立柱 A 上,圆盘按由上到下的顺序分别命名为 a、b、c、d,如下图所示。

图 1 圆盘初始状态
首先,将 a、b 两个圆盘移动到立柱 C 上。移动过程需要借助立柱 B,移动顺序是 a->B,b->C,a->C,移动次数为 3 次。移动结果如下图所示。

图 2 移动两个圆盘到立柱C
接下来,将 a、b、c 这 3 个圆盘移动到立柱 B 上。移动顺序是 c->B,a->A,b->B,a->B,移动次数为 4 次,移动结果如下图所示。

图 3 移动 3 个圆盘到立柱 B
最后,将 4 个圆盘都移动到立柱 C 上。移动顺序是
d->C,a->C,b->A,a->A,c->C,a->B,b->C,a->C。先来总结一下移动规律:
- 将 2 个圆盘移动到指定立柱,需要移动 3 次。例如,将 a、b 圆盘由立柱 A 移到立柱 C 上,移动顺序为 a->B,b->C,a->C。
- 将 3 个圆盘移动到指定立柱,需要移动 7 次。例如,将 a、b、c 圆盘由立柱 A 移到立柱 B 上,移动顺序为 a->B,b->C,a->C,c->B,a->A,b->B,a->B。其中,前 3 次重复的是将 2 个圆盘移动到指定立柱的操作,后 4 次是将第 3 个圆盘移动到指定立柱的操作。
- 将 4 个圆盘移动到指定立柱,需要移动 15 次。同样,前 7 次重复的是将 3 个圆盘移动到指定立柱的操作,后 8 次是将第 4 个圆盘移动到指定立柱的操作。
以此类推,当有 n 个圆盘时,要将它们移动到指定立柱,需要移动 2^n-1次。
继续思考,移动过程中,如果将 a、b、c 这 3 个圆盘看成一个整体,则移动 4 个圆盘的过程和移动 2 个圆盘一样。同理,将 a、b 2 个圆盘看成一个整体,则移动 3 个圆盘的过程也像是在移动 2 个圆盘。因此,可以使用递归的思路解决 n 个圆盘的移动问题,整个移动过程分为 3 步:
- 把立柱 A 上的 n-1 个圆盘移动到立柱 B 上;
- 把立柱 A 上的 1 个圆盘移动到立柱 C 上;
- 把立柱 B 上的 n-1 个圆盘移动到立柱 C 上。
现在我们试着用上述递归思路编写程序,具体代码如下:
#include <iostream>
using namespace std;
long lCount;
void move(int n, char a, char b, char c) //定义 move()函数,将 n 个圆盘从立柱 a 移到立柱 c
{
if(n==1) //如果只有 1 个圆盘
cout << "Times:" << ++lCount << ' ' << a << "->" << c << endl;
else //如果有多个圆盘
{
move(n-1, a, c, b); //递归调用 move()函数
cout << "Times:" << ++lCount << ' ' << a << "->" << c << endl;
move(n-1, b, a, c); //递归调用 move()函数
}
}
int main()
{
int n;
lCount=0; //lCount 表示移动次数
cout << "please input a number" << endl;
cin >> n; //输入圆盘数量
move(n, 'A', 'B', 'C'); //调用 move()函数,将 n 个圆盘从立柱 A 移到立柱 C
}
程序运行结果为:
please input a number 3 Times:1 A->C Times:2 A->B Times:3 C->B Times:4 A->C Times:5 B->A Times:6 B->C Times:7 A->C这里输入数字 3,表示要移动 3 个圆盘,程序将输出 3 个圆盘的移动步骤,与我们前面分析的移动过程完全一致。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: