回溯法解决n皇后问题(图文并茂,C++实现)
在 n×n 的方格棋盘上放置 n 个皇后,使得它们不相互攻击(即任意两个皇后都不允许同行、同列、同斜线)。求有多少种放置方案。
输入:输入包含多个测试用例,每个测试用例都为一个正整数n(n≤10),表示在 n×n 的方格棋盘上放置 n 个皇后,若 n=0,则表示结束。
输出:对于每个测试用例,都单行输出一个正整数,表示有多少种放置方案。

如下图所示,n 皇后问题是在 n×n 的棋盘上放置彼此不受攻击的 n 个皇后,任意两个皇后都不允许同行、同列、同斜线。若在第 i 行第 j 列放置一个皇后,则在第 i 行的其他位置(同行)、第 j 列的其他位置(同列)、同一斜线上的其他位置,都不能再放置皇后。
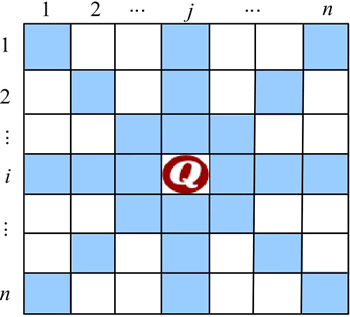
不能杂乱无章地尝试每个位置,需要有策略地求解,在此以行序为主进行放置。
2) 解空间的组织结构。n 皇后问题的解空间是一棵 m(m=n)叉树,如下图所示:
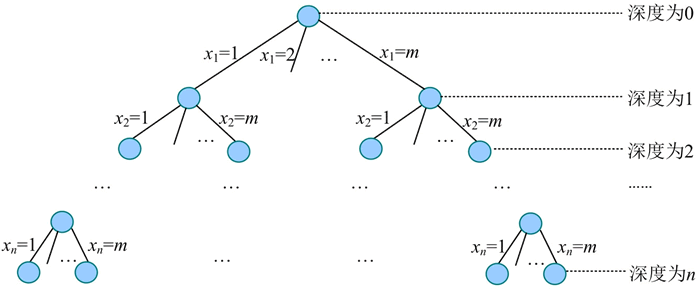
3) 搜索解空间
1) 开始搜索第 1 层(t=1)。扩展节点 1,判断 x1=1 是否满足约束条件,因为之前还未放置任何皇后,所以满足约束条件。令 x1=1,生成节点 2。
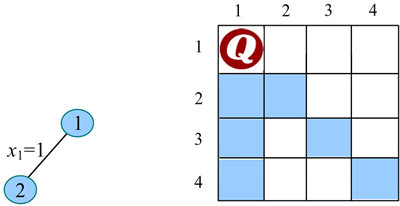
2) 扩展节点 2(t=2):
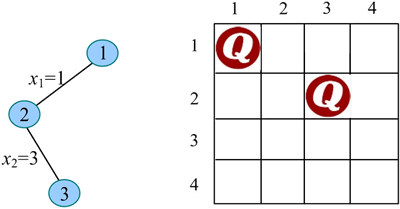
3) 扩展节点3(t=3):
已将节点 3 的所有孩子全部搜索完毕,回溯到节点 2。

4) 重新扩展节点 2(t=2)。x2=4 满足约束条件(与已放置的第 1 个皇后不同列、不同斜线),令 x2=4,生成节点 4。

5) 扩展节点 4(t=3):
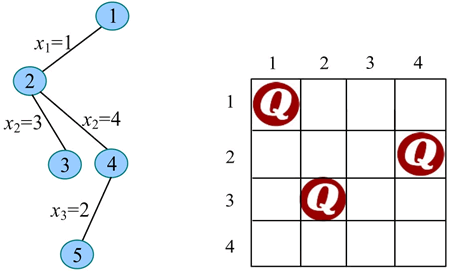
6) 扩展节点 5(t=4):
已将节点 5 的所有孩子全部搜索完毕,回溯到节点 4。
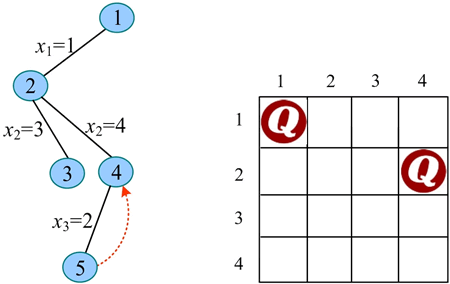
7) 继续扩展节点 4(t=3):
已将节点 4 的所有孩子全部搜索完毕,回溯到节点 2。已将节点 2的所有孩子全部搜索完毕,回溯到节点 1。
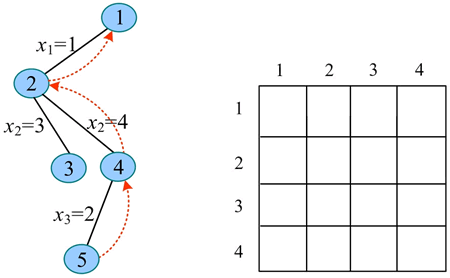
8) 继续扩展节点1(t=1)。x1=2 满足约束条件(之前未放置皇后),令 x1=2,生成节点 6。

9) 扩展节点 6(t=2):
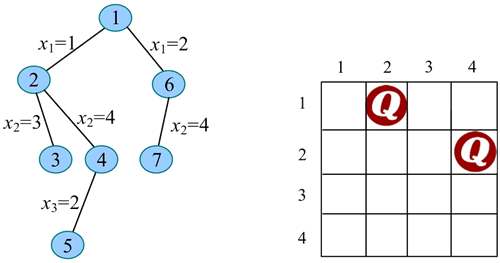
10) 扩展节点 7(t=3)。x3=1 满足约束条件(与已放置的第 1、2 个皇后不同列、不同斜线),令 x3=1,生成节点 8。
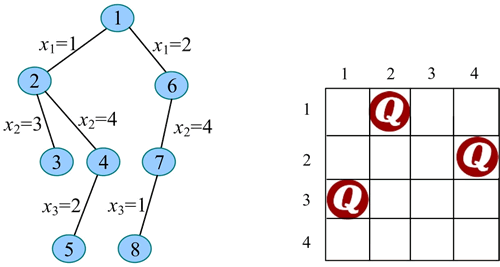
11) 扩展节点 8(t=4):
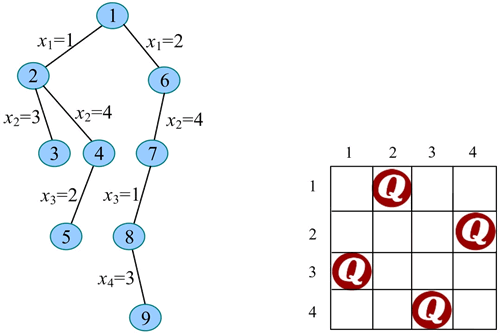
12) 扩展节点 9(t=5)。此时 t>n,找到一个可行解,用数组 bestx[] 保存当前可行解 {2,4,1,3}。回溯到节点 8。
13) 继续扩展节点 8(t=4)。x4=4 不满足约束条件(与已放置的第 2 个皇后同列)。已将节点 8 的所有孩子全部搜索完毕,回溯到节点 7。
14) 继续扩展节点 7(t=3):
已将节点 7 的所有孩子全部搜索完毕,回溯到节点 6。已将节点 6 的所有孩子全部搜索完毕,回溯到节点 1。
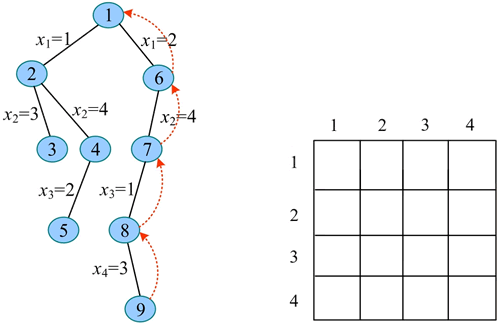
15) 继续扩展节点 1(t=1)。x1=3 满足约束条件(之前未放置皇后),令 x1=3,生成节点 10。
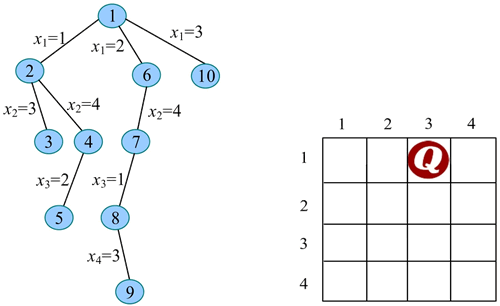
16) 扩展节点 10(t=2)。x2=1 满足约束条件(与已放置的第 1 个皇后不同列、不同斜线),令 x2=1,生成节点 11。
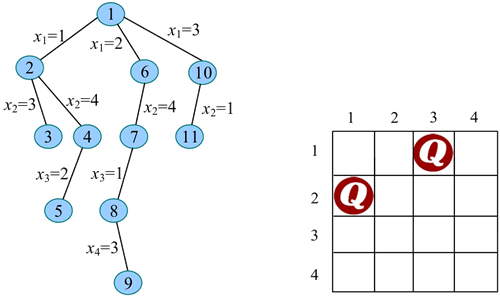
17) 扩展节点 11(t=3):
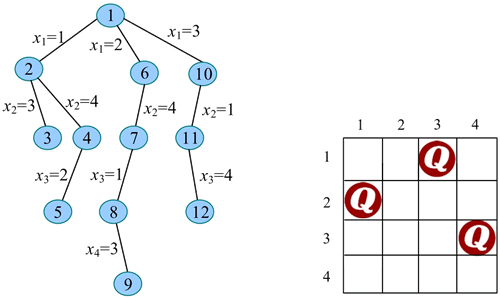
18) 扩展节点 12(t=4)。x4=1 不满足约束条件(与已放置的第 2 个皇后同列);x4=2 满足约束条件(与已放置的第 1、2、3 个皇后不同列、不同斜线),令 x4=2,生成节点 13。
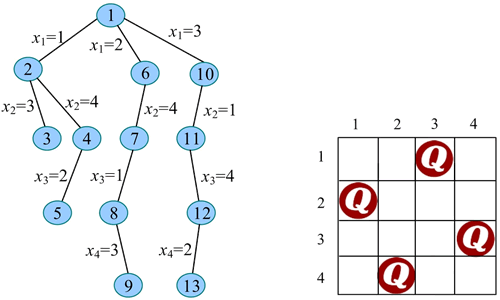
19) 扩展节点 13(t=5)。此时 t>n,找到一个可行解,用数组 bestx[] 保存当前可行解 {3,1,4,2}。回溯到节点 12。
20) 继续扩展节点 12(t=4):
已将节点 12 的所有孩子全部搜索完毕,回溯到节点 11。已将节点 11 的所有孩子全部搜索完毕,回溯到节点 10。
21) 继续扩展节点 10(t=2):
已将节点 10 的所有孩子全部搜索完毕,回溯到节点 1。
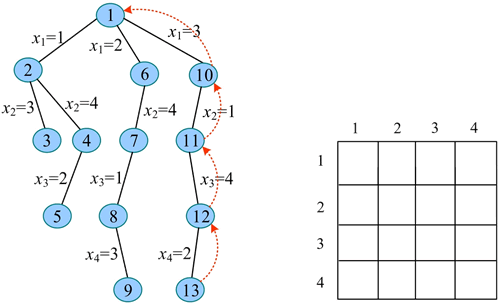
22) 继续扩展节点 1(t=1)。x1=4 满足约束条件(之前未放置皇后),令 x1=4,生成节点 14。
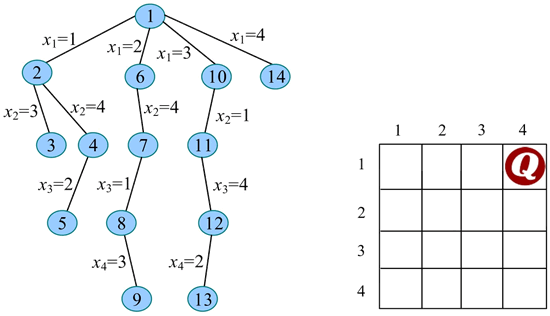
23) 扩展节点 14(t=2)。x2=1 满足约束条件(与已放置的第 1 个皇后不同列、不同斜线),令 x2=1,生成节点 15。
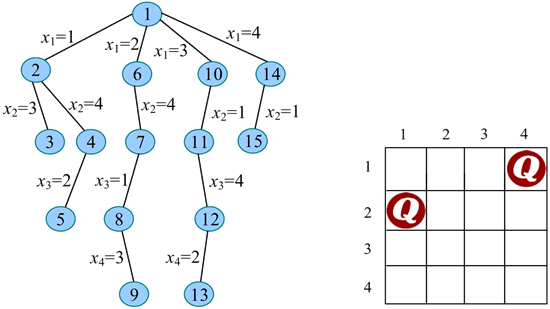
24) 扩展节点 15(t=3):
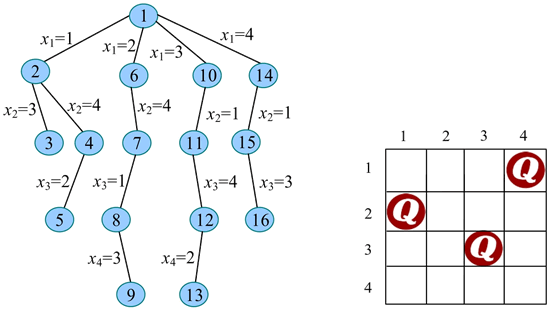
25) 扩展节点 16(t=4):
已将节点 16 的所有孩子全部搜索完毕,回溯到节点 15。
26) 继续扩展节点 15(t=3)。x3=4 不满足约束条件(与已放置的第 1 个皇后同列)。已将节点 15 的所有孩子全部搜索完毕,回溯到节点 14。
27) 继续扩展节点 14(t=2)。x2=2 满足约束条件(与已放置的第 1 个皇后不同列、不同斜线),令 x2=2,生成节点 17。

28) 扩展节点 17(t=3):
已将节点17的所有孩子全部搜索完毕,回溯到节点14。
29) 继续扩展节点 14(t=2)。x3=3 不满足约束条件(与已放置的第 2 个皇后同斜线);x3=4 不满足约束条件(与已放置的第 1 个皇后同列)。已将节点 14 的所有孩子全部搜索完毕,回溯到节点 1。
30) 已将节点 1 的所有孩子全部搜索完毕,算法结束。
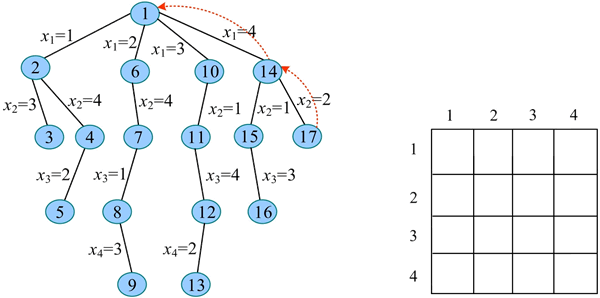
2) 按约束条件搜索求解。若 t>n,则表示找到一个可行解,记录最优值和最优解并返回。否则分别判断 i=1…n 个分支,x[t]=i:判断每个分支是否满足约束条件,若满足,则进入下一层 Backtrack(t+1),否则考查下一个分支。
3) 打表法预处理。本题最多有 10 个皇后,但是有大量测试用例要查询,需要采用打表法做预处理,先解出所有答案并将其存储起来,在每次查询时直接输出答案。
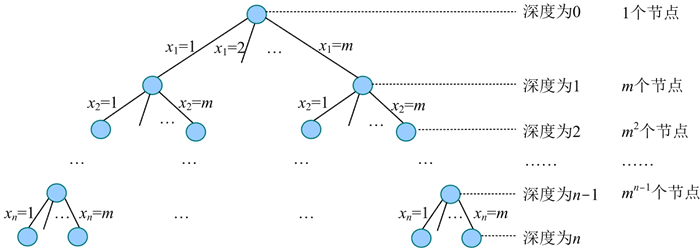
除了最后一层,有 1+n+n^2+…+n^(n-1)=(n^n-1)/(n-1)≈ n^(n-1) 个节点需要扩展,每个节点都要扩展 n 个分支,总分支数为 n^n,在每个分支都需要判断约束函数,判断约束条件的时间复杂度为 O(n),总时间复杂度为 O(n^(n+1))。在叶子处输出当前最优解的时间复杂度为 O(n),在最坏情况下会搜索到所有叶子,叶子数为 n^n,总时间复杂度为 O(n^(n+1))。所以,总时间复杂度为 O(n^(n+1))。
空间复杂度:使用数组 x[] 保存该最长路径并将其作为可行解,空间复杂度为 O(n)。
n 皇后问题要求每个皇后都不同行、不同列、不同斜线。上图所示的解空间显约束为不同行,隐约束为不同列、不同斜线。4 皇后问题,显约束为不同行的解空间树如下图所示。
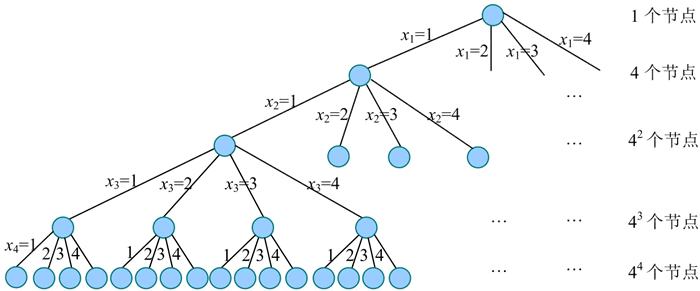
显约束可以控制解空间的大小,隐约束可以在搜索过程中判定可行解或最优解。若把显约束定为不同行、不同列,把隐约束定为不同斜线,则解空间是怎样的呢?
例如,当 x1=1 时,x2 就不能再等于 1,因为这样就同列了。若 x1=1,x2=2,x3 就不能再等于 1、2。也就是说,xt 的值不能与前 t-1 个解的值相同。每层节点产生的孩子数都比上一层少 1。4 皇后问题,显约束为不同行、不同列的解空间树如下图所示。
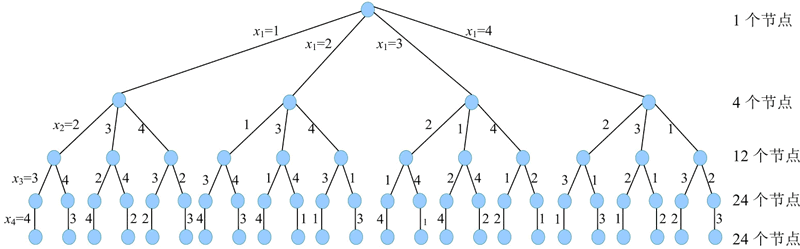
可以清楚地看到解空间变小许多,通过仔细观察就会发现,上图中从根到叶子的每个可能解都是一个排列,该解空间树是一棵排列树。使用排列树求解 n 皇后问题的代码如下。
输入:输入包含多个测试用例,每个测试用例都为一个正整数n(n≤10),表示在 n×n 的方格棋盘上放置 n 个皇后,若 n=0,则表示结束。
输出:对于每个测试用例,都单行输出一个正整数,表示有多少种放置方案。

如下图所示,n 皇后问题是在 n×n 的棋盘上放置彼此不受攻击的 n 个皇后,任意两个皇后都不允许同行、同列、同斜线。若在第 i 行第 j 列放置一个皇后,则在第 i 行的其他位置(同行)、第 j 列的其他位置(同列)、同一斜线上的其他位置,都不能再放置皇后。

不能杂乱无章地尝试每个位置,需要有策略地求解,在此以行序为主进行放置。
- 在第 1 行第 1 列放置第 1 个皇后。
- 在第 2 行放置第 2 个皇后。第 2 个皇后的位置不能与第 1 个皇后同列、同斜线,不用再判断是否同行,因为每行只放置一个皇后,所以肯定不同行。
- ……
- 在第 n 行放置第 n 个皇后,第 n 个皇后的位置不能与前 n-1 个皇后同列、同斜线。
算法设计
1) 定义问题的解空间。解的组织形式为 n 元组:{x1,x2,…,xi,…,xn},xi 表示第 i 个皇后被放置在第 i 行第 xi 列,xi 的取值为 1,2,…,n。例如 x2=5,表示第 2 个皇后被放置在第 2 行第 5 列。2) 解空间的组织结构。n 皇后问题的解空间是一棵 m(m=n)叉树,如下图所示:

3) 搜索解空间
- 约束条件。在第 t 行放置第 t 个皇后时,第 t 个皇后不能与前 t-1 个皇后同列、同斜线。第 i 个皇后与第 j 个皇后不同列(xi!=xj),而且不同斜线(|i-j|!=|xi-xj|)。
- 限界条件。该问题不存在放置方案好坏的情况,不需要设置限界条件。
- 搜索过程。从根开始,沿着节点的第 1 个分支搜索,若满足约束条件,则进入下一层继续搜索;若不满足约束条件,则换下一个分支继续搜索;若已将当前节点的分支节点全部搜索完毕,则回溯到最近的上层节点,继续搜索。直到将所有节点全部搜索完毕时为止。
完美图解
例如,在 4×4 的棋盘上放置 4 个皇后,使其彼此不受攻击。1) 开始搜索第 1 层(t=1)。扩展节点 1,判断 x1=1 是否满足约束条件,因为之前还未放置任何皇后,所以满足约束条件。令 x1=1,生成节点 2。

2) 扩展节点 2(t=2):
- x2=1 不满足约束条件(与已放置的第 1 个皇后同列);
- x2=2 不满足约束条件(与已放置的第 1 个皇后同斜线);
- x2=3 满足约束条件(与已放置的皇后不同列、不同斜线),令 x2=3,生成节点 3。

3) 扩展节点3(t=3):
- x3=1 不满足约束条件(与已放置的第 1 个皇后同列);
- x3=2 不满足约束条件(与已放置的第 2 个皇后同斜线);
- x2=3 不满足约束条件(与已放置的第 2 个皇后同列);
- x3=4 不满足约束条件(与已放置的第 2 个皇后同斜线)。
已将节点 3 的所有孩子全部搜索完毕,回溯到节点 2。

4) 重新扩展节点 2(t=2)。x2=4 满足约束条件(与已放置的第 1 个皇后不同列、不同斜线),令 x2=4,生成节点 4。

5) 扩展节点 4(t=3):
- x3=1 不满足约束条件(与已放置的第 1 个皇后同列);
- x3=2 满足约束条件(与已放置的第 1、2 个皇后不同列、不同斜线),令 x3=2,生成节点 5。

6) 扩展节点 5(t=4):
- x4=1 不满足约束条件(与已放置的第 1 个皇后同列);
- x4=2 不满足约束条件(与已放置的第 3 个皇后同列);
- x4=3 不满足约束条件(与已放置的第 3 个皇后同斜线);
- x4=4 不满足约束条件(与已放置的第 2 个皇后同列)。
已将节点 5 的所有孩子全部搜索完毕,回溯到节点 4。

7) 继续扩展节点 4(t=3):
- x3=3 不满足约束条件(与已放置的第 2 个皇后同斜线);
- x3=4 不满足约束条件(与已放置的第 2 个皇后同列)。
已将节点 4 的所有孩子全部搜索完毕,回溯到节点 2。已将节点 2的所有孩子全部搜索完毕,回溯到节点 1。

8) 继续扩展节点1(t=1)。x1=2 满足约束条件(之前未放置皇后),令 x1=2,生成节点 6。

9) 扩展节点 6(t=2):
- x2=1 不满足约束条件(与已放置的第 1 个皇后同斜线);
- x2=2 不满足约束条件(与已放置的第 1 个皇后同列);
- x2=3 不满足约束条件(与已放置的第 1 个皇后同斜线);
- x2=4 满足约束条件(与已放置的第 1 个皇后不同列、不同斜线),令 x2=4,生成节点 7。

10) 扩展节点 7(t=3)。x3=1 满足约束条件(与已放置的第 1、2 个皇后不同列、不同斜线),令 x3=1,生成节点 8。

11) 扩展节点 8(t=4):
- x4=1 不满足约束条件(与已放置的第 3 个皇后同列);
- x4=2 不满足约束条件(与已放置的第 1 个皇后同列);
- x4=3 满足约束条件(与已放置的第 1、2、3 个皇后不同列、不同斜线),令 x4=3,生成节点 9。

12) 扩展节点 9(t=5)。此时 t>n,找到一个可行解,用数组 bestx[] 保存当前可行解 {2,4,1,3}。回溯到节点 8。
13) 继续扩展节点 8(t=4)。x4=4 不满足约束条件(与已放置的第 2 个皇后同列)。已将节点 8 的所有孩子全部搜索完毕,回溯到节点 7。
14) 继续扩展节点 7(t=3):
- x3=2 不满足约束条件(与已放置的第 1 个皇后同列);
- x3=3 不满足约束条件(与已放置的第 2 个皇后同斜线);
- x3=4 不满足约束条件(与已放置的第 2 个皇后同列)。
已将节点 7 的所有孩子全部搜索完毕,回溯到节点 6。已将节点 6 的所有孩子全部搜索完毕,回溯到节点 1。

15) 继续扩展节点 1(t=1)。x1=3 满足约束条件(之前未放置皇后),令 x1=3,生成节点 10。

16) 扩展节点 10(t=2)。x2=1 满足约束条件(与已放置的第 1 个皇后不同列、不同斜线),令 x2=1,生成节点 11。

17) 扩展节点 11(t=3):
- x3=1 不满足约束条件(与已放置的第 2 个皇后同列);
- x3=2 不满足约束条件(与已放置的第 2 个皇后同斜线);
- x3=3 不满足约束条件(与已放置的第 1 个皇后同列);
- x3=4 满足约束条件(与已放置的第 1、2 个皇后不同列、不同斜线),令 x3=4,生成节点 12。

18) 扩展节点 12(t=4)。x4=1 不满足约束条件(与已放置的第 2 个皇后同列);x4=2 满足约束条件(与已放置的第 1、2、3 个皇后不同列、不同斜线),令 x4=2,生成节点 13。

19) 扩展节点 13(t=5)。此时 t>n,找到一个可行解,用数组 bestx[] 保存当前可行解 {3,1,4,2}。回溯到节点 12。
20) 继续扩展节点 12(t=4):
- x4=3 不满足约束条件(与已放置的第 1 个皇后同列);
- x4=4 不满足约束条件(与已放置的第 3 个皇后同列)。
已将节点 12 的所有孩子全部搜索完毕,回溯到节点 11。已将节点 11 的所有孩子全部搜索完毕,回溯到节点 10。
21) 继续扩展节点 10(t=2):
- x2=2 不满足约束条件(与已放置的第 1 个皇后同斜线);
- x2=3 不满足约束条件(与已放置的第 1 个皇后同列);
- x2=4 不满足约束条件(与已放置的第 1 个皇后同斜线)。
已将节点 10 的所有孩子全部搜索完毕,回溯到节点 1。

22) 继续扩展节点 1(t=1)。x1=4 满足约束条件(之前未放置皇后),令 x1=4,生成节点 14。

23) 扩展节点 14(t=2)。x2=1 满足约束条件(与已放置的第 1 个皇后不同列、不同斜线),令 x2=1,生成节点 15。

24) 扩展节点 15(t=3):
- x3=1 不满足约束条件(与已放置的第 2 个皇后同列);
- x3=2 不满足约束条件(与已放置的第 2 个皇后同斜线);
- x3=3 满足约束条件(与已放置的第 1、2 个皇后不同列、不同斜线),令 x3=3,生成节点 16。

25) 扩展节点 16(t=4):
- x4=1 不满足约束条件(与已放置的第 2 个皇后同列);
- x4=2 不满足约束条件(与已放置的第 3 个皇后同斜线);
- x4=3 不满足约束条件(与已放置的第 3 个皇后同列);
- x4=4 不满足约束条件(与已放置的第1个皇后同列)。
已将节点 16 的所有孩子全部搜索完毕,回溯到节点 15。
26) 继续扩展节点 15(t=3)。x3=4 不满足约束条件(与已放置的第 1 个皇后同列)。已将节点 15 的所有孩子全部搜索完毕,回溯到节点 14。
27) 继续扩展节点 14(t=2)。x2=2 满足约束条件(与已放置的第 1 个皇后不同列、不同斜线),令 x2=2,生成节点 17。

28) 扩展节点 17(t=3):
- x3=1 不满足约束条件(与已放置的第 2 个皇后同斜线);
- x3=2 不满足约束条件(与已放置的第 2 个皇后同列);
- x3=3 不满足约束条件(与已放置的第 2 个皇后同斜线);
- x3=4 不满足约束条件(与已放置的第 1 个皇后同列)。
已将节点17的所有孩子全部搜索完毕,回溯到节点14。
29) 继续扩展节点 14(t=2)。x3=3 不满足约束条件(与已放置的第 2 个皇后同斜线);x3=4 不满足约束条件(与已放置的第 1 个皇后同列)。已将节点 14 的所有孩子全部搜索完毕,回溯到节点 1。
30) 已将节点 1 的所有孩子全部搜索完毕,算法结束。

算法实现
1) 约束函数。在第 t 行放置第 t 个皇后时,第 t 个皇后不能与前 t-1 个已放置的皇后同列、同斜线:
x[t]=x[j] 表示第 t 个皇后与第 j 个皇后同列;
t-j=abs(x[t]-x[j]) 表示第 t 个皇后与第 j 个皇后同斜线。abs() 是求绝对值的函数,在使用该函数时要引入头文件 #include<cmath>。
bool check(int t) { //判断是否可以将第 t 个皇后放置在第 i 个位置,即 x[t]=i
for(int j=1;j<t;j++) { //判断是否与前面 t-1 个已放置的皇后冲突
if((x[t]==x[j]) || (t-j==abs(x[t]-x[j]))) //判断是否同列、同斜线
return false;
}
return true;
}
2) 按约束条件搜索求解。若 t>n,则表示找到一个可行解,记录最优值和最优解并返回。否则分别判断 i=1…n 个分支,x[t]=i:判断每个分支是否满足约束条件,若满足,则进入下一层 Backtrack(t+1),否则考查下一个分支。
void Backtrack(int t) {
if(t>n) { //若到达叶子,则表示已经找到了问题的一个解
ans++;
//for(int i=1;i<=n;i++) //输出可行解
// cout<<x[i]<<" ";
//cout<<endl;
}
else
for(int i=1;i<=n;i++) { //枚举n个分支
x[t]=i;
if(check(t))
Backtrack(t+1); //若不冲突,则进行下一行的搜索
}
}
3) 打表法预处理。本题最多有 10 个皇后,但是有大量测试用例要查询,需要采用打表法做预处理,先解出所有答案并将其存储起来,在每次查询时直接输出答案。
int main() {
for(int i=1;i<=10;i++) { //先做预处理,否则超时
ans=0;
n=i;
Backtrack(1);
s[i]=ans;
}
while(~scanf("%d",&n)) {
printf("%d\n",s[n]);
}
return 0;
}
算法分析
时间复杂度:在最坏情况下,解空间树如下图所示。
除了最后一层,有 1+n+n^2+…+n^(n-1)=(n^n-1)/(n-1)≈ n^(n-1) 个节点需要扩展,每个节点都要扩展 n 个分支,总分支数为 n^n,在每个分支都需要判断约束函数,判断约束条件的时间复杂度为 O(n),总时间复杂度为 O(n^(n+1))。在叶子处输出当前最优解的时间复杂度为 O(n),在最坏情况下会搜索到所有叶子,叶子数为 n^n,总时间复杂度为 O(n^(n+1))。所以,总时间复杂度为 O(n^(n+1))。
空间复杂度:使用数组 x[] 保存该最长路径并将其作为可行解,空间复杂度为 O(n)。
算法优化
在上面的求解过程中,由于解空间过于庞大,所以时间复杂度很高,算法效率低。解空间越小,算法效率越高。能不能把解空间缩小呢?n 皇后问题要求每个皇后都不同行、不同列、不同斜线。上图所示的解空间显约束为不同行,隐约束为不同列、不同斜线。4 皇后问题,显约束为不同行的解空间树如下图所示。

显约束可以控制解空间的大小,隐约束可以在搜索过程中判定可行解或最优解。若把显约束定为不同行、不同列,把隐约束定为不同斜线,则解空间是怎样的呢?
例如,当 x1=1 时,x2 就不能再等于 1,因为这样就同列了。若 x1=1,x2=2,x3 就不能再等于 1、2。也就是说,xt 的值不能与前 t-1 个解的值相同。每层节点产生的孩子数都比上一层少 1。4 皇后问题,显约束为不同行、不同列的解空间树如下图所示。

可以清楚地看到解空间变小许多,通过仔细观察就会发现,上图中从根到叶子的每个可能解都是一个排列,该解空间树是一棵排列树。使用排列树求解 n 皇后问题的代码如下。
for(int i=t;i<=n;i++) {
swap(x[t],x[i]); //通过交换得到全排列
if(check(t))
Backtrack(t+1);
swap(x[t],x[i]); //还原
}
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: