什么是回溯算法(图文并茂,新手必看)
回溯法(Backtracking)也称为试探法,是一种选优搜索法,该方法首先暂时放弃关于问题规模大小的限制,并将问题的候选解按照某种顺序逐一枚举和检验。
当发现当前的候选解不可能是解时,就选择下一个候选解;倘若当前候选解除不满足问题的规模要求外,满足所有其他要求,继续扩大当前候选解的规模,并继续向前试探。如果当前候选解满足包括问题规模在内的所有要求,该候选解就是问题的一个解。
在寻找解的过程中,放弃当前候选解,退回上一步重新选择候选解的过程就称为回溯。
回溯算法的思想就像走迷宫一样,在你不知道往哪个方向走时,可能会随机选择一个方向往前走,当你走到死胡同,即所有的路都走过但走不通时,就回退到前一个位置,重新选择另一条路向下走。
在如图 1 所示的迷宫中,当从入口处走到第 7 行第 1 列的位置时,发现所有方向都走不下去,就回退到第 6 行第 1 列的位置,此时若还走不通,则继续回退,直到第 5 行第 1 列的位置,会找到一条通路。
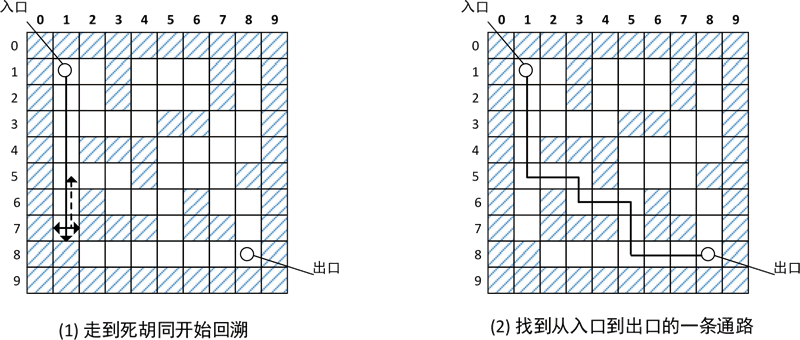
图 1 迷宫问题
利用回溯法解决问题有 3 个关键步骤:
当 n=3 时,解空间是由长度为 3 的向量组成的,每个向量的元素取值为 0 或 1,解空间为:

图 2 装载问题的解空间树
解向量 (1,1,1) 表示将重量为 18、25、25 的集装箱都装入轮船,总重量为 68。解向量 (0,1,1) 表示将重量为 25 和 25 的集装箱装入轮船,总重量为 50。
若已经生成一个结点或多个结点,而它的所有孩子结点还没有全部生成,则该结点称为活结点;扩展结点指的是当前正在生成孩子结点的活结点;死结点指的是不再继续扩展的结点或其孩子结点已经全部生成的结点。
当 c=50、W={18, 25, 25} 时,装载问题的搜索过程可以表示成一棵子集树,如下图所示:

图 3 装载问题的搜索过程
1) 初始时,根结点是唯一的活结点,也是当前的扩展结点,此时轮船的剩余容量为 cr=50,还未有集装箱装入轮船。
2) 从根结点 A 出发对左分支结点 B 进行扩展,若将第 1 个集装箱装入轮船,则有 cr=50-18=32,此时结点 B 为当前的扩展结点,结点 A 和结点 B 为活结点。
3) 从当前的扩展结点 B 继续沿深度方向扩展,若将第 2 个集装箱装入轮船,则有 cr=32-25=7,此时结点 D 为当前的扩展结点,结点 A、结点 B 和结点 D 为活结点。
4) 从当前的扩展结点 D 沿着左分支继续扩展,由于 cr<25,因此无法将第 3 个集装箱放入轮船,这是一个不可行的解,回溯到结点 D。
5) 结点 D 成为活结点,并成为当前的扩展结点,从结点 D 沿着右分支进行扩展,扩展到结点 I,即不将第 3 个集装箱装入轮船,此时有第 1 个和第 2 个集装箱装入轮船,得到一个可行解,解向量为 {1,1,0},装入轮船的集装箱总重量为 43。
6) 结点 I 不能再扩展,成为死结点,回溯到结点 D,结点 D 已无可扩展结点,成为死结点,回溯到结点 B。
7) 结点 B 成为当前的扩展结点,沿着结点 B 向右分支结点扩展,到达结点 E,结点 E 成为活结点,并成为当前的扩展结点,第 2 个集装箱不装入轮船,此时轮船上只有第 1 个集装箱,cr=32。
8) 沿着结点 E 往左分支扩展,结点 J 成为活结点,并成为当前的扩展结点,将第 3 个集装箱装入轮船,此时有 cr=32-25=7,第 1 个和第 3 个集装箱装入轮船,解向量为 {1,0,1},装入轮船的总重量为 43。
9) 结点 J 不可扩展,成为死结点,回溯到结点 E,结点 E 成为当前的扩展结点,沿着结点 E 向右分支扩展,到达结点 K,结点 K 为活结点,即第 3 个集装箱不装入轮船,此时 cr=32,只有第 1 个集装箱装入轮船,解向量为 {1,0,0},装入轮船的总重量为 18。
按照以上方式继续在解空间树上搜索,搜索完毕后,即可得到装载问题的最优解,最优解为 {0,1,1}。
一个旅行商要从 n 个城市的某一城市出发去往其他城市,每个城市经过且只经过一次,最后回到原来出发的城市。求在去往任何一个城市的所有路径中路径长度最短的一条。
为了方便描述该问题,可采用带权图表示 n 个城市之间的关系,顶点表示城市,顶点之间的权值表示城市之间的距离。例如,n=4 时的旅行商问题可用下图表示。
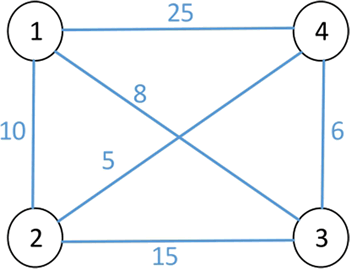
图 4 旅行商问题
图中的回路有 (1,2,3,4,1)、(1,2,4,3,1)、(1,3,2,4,1)、(1,4,2,3,1)、(1,3,4,2,1) 等,其中 (1,3,4,2,1) 的路径长度最短,其路径长度为 29。旅行商人所走过的可能路线其实是所有路径的排列组合,这些方案可绘制成一棵排列树,也是该问题的解空间树,如下图所示。
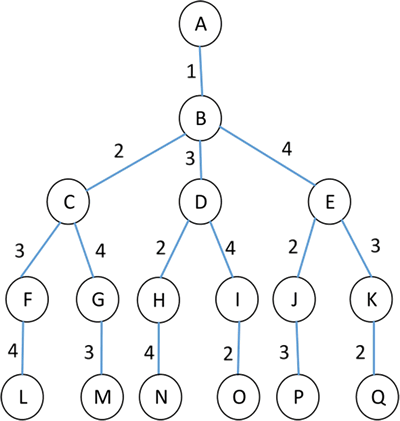
图 5 旅行商问题的解空间树
该树的深度为 5,两个结点之间的路径表示旅行商经过的城市。
利用回溯算法求解问题一般是先根据具体问题构造解空间树,也就是描述问题的解,然后在解空间树中从根结点出发搜索问题的解,直到遍历完整棵解空间树。
解空间树一般分为两种:子集树和排列树。当所给的问题是从 n 个元素的集合 S 中找出满足某种性质的子集时,相应的解空间树称为子集树。当所给问题是确定 n 个元素满足某种性质的排列时,相应的解空间树称为排列树。排列树通常有 n! 个叶子结点。因此,遍历排列树需要 O(n!) 的计算时间。
当发现当前的候选解不可能是解时,就选择下一个候选解;倘若当前候选解除不满足问题的规模要求外,满足所有其他要求,继续扩大当前候选解的规模,并继续向前试探。如果当前候选解满足包括问题规模在内的所有要求,该候选解就是问题的一个解。
在寻找解的过程中,放弃当前候选解,退回上一步重新选择候选解的过程就称为回溯。
回溯算法的基本思想
回溯算法在求解问题时,按照深度优先搜索策略对解空间树进行搜索,在搜索至解空间树中的任一结点时,先判断该结点是否包含问题的解:- 若包含问题的解,则沿着该分支继续进行深度优先搜索遍历;
- 否则,跳过该结点的分支沿着该结点向上一个结点回溯。
回溯算法的思想就像走迷宫一样,在你不知道往哪个方向走时,可能会随机选择一个方向往前走,当你走到死胡同,即所有的路都走过但走不通时,就回退到前一个位置,重新选择另一条路向下走。
在如图 1 所示的迷宫中,当从入口处走到第 7 行第 1 列的位置时,发现所有方向都走不下去,就回退到第 6 行第 1 列的位置,此时若还走不通,则继续回退,直到第 5 行第 1 列的位置,会找到一条通路。

图 1 迷宫问题
利用回溯法解决问题有 3 个关键步骤:
- 针对给定的问题,定义问题的解空间;
- 确定易于搜索的解空间结构;
- 以深度优先方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索。
1) 问题的解空间
问题的解空间至少包含一个最优解。例如,对于装载问题,若有 n 个集装箱要装上一艘载重量为 c 的轮船,其中集装箱 i 的重量为 wi,要求在不超过轮船载重量的前提下,将尽可能多的集装箱装上轮船。当 n=3 时,解空间是由长度为 3 的向量组成的,每个向量的元素取值为 0 或 1,解空间为:
{(0,0,0),(0,0,1),(0,1,0),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)}
其中,0 表示不装入轮船,1 表示装入轮船。若 c=50,W={18, 25, 25},则解空间可用一棵二叉树表示,左分支用 1 表示,右分支用 0 表示,如下图所示。
图 2 装载问题的解空间树
解向量 (1,1,1) 表示将重量为 18、25、25 的集装箱都装入轮船,总重量为 68。解向量 (0,1,1) 表示将重量为 25 和 25 的集装箱装入轮船,总重量为 50。
2) 算法的基本思想
在构造好解空间树之后,可以利用回溯算法对解空间树进行搜索,通过搜索求出问题的最优解。从解空间树的根结点出发,对解空间进行深度优先搜索遍历:- 初始时,根结点成为活结点,并成为当前的扩展结点,沿着扩展结点向纵深方向搜索,达到一个新的结点后,新的结点就成为活结点,并成为当前的扩展结点。
- 若当前的扩展结点不能继续向前搜索,则当前的扩展结点成为死结点,这时就会回溯到最近的活结点位置。
- 重复按以上方式搜索整个解空间树,直到程序结束。
若已经生成一个结点或多个结点,而它的所有孩子结点还没有全部生成,则该结点称为活结点;扩展结点指的是当前正在生成孩子结点的活结点;死结点指的是不再继续扩展的结点或其孩子结点已经全部生成的结点。
贪心算法实际应用
1) 解决装载问题
已知有 n 个集装箱(重量分别为 w1,w2,…,wn)和 1 艘轮船,轮船的载重量为 c,要求在不超过轮船载重量的前提下,将尽可能多的集装箱装入轮船。其中,第 i 个集装箱的重量为 wi。当 c=50、W={18, 25, 25} 时,装载问题的搜索过程可以表示成一棵子集树,如下图所示:

图 3 装载问题的搜索过程
1) 初始时,根结点是唯一的活结点,也是当前的扩展结点,此时轮船的剩余容量为 cr=50,还未有集装箱装入轮船。
2) 从根结点 A 出发对左分支结点 B 进行扩展,若将第 1 个集装箱装入轮船,则有 cr=50-18=32,此时结点 B 为当前的扩展结点,结点 A 和结点 B 为活结点。
3) 从当前的扩展结点 B 继续沿深度方向扩展,若将第 2 个集装箱装入轮船,则有 cr=32-25=7,此时结点 D 为当前的扩展结点,结点 A、结点 B 和结点 D 为活结点。
4) 从当前的扩展结点 D 沿着左分支继续扩展,由于 cr<25,因此无法将第 3 个集装箱放入轮船,这是一个不可行的解,回溯到结点 D。
5) 结点 D 成为活结点,并成为当前的扩展结点,从结点 D 沿着右分支进行扩展,扩展到结点 I,即不将第 3 个集装箱装入轮船,此时有第 1 个和第 2 个集装箱装入轮船,得到一个可行解,解向量为 {1,1,0},装入轮船的集装箱总重量为 43。
6) 结点 I 不能再扩展,成为死结点,回溯到结点 D,结点 D 已无可扩展结点,成为死结点,回溯到结点 B。
7) 结点 B 成为当前的扩展结点,沿着结点 B 向右分支结点扩展,到达结点 E,结点 E 成为活结点,并成为当前的扩展结点,第 2 个集装箱不装入轮船,此时轮船上只有第 1 个集装箱,cr=32。
8) 沿着结点 E 往左分支扩展,结点 J 成为活结点,并成为当前的扩展结点,将第 3 个集装箱装入轮船,此时有 cr=32-25=7,第 1 个和第 3 个集装箱装入轮船,解向量为 {1,0,1},装入轮船的总重量为 43。
9) 结点 J 不可扩展,成为死结点,回溯到结点 E,结点 E 成为当前的扩展结点,沿着结点 E 向右分支扩展,到达结点 K,结点 K 为活结点,即第 3 个集装箱不装入轮船,此时 cr=32,只有第 1 个集装箱装入轮船,解向量为 {1,0,0},装入轮船的总重量为 18。
按照以上方式继续在解空间树上搜索,搜索完毕后,即可得到装载问题的最优解,最优解为 {0,1,1}。
2) 解决旅行商问题
旅行商问题(Traveling Salesman Problem,TSP)又称为旅行推销员问题、货郎担问题,是数学领域的著名问题之一。一个旅行商要从 n 个城市的某一城市出发去往其他城市,每个城市经过且只经过一次,最后回到原来出发的城市。求在去往任何一个城市的所有路径中路径长度最短的一条。
为了方便描述该问题,可采用带权图表示 n 个城市之间的关系,顶点表示城市,顶点之间的权值表示城市之间的距离。例如,n=4 时的旅行商问题可用下图表示。

图 4 旅行商问题
图中的回路有 (1,2,3,4,1)、(1,2,4,3,1)、(1,3,2,4,1)、(1,4,2,3,1)、(1,3,4,2,1) 等,其中 (1,3,4,2,1) 的路径长度最短,其路径长度为 29。旅行商人所走过的可能路线其实是所有路径的排列组合,这些方案可绘制成一棵排列树,也是该问题的解空间树,如下图所示。

图 5 旅行商问题的解空间树
该树的深度为 5,两个结点之间的路径表示旅行商经过的城市。
利用回溯算法求解问题一般是先根据具体问题构造解空间树,也就是描述问题的解,然后在解空间树中从根结点出发搜索问题的解,直到遍历完整棵解空间树。
解空间树一般分为两种:子集树和排列树。当所给的问题是从 n 个元素的集合 S 中找出满足某种性质的子集时,相应的解空间树称为子集树。当所给问题是确定 n 个元素满足某种性质的排列时,相应的解空间树称为排列树。排列树通常有 n! 个叶子结点。因此,遍历排列树需要 O(n!) 的计算时间。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: