MATLAB qr()分解函数的用法
矩阵 A 的 QR 分解也叫正交三角分解,即将矩阵 A 表示成一个正交矩阵 Q 与一个上三角矩阵 R 的乘积形式。这种分解在工程技术中的应用最广泛。
在 MATLAB 中,矩阵 A 的 QR 分解函数是 qr(),它的调用格式及说明如下表所示。
【实例】对如下矩阵进行 QR 分解。
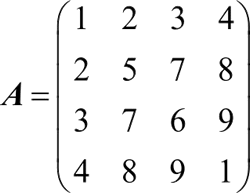
MATLAB 程序如下:
在 MATLAB 中,矩阵 A 的 QR 分解函数是 qr(),它的调用格式及说明如下表所示。
| 调用格式 | 说明 |
|---|---|
| [Q,R] = qr(A) | 返回正交矩阵 Q 和上三角矩阵 R,Q 和 R 满足 A=QR。若 A 为 mxn 矩阵,则 Q 为 mxm 矩阵,R 为 mxn 矩阵 |
| [Q,R,E] = qr(A) | 求得正交矩阵 Q 和上三角矩阵 R。E 为置换矩阵,它使得 R 的对角线元素按绝对值大小降序排 列,满足 AE=QR |
| [Q,R] = qr(A,0) | 产生矩阵 A 的“经济型”分解。若 A 为 mxn 矩阵,且 m>n,则返回 Q 的前 n 列,R 为 nxn 矩阵;否则该函数等价于 [Q,R]=qr(A) |
| [Q,R,E] = qr(A,0) | 产生矩阵 A 的“经济型”分解,E 为置换矩阵,它使得 R 的对角线元素按绝对值大小降序排列,且 A(:, E)=Q*R |
| R = qr(A) | 对稀疏矩阵 A 进行分解,只产生一个上三角矩阵 R,R 为 ATA 的 Cholesky 分解因子,即满足 RTR = ATA |
| R = qr(A,0) | 对稀疏矩阵 A 的“经济型”分解 |
| [C,R]=qr(A,b) | 此函数用来计算方程组 Ax=b 的最小二乘解 |
【实例】对如下矩阵进行 QR 分解。
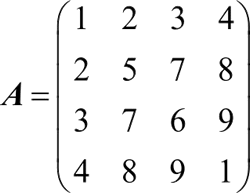
MATLAB 程序如下:
>> clear % 清除工作区的变量
>> A=[1 2 3 4;2 5 7 8;3 7 6 9;4 8 9 1]; % 创建4行4列矩阵A
>> [Q,R]=qr(A) % 对矩阵A进行QR分解,并返回正交矩阵Q和上三角矩阵R
Q =
-0.1826 0.1543 0.3322 -0.9124
-0.3651 -0.6172 0.6644 0.2106
-0.5477 -0.4629 -0.6644 -0.2106
-0.7303 0.6172 0.0830 0.2807
R =
-5.4772 -11.8673 -12.9628 -9.3113
0 -1.0801 -1.0801 -7.8695
0 0 2.4083 0.7474
0 0 0 -3.5795
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: