图的邻接矩阵表示(Java完整实现)
图的邻接矩阵(Adjacency Matrix)表示也称为数组表示。它采用两个数组来表示图:
这个关联关系数组称为邻接矩阵。对于无权图,邻接矩阵表示为:
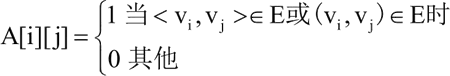
对于带权图,有:
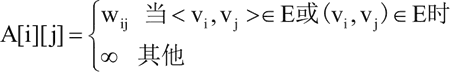
其中,wij 表示顶点 i 与顶点 j 构成的弧或边的权值,若顶点之间不存在弧或边,则用 ∞ 表示。
观察下面这两个图:
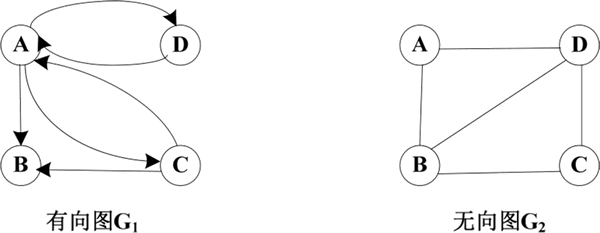
图 3 有向图G1与无向图G2
两个图的弧和边的集合分别为 A={<A,B>,<A,C>,<A,D>,<C,A>,<C,B>,<D,A>} 和 E={(A,B),(A,D),(B,C),(B,D),(C,D)}。它们的邻接矩阵表示如下图所示。
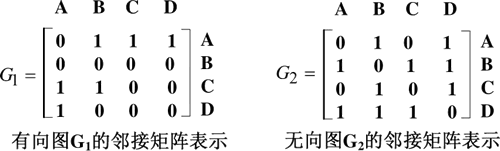
图 4 图的邻接矩阵表示
在无向图的邻接矩阵中,若存在边 (A,B),则需要将 <A,B> 和 <B,A> 的对应位置都置为 1。
带权图的邻接矩阵表示如下图所示。
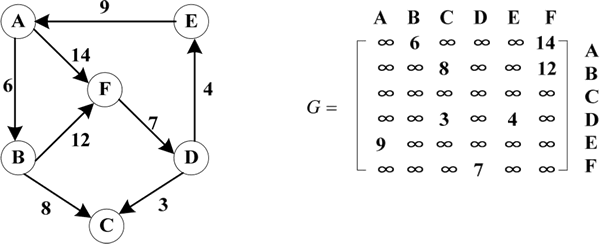
图 5 带权图的邻接矩阵表示
图的邻接矩阵存储结构描述如下:
【实例】编写算法,利用邻接矩阵表示法创建一个有向网。
- 一个是用于存储顶点信息的一维数组,
- 另一个是用于存储图中顶点之间的关联关系的二维数组。
这个关联关系数组称为邻接矩阵。对于无权图,邻接矩阵表示为:
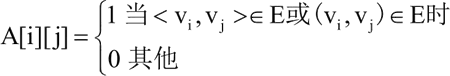
对于带权图,有:
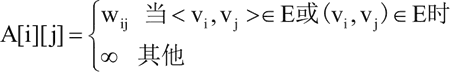
其中,wij 表示顶点 i 与顶点 j 构成的弧或边的权值,若顶点之间不存在弧或边,则用 ∞ 表示。
观察下面这两个图:

图 3 有向图G1与无向图G2
两个图的弧和边的集合分别为 A={<A,B>,<A,C>,<A,D>,<C,A>,<C,B>,<D,A>} 和 E={(A,B),(A,D),(B,C),(B,D),(C,D)}。它们的邻接矩阵表示如下图所示。

图 4 图的邻接矩阵表示
在无向图的邻接矩阵中,若存在边 (A,B),则需要将 <A,B> 和 <B,A> 的对应位置都置为 1。
带权图的邻接矩阵表示如下图所示。

图 5 带权图的邻接矩阵表示
图的邻接矩阵存储结构描述如下:
enum Kind{DG, DN, UG, UN} // 图的类型:有向图、有向网、无向图和无向网
public class MGraph
{
String vex[]; // 用于存储顶点
double arc[][]; // 邻接矩阵,存储边或弧的信息
int vexnum, arcnum; // 顶点数#边(弧)的数目
Kind kind; // 图的类型
final int MAXSIZE=20;
MGraph()
{
vex=new String[MAXSIZE];
arc=new double[MAXSIZE][MAXSIZE];
arcnum=0;
vexnum=0;
kind=Kind.UG;
}
}
其中,数组 vex 用于存储图中的顶点信息,如 A、B、C、D,数组 arc 用于存储图中顶点之间边的信息,称为邻接矩阵。【实例】编写算法,利用邻接矩阵表示法创建一个有向网。
enum Kind{DG, DN, UG, UN} // 图的类型:有向图、有向网、无向图和无向网
public class MGraph
{
String vex[]; // 用于存储顶点
double arc[][]; // 邻接矩阵,存储边或弧的信息
int vexnum, arcnum; // 顶点数#边(弧)的数目
Kind kind; // 图的类型
final int MAXSIZE=20;
MGraph()
{
vex=new String[MAXSIZE];
arc=new double[MAXSIZE][MAXSIZE];
arcnum=0;
vexnum=0;
kind=Kind.UG;
}
public void CreateGraph(Kind kind) // 采用邻接矩阵表示法创建有向网
{
System.out.println("请输入有向网 N 的顶点数,弧数:");
Scanner sc=new Scanner(System.in);
String num[]=sc.nextLine().split(" ");
vexnum=Integer.parseInt(num[0]);
arcnum=Integer.parseInt(num[1]);
System.out.println("请输入"+vexnum+"个顶点的值(字符),以空格分隔各个字符:");
String v[]=sc.nextLine().split(" ");
int i=0,j;
for(String e:v) {
vex[i++]= e;
}
for(i=0;i<vexnum;i++) // 初始化邻接矩阵
for(j=0;j<vexnum;j++)
arc[i][j]=Double.POSITIVE_INFINITY;
System.out.println("请输入"+arcnum+"条弧的弧尾 弧头 权值 (以空格作为间隔):");
System.out.println("顶点 1 顶点 2 权值:");
for(int k=0;k<arcnum;k++)
{
v=sc.nextLine().split(" "); // 输入两个顶点和弧的权值
i=LocateVertex(v[0]);
j=LocateVertex(v[1]);
arc[i][j]=Double.parseDouble(v[2]);
}
}
public int LocateVertex(String v)
// 在顶点向量中查找顶点 v, 若找到,则返回在向量中的序号, 否则返回-1
{
for(int i=0;i<vexnum;i++)
{
if(vex[i].equals(v))
return i;
}
return -1;
}
public void DisplayGraph()
// 输出邻接矩阵存储表示的图
{
System.out.print("有向网具有" + vexnum + "个顶点" + arcnum + "条弧, 顶点依次是:");
for (int i = 0; i < vexnum; i++)
System.out.print(vex[i] + " ");
System.out.println("\n有向网 N 的:");
System.out.println("序号 i");
for (int i = 0; i < vexnum; i++)
System.out.print(" "+i);
System.out.println();
for (int i = 0; i < vexnum; i++) {
System.out.print(i + " ");
for (int j = 0; j < vexnum; j++) {
if (arc[i][j] != Double.POSITIVE_INFINITY)
System.out.print(DoubleTrans(arc[i][j]) + " ");
else
System.out.print("∞" + " ");
}
System.out.println();
}
}
public String DoubleTrans(double d)
{
if(Math.round(d-d==0))
return String.valueOf((long)d);
return String.valueOf(d);
}
public void CreateGraph2(Kind kind)
// 采用邻接矩阵表示法创建有向网
{
System.out.println("请输入有向网 N 的顶点数,弧数:");
Scanner sc=new Scanner(System.in);
String num[]=sc.nextLine().split(" ");
vexnum=Integer.parseInt(num[0]);
arcnum=Integer.parseInt(num[1]);
System.out.println("请输入"+vexnum+"个顶点的值(字符),以空格分隔各个字符:");
String v[]=sc.nextLine().split(" ");
int i=0,j;
for(String e:v) {
vex[i++]= e;
}
for(i=0;i<vexnum;i++) // 初始化邻接矩阵
for(j=0;j<vexnum;j++)
arc[i][j]=Double.POSITIVE_INFINITY;
System.out.println("请输入"+arcnum+"条弧的弧尾 弧头 权值 (以空格作为间隔):");
System.out.println("顶点 1 顶点 2 权值:");
for(int k=0;k<arcnum;k++)
{
v=sc.nextLine().split(" "); // 输入两个顶点和弧的权值
i=LocateVertex(v[0]);
j=LocateVertex(v[1]);
arc[i][j]=Double.parseDouble(v[2]);
}
}
public void CreateGraph(double value[][],int vnum,int arcnum, String ch[])
{ // 采用邻接矩阵表示法创建有向网
this.vexnum=vnum;
this.arcnum=arcnum;
arc=new double[vnum][vnum];
int k=0;
for(String e: ch) {
vex[k++]=e;
}
for(int i=0;i<vexnum;i++) // 初始化邻接矩阵
for(int j=0;j<vexnum;j++)
arc[i][j] =Double.POSITIVE_INFINITY;
for(int r=0;r<value.length;r++) {
int i = (int)value[r][0];
int j = (int)value[r][1];
arc[i][j] = value[r][2];
}
}
public static void main(String args[])
{
System.out.println("创建一个有向网 N:");
MGraph N = new MGraph();
N.CreateGraph(Kind.DN);
System.out.println("输出网的顶点和弧:");
N.DisplayGraph();
}
}
程序运行结果为:
创建一个有向网 N:
请输入有向网 N 的顶点数,弧数:
5 6
请输入 5 个顶点的值(字符),以空格分隔各个字符:
A B C D E
请输入 6 条弧的弧尾 弧头 权值 (以空格作为间隔):
顶点 1 顶点 2 权值:
A B 6
A D 9
A E 14
B E 12
D C 4
E C 7
输出网的顶点和弧:
有向网具有 5 个顶点 6 条弧,顶点依次是:A B C D E
有向网 N 的:
序号 i=
0 1 2 3 4
0 ∞ 6 ∞ 9 14
1 ∞ ∞ ∞ ∞ 12
2 ∞ ∞ ∞ ∞ ∞
3 ∞ ∞ 4 ∞ ∞
4 ∞ ∞ 7 ∞ ∞
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: