贝叶斯算法详解(附带Python实例)
贝叶斯算法与大多数机器学习算法不同,如决策树、逻辑回归、支持向量机等算法,这些算法都是判别方法,可通过一个决策函数 y=f(x) 或者条件分布 p(y|x) 直接学习出特征输出 y 和特征 x 之间的关系。而贝叶斯算法的生成方法为:找出特征输出 y 和特征 x 的联合分布 p(x, y),然后用如下公式得出:
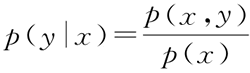
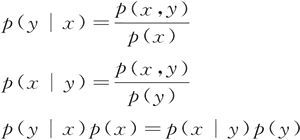
最后得到贝叶斯公式为:
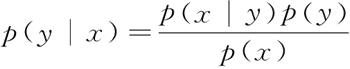
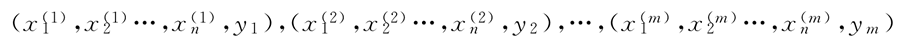
每一个样本特征 x 有 n 个体征,标签 y 有 k 个类别,定义为 c1,c2,…,ck。从已有的样本中很容易得到先验概率分布 p(y=ck)(k=1,2,…,m)。
而条件概率分布为:
然后就可以用贝叶斯公式得到 x、y 的联合分布 P(x, y),联合分布 p(x, y) 定义为:
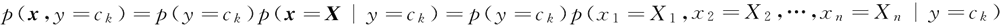
从上面可以看出 p(y=ck) 很容易得到,统计一下各类被占的比例(频数)即可求出。但是 p(x1=X1,x2=X2,…,xn=Xn|y=ck) 很难求出,因为这是一个很复杂的有 n 个维度的条件分布,因此朴素贝叶斯算法在这里做了一个大胆的假设:x 的 n 个维度之间相互独立(也就是特征之间条件独立),则可得到:
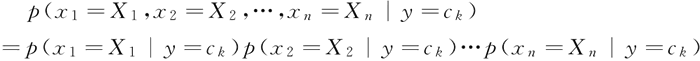
这大大简化了 n 维条件概率分布的难度,下图给出了贝叶斯算法的整体模型:
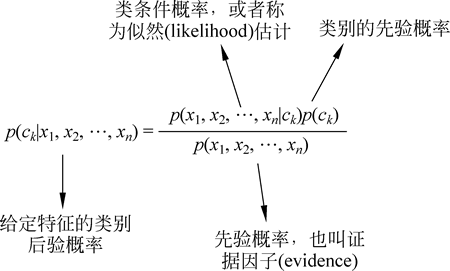
图 1 贝叶斯算法的整体模型
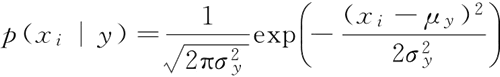
参数均值和方差都使用最大似然估计。
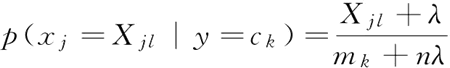
MultinomialNB 参数比 GaussianNB 多,一共有 3 个参数:
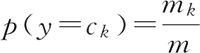
其中,m 为训练集样本总数量,mk 为输出第 k 类别的训练集样本数。
伯努利朴素贝叶斯的决策规则基于:
BernoulliNB 与多项式朴素贝叶斯的规则不同,伯努利朴素贝叶斯明确地惩罚类 y 中没有出现作为预测因子的特征 i,而多项式朴素贝叶斯只是简单地忽略没出现的特征。
【实例】使用 Iris 数据集做的一个使用正态朴素贝叶斯分类。
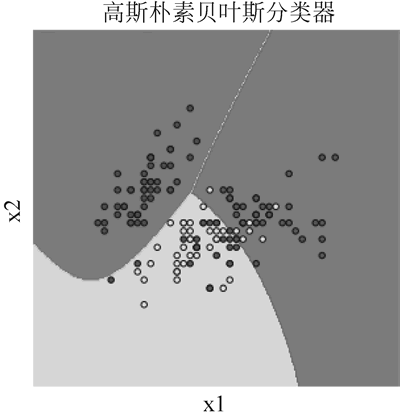
图 2 高斯朴素贝叶斯分类效果
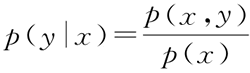
贝叶斯算法的基本思想
朴素贝叶斯算法假设自变量特征之间条件独立,可以概括为:先验概率+数据=后验概率。1) 条件独立
如果 x、y 互相独立,则有:p(x, y)=p(x)×p(y)
2) 条件概率
条件概率为: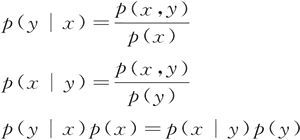
最后得到贝叶斯公式为:
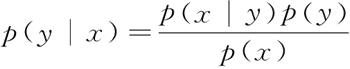
贝叶斯算法的模型
假设有 m 个样本数据: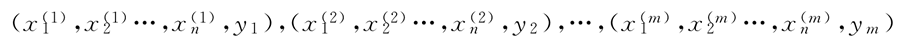
每一个样本特征 x 有 n 个体征,标签 y 有 k 个类别,定义为 c1,c2,…,ck。从已有的样本中很容易得到先验概率分布 p(y=ck)(k=1,2,…,m)。
而条件概率分布为:
p(x=X|y=ck)=p(x1=X1, x2=X2, xn=Xn|y=ck)
然后就可以用贝叶斯公式得到 x、y 的联合分布 P(x, y),联合分布 p(x, y) 定义为:
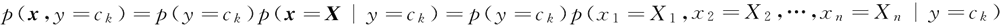
从上面可以看出 p(y=ck) 很容易得到,统计一下各类被占的比例(频数)即可求出。但是 p(x1=X1,x2=X2,…,xn=Xn|y=ck) 很难求出,因为这是一个很复杂的有 n 个维度的条件分布,因此朴素贝叶斯算法在这里做了一个大胆的假设:x 的 n 个维度之间相互独立(也就是特征之间条件独立),则可得到:
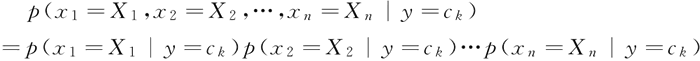
这大大简化了 n 维条件概率分布的难度,下图给出了贝叶斯算法的整体模型:

图 1 贝叶斯算法的整体模型
用sklearn实现贝叶斯分类
sklearn 提供了 3 个朴素贝叶斯的分类器,分别为:- naive_bayes.GaussianNB:高斯分布下的朴素贝叶斯。
- naive_bayes.MultinomialNB:多项式分布下的朴素贝叶斯。
- naive_bayes.BernoulliNB:伯努利分布下的朴素贝叶斯。
1) 高斯朴素贝叶斯
GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。概率假设为高斯分布: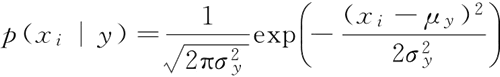
参数均值和方差都使用最大似然估计。
2) 多项式朴素贝叶斯
MultinomialNB 假设特征的先验概率为多项式分布: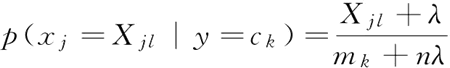
MultinomialNB 参数比 GaussianNB 多,一共有 3 个参数:
- 参数 alpha 即为公式中的常数 λ,默认值为 1。如果发现拟合得不好,需要调优时,可以选择稍大于 1 或者稍小于 1 的数;
- 参数 fit_prior 表示是否要考虑先验概率,如果是 false,则所有的样本类别输出都有相同的类别先验概率;
- 可以用第 3 个参数 class_prior 输入先验概率,或者不输入第 3 个参数 class_prior 让 MultinomialNB 自己从训练集样本来计算先验概率,此时的先验概率为:
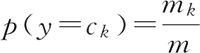
其中,m 为训练集样本总数量,mk 为输出第 k 类别的训练集样本数。
3) 伯努利朴素贝叶斯
BernoulliNB 应用于多重伯努利分布数据的朴素贝叶斯训练和分类算法,指有多个特征,但每个特征都假设是一个二元(Bernoulli,boolean)变量。因此,这类算法要求样本以二元值特征向量表示;如果样本含有其他类型的数据,一个 BernoulliNB 实例会将其二值化(取决于binarize参数)。伯努利朴素贝叶斯的决策规则基于:
p(xi|y) = p(i|y)xi+(1-p(i|y))(1-xi)
BernoulliNB 与多项式朴素贝叶斯的规则不同,伯努利朴素贝叶斯明确地惩罚类 y 中没有出现作为预测因子的特征 i,而多项式朴素贝叶斯只是简单地忽略没出现的特征。
【实例】使用 Iris 数据集做的一个使用正态朴素贝叶斯分类。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
import matplotlib
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文
#生成所有测试样本点
def make_meshgrid(x, y, h=.02):
x_min, x_max=x.min()-1, x.max()+1
y_min, y_max=y.min()-1, y.max()+1
xx, yy=np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
return xx, yy
#对测试样本进行预测, 并显示
def plot_test_results(ax, clf, xx, yy, * * params):
Z=clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z=Z.reshape(xx.shape)
#画等高线
ax.contourf(xx, yy, Z, * * params)
#载入Iris数据集
iris=datasets.load_iris()
#只使用前面两个特征
X= iris.data[:, :2]
#样本标签值
y= iris.target
#创建并训练正态朴素贝叶斯分类器
clf=GaussianNB()
clf.fit(X, y)
title=('高斯朴素贝叶斯分类器')
fig, ax=plt.subplots(figsize=(5, 5))
plt.subplots_adjust(wspace=0.4, hspace=0.4)
#分别取出两个特征
X0, X1=X[:, 0], X[:, 1]
#生成所有测试样本点
xx, yy=make_meshgrid(X0, X1)
#显示测试样本的分类结果
plot_test_results(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
#显示训练样本
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_xticks())
ax.set_yticks())
ax.set_title(title)
plt.show()
运行程序,效果如下图所示:
图 2 高斯朴素贝叶斯分类效果
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: