朴素贝叶斯分类器(非常详细,附带实例)
在机器学习中,贝叶斯分类器是一种简单的概率分类器,它基于应用贝叶斯定理。
朴素贝叶斯分类器使用的特征模型做出了很强的独立性假设。这意味着一个类的特定特征的存在与其他所有特征的存在是独立的或无关的。
贝叶斯公式可以看作是一种条件概率公式的推广:
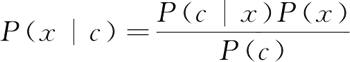
为了避开这个困难,朴素贝叶斯分类器采用了“属性条件独立性假设”:已知类别,假设所有属性相互独立。换言之,假设每个属性独立地分类结果发生影响。
基于属性条件独立性假设,上式可重写为:
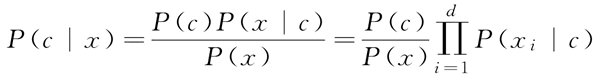
其中,d 为属性数目,xi 为 x 在第 i 个属性上的取值。
由于对所有类别来说 P(x) 相同,因此基于贝叶斯判定准则,有:
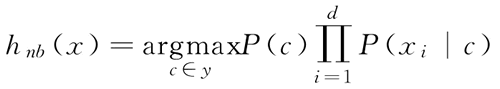
这就是朴素贝叶斯分类器的表达式。
显然,朴素贝叶斯分类器的训练过程就是基于训练集 D 来估计类先验概率 P(c),并为每个属性估计条件概率 P(xi|c)。
令 Dc 表示训练集 D 中第 c 类样本组成的集合,如果有充足的独立同分布样本,则可容易地估计出类先验概率:
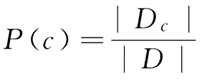
对离散属性而言,令 Dc,Xi 表示 Dc 中在第 i 个属性上取值为 xi 的样本组成的集合,则条件概率 P(xi|c) 可估计为:
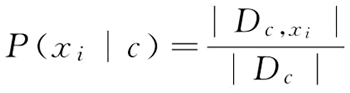
对连续属性可考虑概率密度函数,假定:
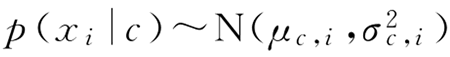
其中 μc,i 和 σc2,i 分别是第 c 类样本在第 i 个属性上取值的均值和方差,则有:
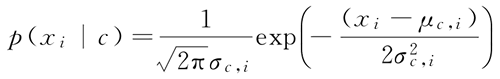
同样地,用 0 代表否,1 代表是,可以得到另外一个数组:
同时,在 y 为 1 时,也就是在下雨的 3 天当中,有 1 天刮北风,3 天全部都比较闷热,且 3 天全部出现了多云的现象,但这 3 天的天气预报都没有预报有雨。
那么对朴素贝叶斯来说,它会根据上述的计算进行推理。它会认为,如果某一天天气预报没有播有雨,但出现了多云的情况,它会倾向于把这一天放到“下雨”这一个分类中。
下面利用 Python 进行验证:
那么如果有另外一天,刮了北风,而且很闷热,但云量不多,同时天气预报说有雨,又会怎样呢?通过代码验证:
下面利用 predict_proba 方法实现朴素贝叶斯预测准确率:
再尝试第二天的预测情况:
朴素贝叶斯分类器使用的特征模型做出了很强的独立性假设。这意味着一个类的特定特征的存在与其他所有特征的存在是独立的或无关的。
贝叶斯分类器
贝叶斯分类器的分类原理:根据某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类。- 先验概率:指根据以往经验和分析得到的概率,即通过我们已经得到的训练集得到的概率;
- 后验概率:需要求得、预测的概率,并且通过这种概率去估计样本的可能类别。
贝叶斯公式可以看作是一种条件概率公式的推广:
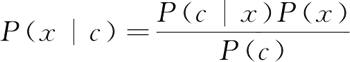
朴素贝叶斯分类定理
不难发现,基于贝叶斯公式估计后验概率 P(c|x) 的主要困难在于,类条件概率 P(x|c) 是所有属性上的联合概率,难以从有限的训练样本直接估计而得。为了避开这个困难,朴素贝叶斯分类器采用了“属性条件独立性假设”:已知类别,假设所有属性相互独立。换言之,假设每个属性独立地分类结果发生影响。
基于属性条件独立性假设,上式可重写为:
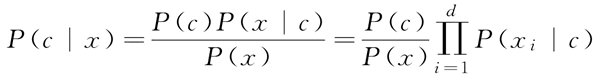
其中,d 为属性数目,xi 为 x 在第 i 个属性上的取值。
由于对所有类别来说 P(x) 相同,因此基于贝叶斯判定准则,有:
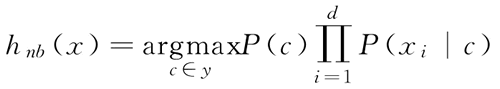
这就是朴素贝叶斯分类器的表达式。
显然,朴素贝叶斯分类器的训练过程就是基于训练集 D 来估计类先验概率 P(c),并为每个属性估计条件概率 P(xi|c)。
令 Dc 表示训练集 D 中第 c 类样本组成的集合,如果有充足的独立同分布样本,则可容易地估计出类先验概率:
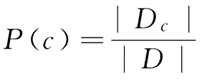
对离散属性而言,令 Dc,Xi 表示 Dc 中在第 i 个属性上取值为 xi 的样本组成的集合,则条件概率 P(xi|c) 可估计为:
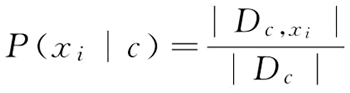
对连续属性可考虑概率密度函数,假定:
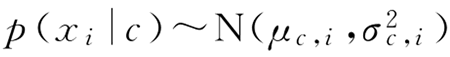
其中 μc,i 和 σc2,i 分别是第 c 类样本在第 i 个属性上取值的均值和方差,则有:
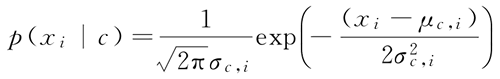
朴素贝叶斯的简单应用
过去的 7 天当中,有 3 天下雨,4 天没有下雨。用 0 代表没有下雨,1 代表下雨,则可以用一个数组来表示:y=[0,1,1,0,1,0,0]而在这 7 天当中,还有另外一些与气象有关的信息,包括是否刮北风、闷热、多云,以及天气预报给出的是否有雨信息,如下表所示。
| 刮北风 | 闷热 | 多云 | 天气预报有雨 | |
|---|---|---|---|---|
| 第 1 天 | 否 | 是 | 否 | 是 |
| 第 2 天 | 是 | 是 | 是 | 否 |
| 第 3 天 | 否 | 是 | 是 | 否 |
| 第 4 天 | 否 | 否 | 否 | 是 |
| 第 5 天 | 否 | 是 | 是 | 否 |
| 第 6 天 | 否 | 是 | 否 | 是 |
| 第 7 天 | 是 | 否 | 否 | 是 |
同样地,用 0 代表否,1 代表是,可以得到另外一个数组:
X=[0,1,0,1],[1,1,1,0],[0,1,1,0],[0,0,0,1][0,1,1,0],[0,1,0,1],[1,0,0,1]实现的 Python 代码为:
import numpy as np
#将X,y赋值为np数组
X = np.array([[0,1,0,1],
[1,1,1,0],
[0,1,1,0],
[0,0,0,1],
[0,1,1,0],
[0,1,0,1],
[1,0,0,1]])
y = np.array([0,1,1,0,1,0,0])
#对不同分类计算每个特征为1的数量
counts = {}
for label in np.unique(y):
counts[label] = X[y = = label].sum(axis = 0)
print("feature counts:\n{}".format(counts))
运行结果为:
feature counts:
{0:array([1,2,0,4]),1:array([1,3,3,0])}
同时,在 y 为 1 时,也就是在下雨的 3 天当中,有 1 天刮北风,3 天全部都比较闷热,且 3 天全部出现了多云的现象,但这 3 天的天气预报都没有预报有雨。
那么对朴素贝叶斯来说,它会根据上述的计算进行推理。它会认为,如果某一天天气预报没有播有雨,但出现了多云的情况,它会倾向于把这一天放到“下雨”这一个分类中。
下面利用 Python 进行验证:
from sklearn.naive_bayes import BernoulliNB
clf = BernoulliNB()
clf.fit(X,y)
#要进行预测的这一天,没有刮北风,也不闷热
#但是多云,天气预报没有说有雨
Next_Day = [[0,0,1,0]]
pre = clf.predict(Next_Day)
if pre = = [1]:
print("要下雨啦!")
else:
print("又是一个艳阳天!")
运行结果为:
要下雨啦!
由结果可看出,朴素贝叶斯分类器把这一天放到会下雨的分类当中。那么如果有另外一天,刮了北风,而且很闷热,但云量不多,同时天气预报说有雨,又会怎样呢?通过代码验证:
Another_day = [[1,1,0,1]]
pre2 = clf.predict(Another_day)
if pre2 = = [1]:
print("要下雨啦!")
else:
print("又是一个艳阳天!")
运行结果为:
又是一个艳阳天!这次分类器把这一天归为不会下雨的分类中了。
下面利用 predict_proba 方法实现朴素贝叶斯预测准确率:
clf.predict_proba(Next_Day)运行结果为:
array([[0.13848881, 0.86151119]])
由结果可看出,所预测的第一天,不下雨的概率约是 13.8%,而下雨的概率约是 86.2%。再尝试第二天的预测情况:
clf.predict_proba(Another_day)运行结果为:
array([[0.92340878, 0.07659122]])
由结果可看出,第二天不下雨的概率约是 92.3%,下雨的概率只有约 7.7%。从结果可看出,朴素贝叶斯做出的预测还是可以的。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: