贝叶斯分类器详解(Python实现)
贝叶斯分类器是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器。它的设计方法是一种最基本的统计分类方法。
贝叶斯分类器的分类原理是通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类。
1) 行动空间 A,它是某项实际工作中可能采取的各种“行动”所构成的集合。
注意,贝叶斯学派注意的是模型参数,所以通常而言我们想要做出的“行动”是“决策模型的参数”。因此我们通常会将行动空间取为参数空间,亦即 A=θ。
2) 决策 δx̃ 是样本空间 X 到行动空间 A 的一个映射。换句话说,对于一个单一的样本 x̃(x̃ ∈ x),决策函数可以利用它得到 A 中的一个行动。
注意,这里的样本 x̃ 通常是高维的随机向量:
3) 损失函数 L(θ, a) = LL(θ, δ(x̃)),它表示参数 θ(θ∈Θ,Θ 是参数空间)时采取行动 a(a∈A)所引起的损失。
4) 决策风险 R(θ, δ),它是损失函数的期望:
5) 先验分布:描述了参数 θ 在已知样本中的分布。
6) 平均风险 ρ(δ),它定义为决策风险 R(θ, δ) 在先验分布下的期望:
7) 贝叶斯决策 δ*,它满足:
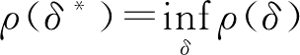
换句话说,贝叶斯决策 δ* 是在某个先验分布下使得平均风险最小的决策。
寻找一般意义下的贝叶斯决策是相当不易的数学问题,为简洁起见,需要结合具体的算法来推导相应的贝叶斯决策。
“风险”(误判损失)=原本为 cj 的样本误分类成 ci 产生的期望损失(如下式,概率乘以损失为期望损失):

为了最小化总体风险,只需在每个样本上选择能够使条件风险 R(c|X) 最小的类别标记:
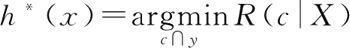
h* 称为贝叶斯最优分类器,与之对应的总体风险为贝叶斯风险,令 λ 等于 1 时,最优贝叶斯分类器是使后验概率 P(c|X) 最大。
利用贝叶斯判定准则来最小化决策风险,首先要获得后验概率 P(c|X),机器学习则是基于有限的训练样本集尽可能准确地估计出后验概率 P(c|X)。通常有两种模型:
P(c) 是类“先验”概述,P(X|c) 是样本 X 相对于类标记条件概率,或称似然。对同一个似然函数,如果存在一个参数值,使得它的函数值达到最大,那么这个值就是最为“合理”的参数值。
对于 P(c) 而言,它代表样本空间中各类样本所占的比例,根据大数定理当训练集包含充足的独立同分布样本时,可通过各类样本出现的频率进行估计。对于 P(X|c) 而言,涉及关于所有属性的联合概率,无法根据样本出现的频率进行估计。
下面通过一个实例来演示贝叶斯分类器对给定数据进行分类。
【实例】利用贝叶斯分类器对下表中的水果进行分类。
根据需要,建立一个 bayes_classfier.py 文件,实现叶斯分类器源码:
建立一个 generate_attries.py 函数,实现产生测试数据集来测试贝叶斯分类器的预测能力:
建立一个 classification.py 函数,实现使用贝叶斯分类器对测试结果进行分类:
贝叶斯分类器的分类原理是通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类。
贝叶斯分类相关知识
在学习贝叶斯分类前,我们先来了解几个与贝叶斯分类相关的概率论和数理统计的定义和知识。1) 行动空间 A,它是某项实际工作中可能采取的各种“行动”所构成的集合。
注意,贝叶斯学派注意的是模型参数,所以通常而言我们想要做出的“行动”是“决策模型的参数”。因此我们通常会将行动空间取为参数空间,亦即 A=θ。
2) 决策 δx̃ 是样本空间 X 到行动空间 A 的一个映射。换句话说,对于一个单一的样本 x̃(x̃ ∈ x),决策函数可以利用它得到 A 中的一个行动。
注意,这里的样本 x̃ 通常是高维的随机向量:
x̃ = (x1, x2,..., xN)T尤其需要分清的是,这个 x̃ 其实是一般意义上的“训练集”,xi 才是一般意义上的“样本”。
3) 损失函数 L(θ, a) = LL(θ, δ(x̃)),它表示参数 θ(θ∈Θ,Θ 是参数空间)时采取行动 a(a∈A)所引起的损失。
4) 决策风险 R(θ, δ),它是损失函数的期望:
R(θ, δ) = EL(θ, δ(x̃))
5) 先验分布:描述了参数 θ 在已知样本中的分布。
6) 平均风险 ρ(δ),它定义为决策风险 R(θ, δ) 在先验分布下的期望:
ρ(δ) = EξR(θ, δ)
7) 贝叶斯决策 δ*,它满足:
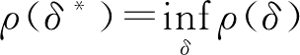
换句话说,贝叶斯决策 δ* 是在某个先验分布下使得平均风险最小的决策。
寻找一般意义下的贝叶斯决策是相当不易的数学问题,为简洁起见,需要结合具体的算法来推导相应的贝叶斯决策。
贝叶斯原理
贝叶斯决策论在相关概率已知的情况下利用误判损失来选择最优的类别分类。“风险”(误判损失)=原本为 cj 的样本误分类成 ci 产生的期望损失(如下式,概率乘以损失为期望损失):

为了最小化总体风险,只需在每个样本上选择能够使条件风险 R(c|X) 最小的类别标记:
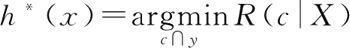
h* 称为贝叶斯最优分类器,与之对应的总体风险为贝叶斯风险,令 λ 等于 1 时,最优贝叶斯分类器是使后验概率 P(c|X) 最大。
利用贝叶斯判定准则来最小化决策风险,首先要获得后验概率 P(c|X),机器学习则是基于有限的训练样本集尽可能准确地估计出后验概率 P(c|X)。通常有两种模型:
- “判别式模型”:通过直接建模 P(c|X) 来预测(决策树,BP 神经网络,支持向量机);
- “生成式模型”:通过对联合概率模型 P(X, c) 进行建模,然后再获得 P(c|X)。
P(c) 是类“先验”概述,P(X|c) 是样本 X 相对于类标记条件概率,或称似然。对同一个似然函数,如果存在一个参数值,使得它的函数值达到最大,那么这个值就是最为“合理”的参数值。
对于 P(c) 而言,它代表样本空间中各类样本所占的比例,根据大数定理当训练集包含充足的独立同分布样本时,可通过各类样本出现的频率进行估计。对于 P(X|c) 而言,涉及关于所有属性的联合概率,无法根据样本出现的频率进行估计。
贝叶斯分类的实现
在机器学习领域,贝叶斯分类器是基于贝叶斯理论并假设各特征相互独立的分类方法,其基本方法为:使用特征向量来表征某个实体,并在该实体上绑定一个标签来代表其所属的类别。下面通过一个实例来演示贝叶斯分类器对给定数据进行分类。
【实例】利用贝叶斯分类器对下表中的水果进行分类。
| 类别 | 较长 | 不长 | 甜 | 不甜 | 黄色 | 不是黄色 | 总数 |
|---|---|---|---|---|---|---|---|
| 香蕉 | 400 | 100 | 350 | 150 | 450 | 50 | 500 |
| 橘子 | 0 | 300 | 150 | 150 | 300 | 0 | 300 |
| 其他水果 | 100 | 100 | 150 | 50 | 50 | 150 | 200 |
| 总数 | 500 | 500 | 650 | 350 | 800 | 200 | 1000 |
根据需要,建立一个 bayes_classfier.py 文件,实现叶斯分类器源码:
"""
贝叶斯分类器
"""
### 训练数据集
datasets = {'banana':{'long':400,'not_long':100,'sweet':350,'not_sweet':150,
'yellow':450,'not_yellow':50}, 'orange':{'long':0,'not_long':300,
'sweet':150,'not_sweet':150,'yellow':300,'not_yellow':0}, 'other_fruit':
{'long':100,'not_long':100,'sweet':150,'not_sweet':50,'yellow':50,
'not_yellow':150}}
def count_total(data):
'''计算各种水果的总数
return {'banana':500 ...}'''
count = {}
total = 0
for fruit in data:
'''因为水果要么甜要么不甜,可以用这两种特征来统计总数'''
count[fruit] = data[fruit]['sweet'] + data[fruit]['not_sweet']
total += count[fruit]
return count, total
def cal_base_rates(data):
'''计算各种水果的先验概率
return {'banana':0.5 ...}'''
categories, total = count_total(data)
cal_base_rates = {}
for label in categories:
priori_prob = categories[label]/total
cal_base_rates[label] = priori_prob
return cal_base_rates
def likelihood_prob(data):
'''计算各个特征值在已知水果下的概率
{'banana':{'long':0.8 ...}'''
count, _ = count_total(data)
likelihood = {}
for fruit in data:
'''创建一个临时字典,存储各个特征值的概率'''
attr_prob = {}
for attr in data[fruit]:
#计算各个特征值在已知水果下的概率
attr_prob[attr] = data[fruit][attr]/count[fruit]
likelihood[fruit] = attr_prob
return likelihood
def evidence_prob(data):
'''计算特征的概率对分类结果的影响
return {'long':50% ...}'''
#水果的所有特征
attrs = list(data['banana'].keys())
count, total = count_total(data)
evidence_prob = {}
#计算各种特征的概率
for attr in attrs:
attr_total = 0
for fruit in data:
attr_total += data[fruit][attr]
evidence_prob[attr] = attr_total/total
return evidence_prob
#以上是训练数据用到的函数,即将数据转换为代码计算概率
class naive_bayes_classifier:
'''初始化贝叶斯分类器,实例化时会调用__init__函数'''
def __init__(self, data=datasets):
self._data = datasets
self._labels = {key for key in self._data.keys()}
self._priori_prob = cal_base_rates(self._data)
self._likelihood_prob = likelihood_prob(self._data)
self._evidence_prob = evidence_prob(self._data)
#下面的函数可以直接调用上面类中定义的变量
def get_label(self, length, sweetness,color):
'''获取某一组特征值的类别'''
self._attrs = [length,sweetness,color]
res = {}
for label in self._labels:
prob = self._priori_prob[label]#取某水果占比率
for attr in self._attrs:
#单个水果的某个特征概率除以总的某个特征概率,再乘以某水果占比率
prob*=self._likelihood_prob[label][attr]/self._evidence_prob[attr]
res[label] = prob
return res
建立一个 generate_attries.py 函数,实现产生测试数据集来测试贝叶斯分类器的预测能力:
import random
def random_attr(pair):
#生成 0-1 之间的随机数
return pair[random.randint(0,1)]
def gen_attrs():
#特征值的取值集合
sets = [('long','not_long'),('sweet','not_sweet'),('yellow','not_yellow')]
test_datasets = []
for i in range(20):
#使用 map 函数生成一组特征值
test_datasets.append(list(map(random_attr,sets)))
return test_datasets
print(gen_attrs())
建立一个 classification.py 函数,实现使用贝叶斯分类器对测试结果进行分类:
import operator
import bayes_classifier
import generate_attries
def main():
test_datasets = generate_attries.gen_attrs()
classifier = bayes_classifier.naive_bayes_classifier()
for data in test_datasets:
print("特征值:",end='\t')
print(data)
print("预测结果:", end='\t')
res=classifier.get_label(*data)#表示多参传入
print(res)#预测属于哪种水果的概率
print('水果类别:',end='\t')
#对后验概率排序,输出概率最大的标签
print(sorted(res.items(),key=operator.itemgetter(1),reverse=True)[0][0])
if __name__ == '__main__':
#表示模块既可以被导入(到 Python shell 或者其他模块中),也可以作为脚本来执行。
#当模块被导入时,模块名称是文件名;当模块作为脚本独立运行时,名称为 __main__。
main()
运行程序,输出如下:
预测结果: {'banana': 0.1076923076923077, 'orange': 0.0, 'other_fruit': 0.8653846153846153}
水果类别: other_fruit
特征值: ['long', 'not_sweet', 'yellow']
预测结果: {'banana': 0.7714285714285716, 'orange': 0.0, 'other_fruit': 0.04464285714285715}
水果类别: banana
...
特征值: ['long', 'not_sweet', 'yellow']
预测结果: {'banana': 0.7714285714285716, 'orange': 0.0, 'other_fruit': 0.04464285714285715}
水果类别: banana
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: