MATLAB interp1()插值函数的用法(附带实例)
插值法是一种古老的数学方法。插值问题的数学定义如下:
1) 先由实验或测量的方法得到函数 y=f(x) 在互异点 x0,x1,…,xn处的数值y0,y1,…,yn,见下图:

图 1 一维插值示意图
2) 然后构造一个函数 ϕ(x) 作为 y=f(x) 的近似表达式,即:
插值的任务是由已知的观测点为物理量建立一个简单、连续的解析模型,以便能根据该模型推测该物理量在非观测点处的特性。
插值包括多项式插值、埃尔米特插值、分段插值与样条插值、三角函数插值、辛克插值等。插值在数据分析、信号处理、图像处理等诸多领域有着十分重要的应用。
当被插值函数 y=f(x) 为一元函数时,为一维插值。MATLAB 使用 interp1() 函数来实现一维插值。
interp1() 函数的调用格式如下:
上述几种插值方法的比较如下:
要选择一种插值方法,需要考虑的因素包括运算时间、占用计算机内存的大小和插值的平滑性。
【实例】利用 interp1() 函数对 y=sinx 进行分段线性插值。在编辑器窗口中编写如下代码:
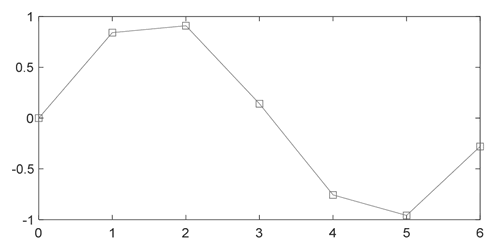
图 2 分段线性插值结果
1) 先由实验或测量的方法得到函数 y=f(x) 在互异点 x0,x1,…,xn处的数值y0,y1,…,yn,见下图:

图 1 一维插值示意图
2) 然后构造一个函数 ϕ(x) 作为 y=f(x) 的近似表达式,即:
y=f(x)≈ϕ(x)使得 ϕ(x0)=y0,ϕ(x1)=y1,…,ϕ(xn)=yn。这类问题称为插值问题,y=f(x) 称为被插值函数,ϕ(x) 称为插值函数,x0,x1,…,xn 称为插值节点。
插值的任务是由已知的观测点为物理量建立一个简单、连续的解析模型,以便能根据该模型推测该物理量在非观测点处的特性。
插值包括多项式插值、埃尔米特插值、分段插值与样条插值、三角函数插值、辛克插值等。插值在数据分析、信号处理、图像处理等诸多领域有着十分重要的应用。
当被插值函数 y=f(x) 为一元函数时,为一维插值。MATLAB 使用 interp1() 函数来实现一维插值。
interp1() 函数的调用格式如下:
vq=interp1(x,v,xq) vq=interp1(x,v,xq,method)
- x 为自变量的取值范围;
- v 为函数值,或者为一个向量,其长度必须与 x 保持一致;
- xq 为插值点向量或数组;
-
method 是字符串变量,用来设定插值方法,常用的插值方法如下:
- 'nearest':邻近点插值,插值点函数值估计为与该插值点最近的数据点的函数值。
- 'linear':线性插值,根据相邻数据点的线性函数估计落在该区域内插值数据点的函数值。
- 'spline':三次样条插值。这种方法在相邻数据点间建立三次多项式函数,根据多项式函数确定插值数据点的函数值。
- 'pchip'或'cubic':立方插值,通过分段立方埃尔米特插值方法计算插值结果。
- 'v5cubic':MATLAB 5 版本中的三次样条插值。
上述几种插值方法的比较如下:
- 邻近点插值方法的速度最快,但平滑性最差。
- 线性插值方法占用的计算机内存比邻近点插值方法的大,运算时间也长;与邻近点插值方法不同的是,其结果是连续的,但顶点处的斜率会改变。
- 三次样条插值方法的运算时间最长,但内存的占用较立方插值方法的小,其插值数据和导数都是连续的。在这几种插值方法中,三次样条插值结果的平滑性最好,但如果输入数据不一致或数据点过近,就可能出现平滑性很差的插值效果。
要选择一种插值方法,需要考虑的因素包括运算时间、占用计算机内存的大小和插值的平滑性。
【实例】利用 interp1() 函数对 y=sinx 进行分段线性插值。在编辑器窗口中编写如下代码:
clear all; x = 0:2*pi; y = sin(x); xx = 0:0.5:2*pi; yy = interp1(x, y, xx); plot(x, y, 's', xx, yy)运行结果如下图所示:

图 2 分段线性插值结果
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: