MATLAB dsolve()函数:求解微分方程(附带实例)
微分方程是数学的重要分支之一,大致与微积分同时产生,并随实际需要而发展。在高等数学中,将含自变量、未知函数和它的微商(或偏微商)的方程称为常(或偏)微分方程,如:
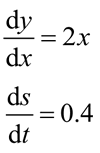
一般地,未知函数是一元函数的,叫作常微分方程;未知函数是多元函数的,叫作偏微分方程。微分方程有时也简称方程。
在 MATLAB 中,实现微分方程求解的函数是 dsolve(),它的调用格式及说明如下表所示:
【实例 1】求解微分方程,MATLAB 程序如下:
【实例 2】求微分方程 y′2+5y′−xy=0 的通解,MATLAB 程序如下:
【实例 3】求微分方程 xy′−5y′+x3=0 在 y(1)=0、y(5)=0 时的解,并绘制解的曲线。MATLAB 程序如下:
1) 求方程的解:
2) 绘制曲线:

图 2 微分方程的解
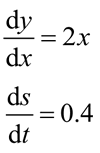
一般地,未知函数是一元函数的,叫作常微分方程;未知函数是多元函数的,叫作偏微分方程。微分方程有时也简称方程。
在 MATLAB 中,实现微分方程求解的函数是 dsolve(),它的调用格式及说明如下表所示:
| 调用格式 | 说明 |
|---|---|
| S = dsolve(eqn) | 求解常微分方程,eqn 是一个使用 diff 和 “=” 表示微分方程的符号方程 |
| S = dsolve(eqn,cond) | 用初始条件或边界条件求解常微分方程 |
| S = dsolve(eqn,cond,Name,Value) | 使用一个或多个名称-值对组参数指定附加选项 |
| Y = dsolve(eqns) | 求解常微分方程组,并返回包含解的结构数组。结构数组中的字段数量对应系统中独立变量的数量 |
| Y = dsolve(eqns,conds) | 用初始条件或边界条件 conds 求解常微分方程组 eqns |
| Y = dsolve(eqns,conds,Name,Value) | 使用一个或多个名称-值对组参数指定附加选项 |
| [y1,…,yN] = dsolve(eqns) | 求解常微分方程组,并将解分配给变量 |
| [y1,…,yN] = dsolve(eqns,conds) | 用初始条件或边界条件 conds 求解常微分方程组 eqns |
| [y1,…,yN] = dsolve(eqns,conds,Name,Value) | 使用一个或多个名称-值对组参数指定附加选项 |
【实例 1】求解微分方程,MATLAB 程序如下:
>> close all % 关闭当前已打开的文件
>> clear % 清除工作区的变量
>> syms x(t) y(t) % 定义符号函数x(t)和y(t)
>> eqns=[diff(x,t)==y,diff(y,t)==-x]; % 输入微分方程组
>> S=dsolve(eqns) % 求解微分方程组
S =
包含以下字段的 struct:
y: [1x1 sym]
x: [1x1 sym]
>> disp(' ') % 显示空值
>> disp(['微分方程组的解',blanks(2),'x',blanks(22),'y'])%显示指定的内容
微分方程的解 x y
>> disp([S.x,S.y]) % 显示方程的解
[ C1*cos(t) + C2*sin(t), C2*cos(t) - C1*sin(t)]
【实例 2】求微分方程 y′2+5y′−xy=0 的通解,MATLAB 程序如下:
>> clear all % 清除工作区的变量
>> syms y(x) % 定义符号函数y(x)
>> eqn=diff(y,x,2)+5*diff(y,x)-x*y==0; % 定义符号表达式
>> y=dsolve(eqn) % 求解微分方程
y =
(C1*airy(0, x + 25/4))/exp(5*x)^(1/2) + (C2*airy(2, x + 25/4))/exp(5*x)^(1/2)
【实例 3】求微分方程 xy′−5y′+x3=0 在 y(1)=0、y(5)=0 时的解,并绘制解的曲线。MATLAB 程序如下:
1) 求方程的解:
>> close all % 关闭当前已打开的文件 >> clear % 清除工作区的变量 >> syms y(x) % 定义符号函数y(x) >> eqn=x*diff(y,x,2)-5*diff(y,x)+x^3==0; % 定义符号表达式 >> y=dsolve(eqn,'y(1)=0,y(5)=0','x') % 求解微分方程 y = - (13*x^6)/2604 + x^4/8 - 625/5208
2) 绘制曲线:
>> xn=-1:6; % 创建介于-1~6的向量,默认间隔值为1 >> yn=subs(y,'x',xn) % 将表达式y中的所有x替换为xn yn = [ 0, -625/5208, 0, 387/248, 592/93, 2835/248, 0, -1705/24] >> fplot(y,[-1 6]) % 在指定区间绘制表达式的图像 >> axis([-1 6 -10 15]) % 调整坐标轴的范围 >> hold on % 保留当前坐标区的绘图 >> plot([1,5],[0,0],'.r','MarkerSize',20) % 使用大小为20的、红色的点标记绘制指定位置的图像 >> text(1,1,'y(1)=0') % 在指定位置为数据点添加文本说明 >> text(4,1,'y(5)=0') >> title(['x*D2y - 5*Dy = -x^3',', y(1)=0,y(5)=0']) % 为图像添加标题 >> hold off % 关闭保持命令绘图结果如下图所示:

图 2 微分方程的解
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: