MATLAB quiver3()函数的用法(附带实例)
MATLAB 中绘制三维图形箭头图的函数是 quiver3(),其与二维图形箭头图的绘制函数 quiver() 的调用格式及说明十分相似,只是多一个坐标参数。
下面介绍 quiver3() 函数的调用格式及说明,如下表所示。
【实例 1】绘制下述公式的火柴杆图、法线方向向量和箭头图:
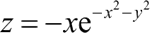
MATLAB 程序如下:
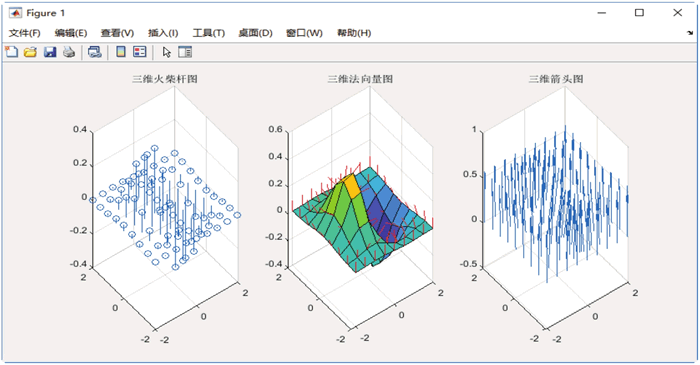
图 2 绘图结果
【实例 2】绘制 Z=−XcosY 上的三维箭头图。在 MATLAB 命令行窗口中输入如下命令:
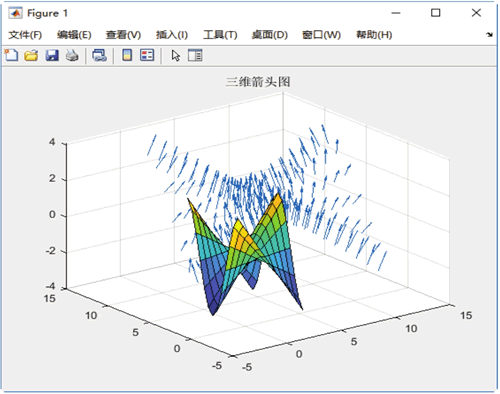
图 3 三维箭头图
下面介绍 quiver3() 函数的调用格式及说明,如下表所示。
| 调用格式 | 说明 |
|---|---|
| quiver3(x,y,z,u,v,w) | 在确定的点处绘制向量,其方向由分量 (u,v,w) 确定。矩阵 x、y、z、u、v 和 w 必须具有相同大小并包含对应的位置和向量分量 |
| quiver3(z,u,v,w) | 在沿曲面 z 的等间距点处绘制向量,其方向由分量 (u,v,w) 确定 |
| Quiver3(...,scale) | 自动对向量的长度进行处理,使之不会重叠,可以对 scale 进行取值。若 scale=2,则向量长度伸长 2 倍;若 scale=0,则如实画出向量图 |
| Quiver3(...,LineSpec) | 用 LineSpec 指定的线型、符号、颜色等画向量图 |
| Quiver3(...,LineSpec,'filled') | 对用 LineSpec 指定的记号进行填充 |
| Quiver3(...,'PropertyName',PropertyValue,...) | 为该函数创建的箭头图对象指定属性名称和属性值对组 |
| quiver3(ax,...) | 将图形绘制到 ax 指定的坐标区中,而不是当前坐标区(gca)中 |
| h = quiver3(...) | 返回每个向量图的句柄 |
【实例 1】绘制下述公式的火柴杆图、法线方向向量和箭头图:
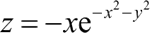
MATLAB 程序如下:
>> close all % 关闭当前已打开的文件
>> clear % 清除工作区的变量
>> [X,Y]=meshgrid(-2:0.5:2); % 通过向量定义网格数据X、Y
>> Z=-X.*exp(-X.^2-Y.^2); % 通过网格数据X、Y定义函数表达式 Z
>> [U,V,W]= surfnorm(X,Y,Z); % 定义三维曲面法向量
>> subplot(1,3,1),stem3(X,Y,Z),title('三维火柴杆图') % 绘制三维火柴杆图
>> subplot(1,3,2),surfnorm (X,Y,Z),title('三维法向量图') % 绘制三维法向量图
>> subplot(1,3,3),quiver3(X,Y,Z,U,V,W),title('三维箭头图') % 绘制三维箭头图
运行结果如下图所示:
图 2 绘图结果
【实例 2】绘制 Z=−XcosY 上的三维箭头图。在 MATLAB 命令行窗口中输入如下命令:
>> close all % 关闭当前已打开的文件
>> clear % 清除工作区的变量
>> x = -3:0.5:3; % 创建-3~3的向量x,元素间隔为0.5
>> y = x; % 将向量x赋值给向量y
>> [X,Y] = meshgrid(x,y); % 通过向量x、y定义网格数据X、Y
>> Z = -X.*cos(Y); % 通过网格数据X、Y定义函数表达式 Z
>> surf(X,Y,Z) % 根据网格数据创建三维曲面
>> hold on % 打开图形保持函数
>> [U,V,W] = surfnorm(Z); % 绘制矩阵 Z 的曲面,输出三维曲面法向量U,V,W
>> quiver3(Z,U,V,W) % 绘制三维箭头图
>> title('三维箭头图') % 添加标题
>> hold off % 关闭图形保持函数
运行结果如下图所示:
图 3 三维箭头图
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: