MATLAB diff()求导函数的用法(附带实例)
符号微分运算实际上就是计算函数的导(函)数,MATLAB 提供的 diff() 函数不仅可求函数的一阶导数,还可以计算函数的高阶导数与偏导数。
diff() 函数的调用格式如下:
注意,函数 f 为矩阵时,是对元素逐个进行求导的,且自变量定义在整个矩阵上。
【实例】已知下面的函数:
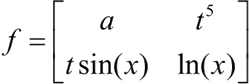
试求下面表达式的值:
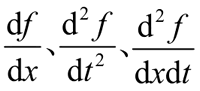
在命令行窗口中输入以下语句,并查看输出结果:
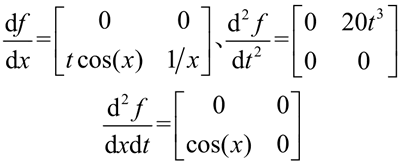
diff() 函数的调用格式如下:
Df=diff(f) % 求符号表达式 f 的 1 阶导数,求导变量由 symvar(f,1)确定
Df=diff(f,n) % 计算 f 的第 n 阶导数,求导变量由 symvar 确定
Df=diff(f,var) % 对 f 关于变量 var 进行求导
% var 可以是符号变量(如 x)、符号函数(如 f(x)),或导数函数(如 diff(f(t),t))
Df=diff(f,var,n) % 计算 f 关于变量 var 的第 n 阶导数
Df=diff(f,var1,...,varN) % 对 f 分别关于多个变量 var1,...,varN 进行求导
Df=diff(f,mvar) % 对符号矩阵表达式 f 关于变量 mvar 进行求导
求函数高阶导数很容易通过输入参数 n 的值来实现;对于求多元函数的偏导数,除指定的自变量外的其他变量均当作常数处理。注意,函数 f 为矩阵时,是对元素逐个进行求导的,且自变量定义在整个矩阵上。
【实例】已知下面的函数:
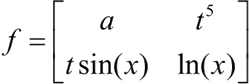
试求下面表达式的值:
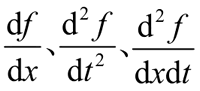
在命令行窗口中输入以下语句,并查看输出结果:
>> syms a t x
>> f=[a t^5; t*sin(x) log(x)];
>> df=diff(f)
df =
[ 0, 0, 0]
[t*cos(x), 1/x]
>> dfdt2=diff(f,t,2)
dfdt2 =
[0, 20*t^3]
[0, 0]
>> dfdxdtt=diff(diff(f,x),t)
dfdxdtt =
[ 0,0]
[cos(x),0]
即: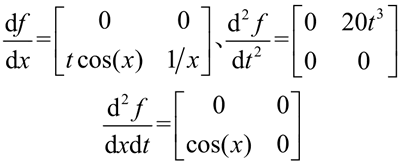
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: