二进制、八进制和十六进制详解(附带示意图)
在编程过程中,我们除了会使用十进制来表示数字,还会使用二进制、八进制和十六进制,它们在某些情况下比十进制更加直观。
我们平时使用的数字都是由 0~9 共十个数字组成的,例如 1、9、20、472、7023 等,一个数字最多能表示九,如果要表示十、十一、二十九、一百等,就需要多个数字组合起来。
例如表示 6+7 的结果,一个数字不够,只能“进位”,用 13 来表示;这时“进一位”相当于十,“进两位”相当于二十。
因为逢十进一(满十进一),也因为只有 0~9 共十个数字,所以叫做十进制(Decimalism)。十进制是在人类社会发展过程中自然形成的,它符合人们的思维习惯,例如人类有十根手指和脚趾。
进制也就是进位制。进行加法运算时逢 n 进一(满 n 进一),进行减法运算时借一当 n,这就是 n 进制,这种进制也就包含 n 个数字,基数为 n。十进制有 0~9 共10个数字,基数为10,在加减法运算中,逢十进一,借一当十。
在计算机内部,数据都是以二进制的形式存储的,二进制是学习编程必须掌握的基础。
二进制加减法和十进制加减法的思想是类似的:
下面两张示意图详细演示了二进制加减法的运算过程。
1) 二进制加法:1+0=1、1+1=10、11+10=101、111+111=1110
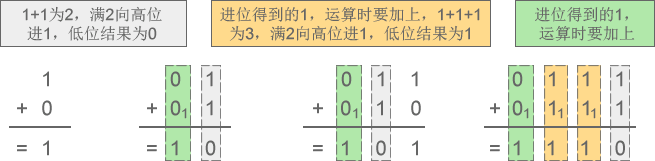
图1:二进制加法示意图
2) 二进制减法:1-0=1、10-1=1、101-11=10、1100-111=101

图2:二进制减法示意图
八进制有 0~7 共 8 个数字,基数为 8,加法运算时逢八进一,减法运算时借一当八。例如,数字 0、1、5、7、14、733、67001、25430 都是有效的八进制。
下面两张图详细演示了八进制加减法的运算过程。
1) 八进制加法:3+4=7、5+6=13、75+42=137、2427+567=3216
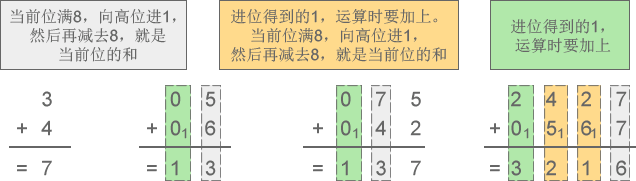
图3:八进制加法示意图
2) 八进制减法:6-4=2、52-27=23、307-141=146、7430-1451=5757
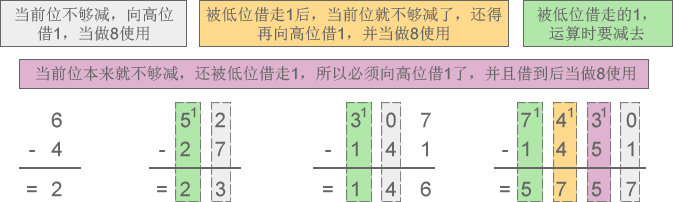
图4:八进制减法示意图
十六进制中,用 A 来表示 10,B 表示 11,C 表示 12,D 表示 13,E 表示 14,F 表示 15,因此有 0~F 共 16 个数字,基数为 16,加法运算时逢 16 进 1,减法运算时借 1 当 16。例如,数字 0、1、6、9、A、D、F、419、EA32、80A3、BC00 都是有效的十六进制。
1) 十六进制加法:6+7=D、18+BA=D2、595+792=D27、2F87+F8A=3F11
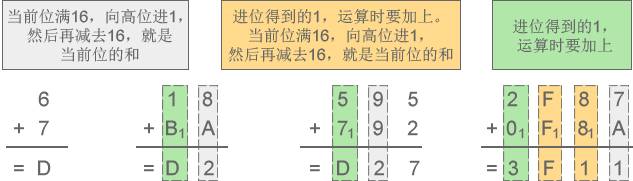
图5:十六进制加法示意图
2) 十六进制减法:D-3=A、52-2F=23、E07-141=CC6、7CA0-1CB1=5FEF
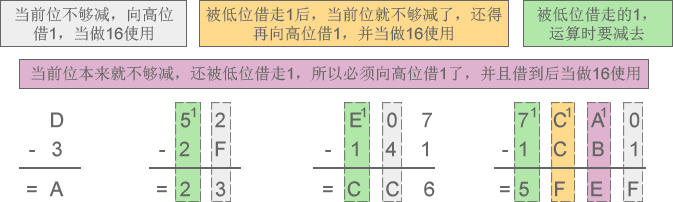
图6:十六进制减法示意图
我们平时使用的数字都是由 0~9 共十个数字组成的,例如 1、9、20、472、7023 等,一个数字最多能表示九,如果要表示十、十一、二十九、一百等,就需要多个数字组合起来。
例如表示 6+7 的结果,一个数字不够,只能“进位”,用 13 来表示;这时“进一位”相当于十,“进两位”相当于二十。
因为逢十进一(满十进一),也因为只有 0~9 共十个数字,所以叫做十进制(Decimalism)。十进制是在人类社会发展过程中自然形成的,它符合人们的思维习惯,例如人类有十根手指和脚趾。
进制也就是进位制。进行加法运算时逢 n 进一(满 n 进一),进行减法运算时借一当 n,这就是 n 进制,这种进制也就包含 n 个数字,基数为 n。十进制有 0~9 共10个数字,基数为10,在加减法运算中,逢十进一,借一当十。
二进制
我们不妨将思维拓展一下,既然可以用 0~9 共十个数字来表示数值,那么也可以用 0、1 两个数字来表示数值,这就是二进制(Binary)。例如,数字 0、1、10、111、100、1000001 都是有效的二进制。在计算机内部,数据都是以二进制的形式存储的,二进制是学习编程必须掌握的基础。
二进制加减法和十进制加减法的思想是类似的:
- 对于十进制,进行加法运算时逢十进一,进行减法运算时借一当十;
- 对于二进制,进行加法运算时逢二进一,进行减法运算时借一当二。
下面两张示意图详细演示了二进制加减法的运算过程。
1) 二进制加法:1+0=1、1+1=10、11+10=101、111+111=1110

图1:二进制加法示意图
2) 二进制减法:1-0=1、10-1=1、101-11=10、1100-111=101

图2:二进制减法示意图
八进制
除了二进制,编程中常用的还有八进制和十六进制;本文先介绍八进制,稍后再介绍十六进制。八进制有 0~7 共 8 个数字,基数为 8,加法运算时逢八进一,减法运算时借一当八。例如,数字 0、1、5、7、14、733、67001、25430 都是有效的八进制。
下面两张图详细演示了八进制加减法的运算过程。
1) 八进制加法:3+4=7、5+6=13、75+42=137、2427+567=3216

图3:八进制加法示意图
2) 八进制减法:6-4=2、52-27=23、307-141=146、7430-1451=5757

图4:八进制减法示意图
十六进制
除了二进制和八进制,十六进制也经常使用,甚至比八进制还要频繁。十六进制中,用 A 来表示 10,B 表示 11,C 表示 12,D 表示 13,E 表示 14,F 表示 15,因此有 0~F 共 16 个数字,基数为 16,加法运算时逢 16 进 1,减法运算时借 1 当 16。例如,数字 0、1、6、9、A、D、F、419、EA32、80A3、BC00 都是有效的十六进制。
注意,十六进制中的字母不区分大小写,ABCDEF 也可以写作 abcdef。下面两张图详细演示了十六进制加减法的运算过程。
1) 十六进制加法:6+7=D、18+BA=D2、595+792=D27、2F87+F8A=3F11

图5:十六进制加法示意图
2) 十六进制减法:D-3=A、52-2F=23、E07-141=CC6、7CA0-1CB1=5FEF

图6:十六进制减法示意图
总结
计算机的底层硬件都是二进制的(《数据在内存中的存储形式》一文中有介绍),而八进制、十六进制和二进制之间的转换更加简单和直观,所以在某些特殊场景中会使用八进制和十六进制,而不使用十进制。
举几个例子:
- Unix/Linux 操作系统中表示文件权限使用八进制,比如 777 表示最大权限,能够读取、写入和执行。
- 内存地址经常用十六进制来表示,比如 2A5DF72B。
- 在 Web 前端开发中,通常使用十六进制来表示颜色,比如 #FF0000 表示纯红色,#C52CC3 表示一种紫色。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: