时间复杂度和空间复杂度(附带实例,新手必看)
瑞士著名科学家 N.Wirth 提出:数据结构+算法=程序。数据结构是程序的骨架,算法是程序的灵魂。
算法是对特定问题解决步骤的一种体现方式,不依赖任何语言,既可以用自然语言、C、C++、Java、Python 等体现,也可以用流程图、框图体现。对于同一个问题,可以采用不同的算法解决。那么,怎样才算一个好算法呢?
先看一个例子,写一个算法,求序列之和:-1,1,-1,1,…,(-1)^n。看到这个例子时,你会怎么想?是用 for 语句,还是用 while 语句?
先看算法 sum1:
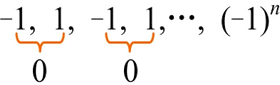
再看算法 sum2:
假设 n=10^8,运行两个程序,比较运行结果和运行时间:
再看一个例子,假设第 1 个月有一对刚诞生的兔子,第 2 个月兔子进入成熟期,第 3 个月兔子开始生育兔子,而一对成熟的兔子每月都会生育一对兔子,兔子永不死去……那么,从一对初生兔子开始,12 个月后会有多少对兔子呢?n 个月后又会有多少对兔子呢?
兔子数列即斐波那契数列,这个数列有一个十分明显的特点:从第 3 个月开始,当月兔子数=上月兔子数+当月新生兔子数,而当月新生兔子数正好是上上月兔子数,因此,前面相邻两项之和构成了后一项,即当月兔子数=上月兔子数+上上月兔子数。斐波那契数列为 1,1,2,3,5,8,13,21,34…
斐波那契数列表达式如下:
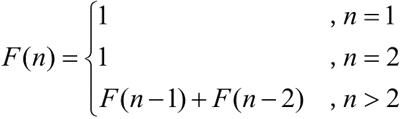
将斐波那契数列表达式直接写成递归程序:
若采用数组存储每一项,则从前向后递推,可以写成非递归程序:
两个程序的运行结果和运行时间如下:
不知你是否发现,第 2 个程序在 n=10 时,time2=3;在 n=30 时,time2=2。当数值变大时,运行时间反而变短了!其实,同一台机器,每次的运行时间都可能不同,更不必说在不同的机器上运行了。因此在计算算法的时间复杂度时,并不是真的在计算算法的运行时间。
好算法的衡量标准如下:
算法复杂度包括时间复杂度和空间复杂度。除前 3 条基本标准外,好算法的评判标准就是高效和低存储,高效即时间复杂度低,低存储即空间复杂度低。
举个简单的例子:
算法运行时间主要取决于最高项,后面的可以忽略不计。因为若你告诉朋友买车花了 20 万零 199 元,则朋友会认为你花了 20 万元,并不关心尾数。若一个人是亿万富翁,则不管其是有 2 亿元还是有 10 亿元,都是亿万富翁。因此在表达时舍小项、舍系数,只看最高项就可以了。若用时间复杂度的渐进上界 O 表示,则该算法的时间复杂度为
其实完全没有必要计算每行代码的运行次数,只计算出现频率最多的语句的运行次数即可。循环内层的语句往往是运行次数最多的,对运行时间贡献最大。
例如,在下面的算法中,“total=total+i*j”是对时间复杂度贡献最大的语句,只计算该语句的运行次数即可。该算法的时间复杂度为 O(n^2)。
并不是对每个算法都能直接计算运行次数。对于某些算法如排序、查找、插入等,可以按最好、最坏和平均情况分别求其渐进复杂度。但在考查一个算法时,通常考查最坏情况,而不是考查最好情况,因为最坏情况对于衡量算法的好坏具有实际意义。
输入和输出数据占用的内存空间是必需的。算法本身占用的内存空间可以通过精简算法来压缩,但压缩的量很小,可以忽略不计。程序在运行时使用的辅助变量占用的内存空间就是辅助空间,是衡量空间复杂度的关键因素。一般将算法的辅助空间作为衡量空间复杂度的标准。
例如,将两个数交换:
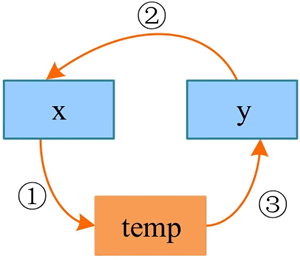
上图中的步骤标号与函数 swap() 中的语句标号一一对应,该算法使用了一个辅助空间 temp,空间复杂度为
注意 在递归算法中,每次递推都需要一个栈空间来保存调用记彔,因此在计算空间复杂度时需要计算递归栈的辅助空间。
例如,计算 n 的阶乘:
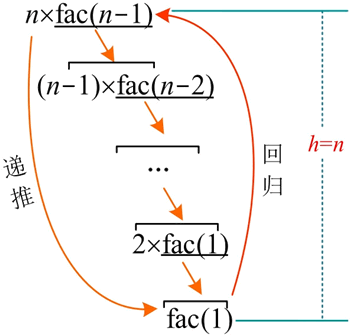
计算 n 的阶乘时,递归树的深度为 n,因此计算 n 的阶乘的递归算法的空间复杂度为 O(n)。
常见算法的时间复杂度如下:
常见的时间复杂度函数曲线如下图所示:
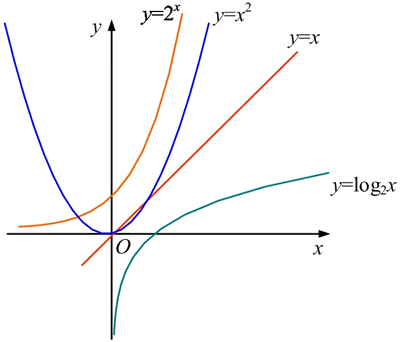
从上图可以看出,指数阶增量随着 x 的增加而急剧增加,而对数阶增量增加缓慢。它们之间的关系为:
算法是对特定问题解决步骤的一种体现方式,不依赖任何语言,既可以用自然语言、C、C++、Java、Python 等体现,也可以用流程图、框图体现。对于同一个问题,可以采用不同的算法解决。那么,怎样才算一个好算法呢?
先看一个例子,写一个算法,求序列之和:-1,1,-1,1,…,(-1)^n。看到这个例子时,你会怎么想?是用 for 语句,还是用 while 语句?
先看算法 sum1:
int sum1(int n) {
int sum = 0;
for(int i = 1; i <= n; i++)
sum += pow(-1, i); // 表示 (-1)^i
return sum;
}
该算法可以实现求和运算,但是为什么不这样运算?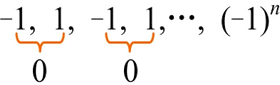
再看算法 sum2:
int sum2(int n) {
int sum = 0;
if (n % 2 == 0)
sum = 0;
else
sum = -1;
}
假设 n=10^8,运行两个程序,比较运行结果和运行时间:
sum1=0 time1=10124
sum2=0 time2=0
再看一个例子,假设第 1 个月有一对刚诞生的兔子,第 2 个月兔子进入成熟期,第 3 个月兔子开始生育兔子,而一对成熟的兔子每月都会生育一对兔子,兔子永不死去……那么,从一对初生兔子开始,12 个月后会有多少对兔子呢?n 个月后又会有多少对兔子呢?
兔子数列即斐波那契数列,这个数列有一个十分明显的特点:从第 3 个月开始,当月兔子数=上月兔子数+当月新生兔子数,而当月新生兔子数正好是上上月兔子数,因此,前面相邻两项之和构成了后一项,即当月兔子数=上月兔子数+上上月兔子数。斐波那契数列为 1,1,2,3,5,8,13,21,34…
斐波那契数列表达式如下:
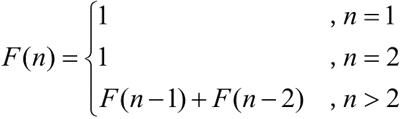
将斐波那契数列表达式直接写成递归程序:
long double fib1(int n) {
if (n < 1)
return -1;
else if (n == 1 || n == 2)
return 1;
else
return fib1(n - 1) + fib1(n - 2);
}
若采用数组存储每一项,则从前向后递推,可以写成非递归程序:
long double fib2(int n) {
if (n < 1)
return -1;
long double *a = new long double[n + 1];
a[1] = a[2] = 1;
for (int i = 3; i <= n; i++) {
a[i] = a[i - 1] + a[i - 2];
cout << a[i] << endl;
}
}
两个程序的运行结果和运行时间如下:
fib1(10)=55 time1=4 fib2(10)=55 time2=3 fib1(30)=832040 time1=17 fib2(30)=832040 time2=2 fib1(50)=1.25863e+010 time1=76269 fib2(50)=1.25863e+010 time2=6 fib1(100)=------------------------- fib2(100)=3.54225e+020 time2=151两个程序的运行结果都正确,但是运行时间随着数据规模 n 的增加,差距越来越大。第 1 个程序计算到 100 的时候,已经非常缓慢了,缓慢到让人无法忍受,以至于将运行窗口关闭。
不知你是否发现,第 2 个程序在 n=10 时,time2=3;在 n=30 时,time2=2。当数值变大时,运行时间反而变短了!其实,同一台机器,每次的运行时间都可能不同,更不必说在不同的机器上运行了。因此在计算算法的时间复杂度时,并不是真的在计算算法的运行时间。
好算法的衡量标准如下:
- 1) 正确性:指算法能够满足解决具体问题的需求,程序运行正常,无语法错误,能够通过典型的软件测试,达到预期的需求规格。
- 2) 易读性:指算法遵循标识符命名规则,简洁、易懂,注释语句恰当、适量,既便于自己和他人阅读,也便于后期调试和修改。
- 3) 健壮性:指算法对非法数据及操作有较好的反应和处理。例如,在信息管理系统中登记电话号码时,少输入 1 位,系统就应该提示出错。
- 4) 高效性:指算法运行效率高,即算法运行所消耗的时间短。算法的时间复杂度就是算法运行需要的时间。现代计算机 1 秒能计算数亿次,因此不能用秒来具体计算算法消耗的时间。由于采用相同配置的计算机进行一次基本运算的时间是一定的,所以我们可以用算法基本运算的执行次数来衡量算法效率,即将算法基本运算的执行次数作为时间复杂度的衡量标准。
- 5) 低存储性:指算法所需的内存空间少。尤其像手机、Pad 这样的嵌入式设备,若算法占用内存空间过大,则无法执行。
算法复杂度包括时间复杂度和空间复杂度。除前 3 条基本标准外,好算法的评判标准就是高效和低存储,高效即时间复杂度低,低存储即空间复杂度低。
时间复杂度
时间复杂度指算法运行需要的时间。一般将算法基本运算的执行次数作为时间复杂度的衡量标准。举个简单的例子:
int sum(int n) {
int sum = 0; // 1次
for (int i = 1; i <= n; i++) // n+1 次
sum += i; // n 次
return sum; // 1 次
}
总执行次数为 2×n+3。若用一个函数 T(n) 表达:T(n)=2n+3,则当 n 足够大时,例如 n=10^5 时,T(n)=2×10^5+3。算法运行时间主要取决于最高项,后面的可以忽略不计。因为若你告诉朋友买车花了 20 万零 199 元,则朋友会认为你花了 20 万元,并不关心尾数。若一个人是亿万富翁,则不管其是有 2 亿元还是有 10 亿元,都是亿万富翁。因此在表达时舍小项、舍系数,只看最高项就可以了。若用时间复杂度的渐进上界 O 表示,则该算法的时间复杂度为
O(n)。其实完全没有必要计算每行代码的运行次数,只计算出现频率最多的语句的运行次数即可。循环内层的语句往往是运行次数最多的,对运行时间贡献最大。
例如,在下面的算法中,“total=total+i*j”是对时间复杂度贡献最大的语句,只计算该语句的运行次数即可。该算法的时间复杂度为 O(n^2)。
并不是对每个算法都能直接计算运行次数。对于某些算法如排序、查找、插入等,可以按最好、最坏和平均情况分别求其渐进复杂度。但在考查一个算法时,通常考查最坏情况,而不是考查最好情况,因为最坏情况对于衡量算法的好坏具有实际意义。
空间复杂度
空间复杂度指算法在运行过程中占用了多少内存空间。算法占用的内存空间包括:输入和输出数据占用的内存空间、算法本身占用的内存空间、额外需要的辅助空间。输入和输出数据占用的内存空间是必需的。算法本身占用的内存空间可以通过精简算法来压缩,但压缩的量很小,可以忽略不计。程序在运行时使用的辅助变量占用的内存空间就是辅助空间,是衡量空间复杂度的关键因素。一般将算法的辅助空间作为衡量空间复杂度的标准。
例如,将两个数交换:
void swap(int x, int y) { // x 与 y 交换
int temp;
temp = x; // ① temp 为辅助空间
x = y; // ②
y = temp; // ③
}
这两个数的交换过程如下图所示:
上图中的步骤标号与函数 swap() 中的语句标号一一对应,该算法使用了一个辅助空间 temp,空间复杂度为
O(1)。注意 在递归算法中,每次递推都需要一个栈空间来保存调用记彔,因此在计算空间复杂度时需要计算递归栈的辅助空间。
例如,计算 n 的阶乘:
long long fac(int n) {
if (n < 0)
return -1;
else if (n == 0 || n == 1)
return 1;
else
return n * fac(n - 1);
}
递推和回归在系统内部使用栈实现,栈空间的大小为递归树的深度。计算 n 的阶乘,其递归树如下图所示:
计算 n 的阶乘时,递归树的深度为 n,因此计算 n 的阶乘的递归算法的空间复杂度为 O(n)。
常见算法的时间复杂度如下:
- 常数阶:算法运行的次数是一个常数,例如 5、20、100,通常用 O(1) 表示。
- 对数阶:具有对数阶时间复杂度的算法的运行效率较高,常见的有 O(logn)、O(nlogn) 等。
- 多项式阶:对很多算法的时间复杂度都可以用多项式表达,常见的有 O(n)、O(n^2)、O(n^3)等。
- 指数阶:具有指数阶时间复杂度的算法的运行效率极差,是程序员避之不及的,常见的有 O(2^n)、O(n!)、O(n^n) 等。
常见的时间复杂度函数曲线如下图所示:

从上图可以看出,指数阶增量随着 x 的增加而急剧增加,而对数阶增量增加缓慢。它们之间的关系为:
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: