算法时间复杂度和空间复杂度(Java实现)
算法分析的目的是看设计的算法是否具有可行性,并尽可能挑选运行效率较高的算法。
一般情况下,随着 n 的增大,T(n) 增长较慢的算法为最优的算法。例如,在下列 3 个程序段中,给出基本操作 x=x+1 的时间复杂度分析。
程序段 1:
程序段 2:
程序段 3:
常用的时间复杂度所耗费的时间从小到大依次是:
一些常见函数的增长率如下图所示:
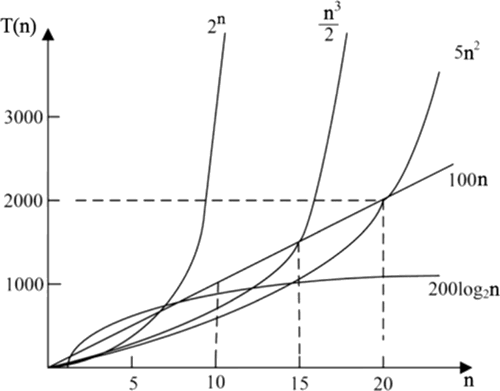
图 1 常见函数的增长率
一般情况下,算法的时间复杂度只需要考虑关于问题规模 n 的增长率或阶数。例如以下程序段:
在某些情况下,算法的基本操作的重复执行次数不仅依赖于输入数据集的规模,还依赖于数据集的初始状态。例如,在以下的冒泡排序算法中,其基本操作执行次数还取决于数据元素的初始排列状态:
对这类算法的分析,一种方法是计算所有情况的平均值,这种时间复杂度的计算方法称为平均时间复杂度;另一种方法是计算最坏情况下的时间复杂度,这种方法称为最坏时间复杂度。若数组 a 中的初始输入数据可能出现 n! 种排列情况的概率相等,则冒泡排序的平均时间复杂度为 T(n)=O(n^2)。
然而,在很多情况下,各种输入数据集出现的概率难以确定,算法的平均时间复杂度也就难以确定。因此,另一种更可行,更常用的办法是讨论算法在最坏情况下的时间复杂度,即分析最坏情况以估算算法执行时间的上界。
例如,上面的冒泡排序的最坏时间复杂度为数组 a 中的初始序列为从大到小有序,则冒泡排序算法在最坏情况下的时间复杂度为 T(n)=O(n^2)。
【实例 1】分析以下程序段的时间复杂度。
【实例 2】分析以下算法的时间复杂度。
【实例 3】分析以下算法的时间复杂度。
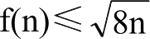
所以时间复杂度为:
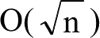
【实例 4】一个算法所需的时间由以下递归方程表示,分析算法的时间复杂度。
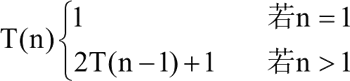
根据以上递归方程,可得:
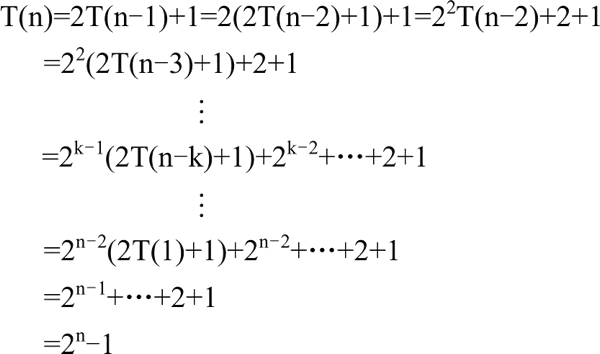
因此,该算法的时间复杂度为 O(2^n)。
一般情况下,一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元。若输入数据所占存储空间只取决于问题本身,和算法无关,则只需要分析该算法在实现时所需的辅助空间即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为 O(1)。
【实例 5】以下是一个简单的插入排序算法,分析算法的空间复杂度。
【实例 6】以下算法是求 n 个数中的最大者,分析算法的空间复杂度。
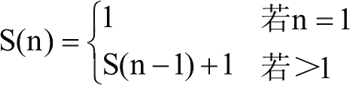
则有 S(n)=S(n-1)+1=S(n-2)+1+1=…=S(1)+1+1+…+1=O(n)。因此,该算法的空间复杂度为 O(n)。
算法的时间复杂度
在进行算法分析时,语句总的执行次数 f(n) 是关于问题规模 n 的函数,可以分析 f(n) 随 n 的变化情况并确定 f(n) 的数量级。算法的时间复杂度也就是算法的时间量度,记作:T(n)=O(f(n))
它表示随问题规模 n 的增大,算法的执行时间的增长率和 f(n) 的增长率相同,称作算法的渐进时间复杂度(Asymptotic Time Complexity),简称时间复杂度,记作 T(n)。其中,f(n) 是问题规模 n 的某个函数。一般情况下,随着 n 的增大,T(n) 增长较慢的算法为最优的算法。例如,在下列 3 个程序段中,给出基本操作 x=x+1 的时间复杂度分析。
程序段 1:
x = x + 1;
程序段 2:
for(i = 1;i < n+1;i++)
x = x + 1;
程序段 3:
for(i = 1;i < n+1;i++)
for(j = 1;j < n+1;j++)
x = x + 1;
程序段 1 的时间复杂度为 O(1),称为常量阶;程序段 2 的时间复杂度为 O(n),称为线性阶;程序段 3 的时间复杂度为 O(n^2),称为平方阶。此外,算法的时间复杂度还有对数阶 O(log2n)、指数阶 O(2^n)等。常用的时间复杂度所耗费的时间从小到大依次是:
O(1) < O(log2n) < O(n) < O(n^2) < O(n^3) < O(2^n) < O(n!)算法的时间复杂度是衡量一个算法好坏的重要指标。一般情况下,具有指数级的时间复杂度的算法只有当 n 足够小时才是可使用的算法。具有常量阶、线性阶、对数阶、平方阶和立方阶的时间复杂度的算法是常用的算法。
一些常见函数的增长率如下图所示:

图 1 常见函数的增长率
一般情况下,算法的时间复杂度只需要考虑关于问题规模 n 的增长率或阶数。例如以下程序段:
for(i = 1;i < n + 1;i++)
for(j = 2;j < i;j++)
{
k++;
a[i][j] = k;
}
语句 k++ 的执行次数关于 n 的增长率为 n^2,它是语句频度 (n-1)(n-2)/2 中增长最快的项。在某些情况下,算法的基本操作的重复执行次数不仅依赖于输入数据集的规模,还依赖于数据集的初始状态。例如,在以下的冒泡排序算法中,其基本操作执行次数还取决于数据元素的初始排列状态:
void Bubble(int a[], int n)
{
boolean change = true;
for (int i = 1; i < n; i++) {
if (change) {
change = false;
for (int j = 1; j < n - i + 1; j++) {
if (a[j] > a[j + 1]) {
int t = a[j];
a[j] = a[j + 1];
a[j + 1] = t;
change = true;
}
}
}
}
}
交换相邻的两个整数为该算法中的基本操作:
- 当数组 a 中的初始序列为从小到大排序的有序排列时,其基本操作的执行次数为 0;
- 当数组中的初始序列从大到小排列时,其基本操作的执行次数为 n(n-1)/2。
对这类算法的分析,一种方法是计算所有情况的平均值,这种时间复杂度的计算方法称为平均时间复杂度;另一种方法是计算最坏情况下的时间复杂度,这种方法称为最坏时间复杂度。若数组 a 中的初始输入数据可能出现 n! 种排列情况的概率相等,则冒泡排序的平均时间复杂度为 T(n)=O(n^2)。
然而,在很多情况下,各种输入数据集出现的概率难以确定,算法的平均时间复杂度也就难以确定。因此,另一种更可行,更常用的办法是讨论算法在最坏情况下的时间复杂度,即分析最坏情况以估算算法执行时间的上界。
例如,上面的冒泡排序的最坏时间复杂度为数组 a 中的初始序列为从大到小有序,则冒泡排序算法在最坏情况下的时间复杂度为 T(n)=O(n^2)。
算法的时间复杂度分析举例
一般情况下,算法的时间复杂度只需要考虑算法中的基本操作,即算法中最深层语句的操作。【实例 1】分析以下程序段的时间复杂度。
for(i = 1;i < n;i++)
for(j = 2;j < i;j++)
{
x = x + 1;
a[i][j] = x;
}
该程序段中的基本操作是内层 for 循环中的语句,即 x=x+1 和 a[i][j]=x,其语句频度为 (n-1)(n-2)/2。因此,其时间复杂度为 O(n^2)。【实例 2】分析以下算法的时间复杂度。
void Fun(){
int i = 1;
while(i <= n)
i = i * 2;
}
函数 Fun() 的基本运算是 i=i*2,设执行次数为 f(n),2f(n)≤n,则有 f(n)≤log2n。因此,时间复杂度为 O(log2n)。【实例 3】分析以下算法的时间复杂度。
void Fun(){
int i = 0;
int s = 0;
while(s <= n)
{
i = i + 1;
s += i;
}
}
该算法中的基本操作是 while 循环中的语句,设 while 循环次数为 f(n),则变量 i 从 0 到 f(n),循环次数为 f(n)*(f(n)+1)/2≤n,计算 f(n) 最终得到: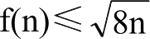
所以时间复杂度为:
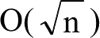
【实例 4】一个算法所需的时间由以下递归方程表示,分析算法的时间复杂度。
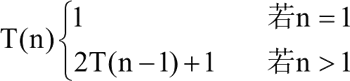
根据以上递归方程,可得:
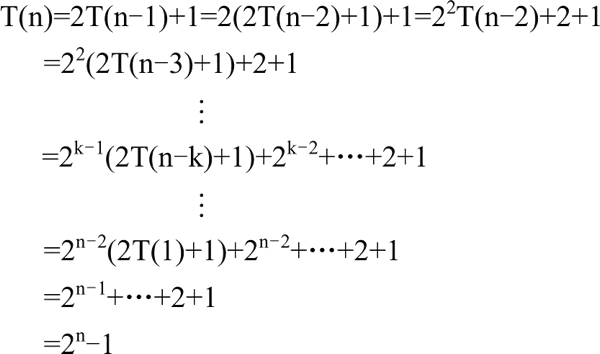
因此,该算法的时间复杂度为 O(2^n)。
算法的空间复杂度
空间复杂度(Space Complexity)作为算法所需存储空间的量度,记作:S(n)=O(f(n))
其中,n 为问题的规模,f(n) 为语句关于 n 所占存储空间的函数。一般情况下,一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元。若输入数据所占存储空间只取决于问题本身,和算法无关,则只需要分析该算法在实现时所需的辅助空间即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为 O(1)。
【实例 5】以下是一个简单的插入排序算法,分析算法的空间复杂度。
for (i = 0; i < n - 1; i++) {
t = a[i + 1];
j = i;
while (j >= 0 && t < a[j]) {
a[j + 1] = a[j];
j = j - 1;
}
a[j + 1] = t;
}
该算法借助了变量 t,与问题规模 n 的大小无关,空间复杂度为 O(1)。【实例 6】以下算法是求 n 个数中的最大者,分析算法的空间复杂度。
int FindMax(int a[], int n)
{
if (n <= 1)
return a[0];
else {
int m = FindMax(a, n - 1);
return a[n - 1] >= m ? a[n - 1] : m;
}
}
设 FindMax(a,n) 占用的临时空间为 S(n),由以上算法可得到以下占用临时空间的递推式。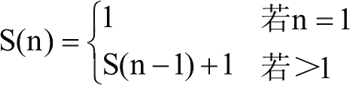
则有 S(n)=S(n-1)+1=S(n-2)+1+1=…=S(1)+1+1+…+1=O(n)。因此,该算法的空间复杂度为 O(n)。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: