二分查找算法(图文并茂,Python实现)
二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好,占用系统内存较少;其缺点是要求待查表为有序表,且插入删除困难。
因此,折半查找方法适用于不经常变动而查找频繁的有序列表。
当序列不能被定位时,则查找失败,并结束查找过程。
中间位置的计算公式如下:
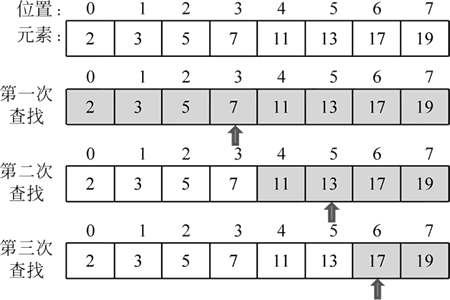
图 1 二分查找算法的工作过程
根据二分查找算法的基本思想,结合上图将该算法的工作过程描述如下。
1) 第一次查找:起始位置为 0,结束位置为 7,中间位置为 (7-0)/2+0≈3,序列中索引位置为 3 的元素是 7。目标值 17 大于 7,则继续查找元素 7 右侧的数据。
2) 第二次查找:起始位置为 4,结束位置为 7,中间位置为 (7-4)/2+4≈5,序列中索引位置为 5 的元素是 13。目标值 17 大于 13,则继续查找元素 13 右侧的数据。
3) 第三次查找:起始位置为 6,结束位置为 7,中间位置为 (7-6)/2+6≈6,序列中索引位置为 6 的元素是 17。正好与目标值 17 相等,则将目标位置 6 返回,整个查找过程结束。
通过分析上述查找过程,将二分查找算法的编程思路描述如下:
【实例】利用二分查找法查找序列 [2,3,5,7,11,13,17,19] 中值为 17 的位置:
因此,折半查找方法适用于不经常变动而查找频繁的有序列表。
二分查找思想
二分查找算法的基本思想:假设序列中的元素是按从小到大的顺序排列的,以序列的中间位置为界将序列一分为二,再将序列中间位置的元素与目标数据比较:- 如果目标数据等于中间位置的元素,则查找成功,结束查找过程;
- 如果目标数据大于中间位置的元素,则在序列的后半部分继续查找;
- 如果目标数据小于中间位置的元素,则在序列中的前半部分继续查找。
当序列不能被定位时,则查找失败,并结束查找过程。
中间位置的计算公式如下:
中间位置≈(结束位置-起始位置)÷2+起始位置
注意,对计算结果进行向下取整。二分查找算法分析

图 1 二分查找算法的工作过程
根据二分查找算法的基本思想,结合上图将该算法的工作过程描述如下。
1) 第一次查找:起始位置为 0,结束位置为 7,中间位置为 (7-0)/2+0≈3,序列中索引位置为 3 的元素是 7。目标值 17 大于 7,则继续查找元素 7 右侧的数据。
2) 第二次查找:起始位置为 4,结束位置为 7,中间位置为 (7-4)/2+4≈5,序列中索引位置为 5 的元素是 13。目标值 17 大于 13,则继续查找元素 13 右侧的数据。
3) 第三次查找:起始位置为 6,结束位置为 7,中间位置为 (7-6)/2+6≈6,序列中索引位置为 6 的元素是 17。正好与目标值 17 相等,则将目标位置 6 返回,整个查找过程结束。
通过分析上述查找过程,将二分查找算法的编程思路描述如下:
- 根据待查找序列的起始位置和结束位置计算出一个中间位置;
- 如果目标数据等于中间位置的元素,则查找成功,返回中间位置;
- 如果目标数据小于中间位置的元素,则在序列的前半部分继续查找;
- 如果目标数据大于中间位置的元素,则在序列的后半部分继续查找;
- 重复进行以上步骤,直到待查找序列的起始位置大于结束位置,即待查找序列不可定位时,则查找失败。
【实例】利用二分查找法查找序列 [2,3,5,7,11,13,17,19] 中值为 17 的位置:
# 返回 x 在 arr 中的索引, 如果不存在则返回 -1
def binarySearch(arr, l, r, x):
# 基本判断
if r >= l:
mid = int(l + (r - l) / 2)
# 元素的中间位置
if arr[mid] == x:
return mid
# 元素小于中间位置的元素, 只需要再比较左边的元素
elif arr[mid] > x:
return binarySearch(arr, l, mid - 1, x)
# 元素大于中间位置的元素, 只需要再比较右边的元素
else:
return binarySearch(arr, mid + 1, r, x)
else:
# 不存在
return -1
# 测试数组
arr = [2, 3, 5, 7, 11, 13, 17, 19]
x = 10
# 函数调用
result = binarySearch(arr, 0, len(arr) - 1, 17)
if result != -1:
print("元素在数组中的索引为 %d" % result)
else:
print("元素不在数组中")
运行程序,输出如下:
元素在数组中的索引为6
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: