LeNet-5实现图像分类（非常详细）

LeNet-5 是一种经典的卷积神经网络，是现代卷积神经网络的起源之一。

下图是 LeNet-5 的经典结构，它一共有 7 层（不包含输入层），分别是 2 个卷积层、2 个池化层和 3 个全连接层（最后一个全连接层为输出层）。

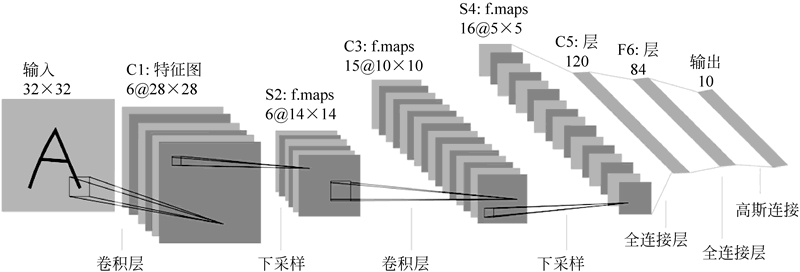
图 1 LeNet-5的经典结构

图 1 的输入是一个 32×32 的图片，通过 6 个 5×5×1 的卷积核对其进行卷积，产生 6 幅 28×28 的卷积特征图，这 6 幅特征图又经过 2×2 的池化提取，变成 6 幅 14×14 的特征图，这样第一个卷积+池化（C1+S2）的操作就完成了，如下图所示。

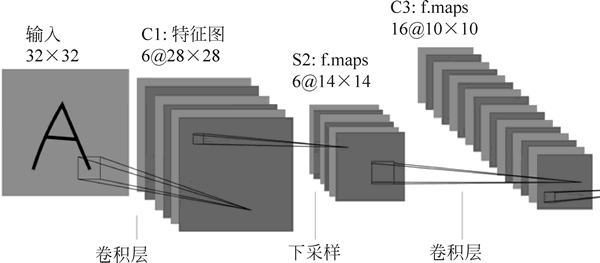
图 2 卷积特征图

接着对这 6 幅 14×14 的特征图使用 16 个 5×5×6 的卷积核进行卷积，产生 16 幅 10×10 的卷积特征图，然后这 16 幅特征图又经过 2×2 的池化提取，变成 16 幅 5×5 的特征图，如下图所示。

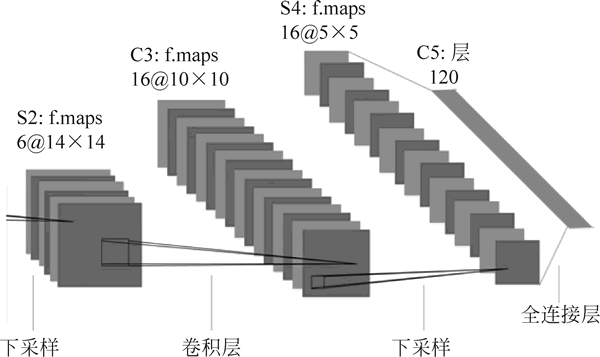
图 3 池化过程

值得一提的是，卷积核不一定是一个二维的矩阵，它也可以是一个三维的卷积核，每个 5×5×6 的卷积核实际执行的操作是同时对 6 幅特征图进行卷积操作，每幅特征图对应一个 5×5×1 的卷积核，最后6幅图卷积的结果再加在一起，等效于一个 5×5×6 的卷积核的卷积结果。

池化后的 16 幅 5×5 的特征图还会经过一次卷积，即 120 个 5×5×16 的卷积核对 16 幅 5×5 的特征图进行卷积，得到 120 幅 1×1 的特征图，这一层也称全连接层，因为每个神经元都与前面的 16 幅特征图相连，实质上这算一次卷积操作，过程如下图所示。

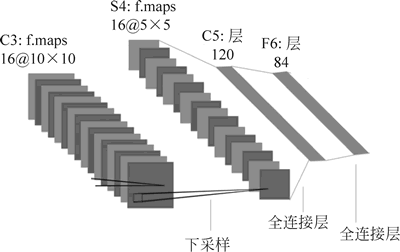
图 4 卷积操作

之后就是一个 120 输入 84 输出的全连接层和一个 84 输入 10 输出的输出层（使用 Softmax 函数激活），如下图所示。

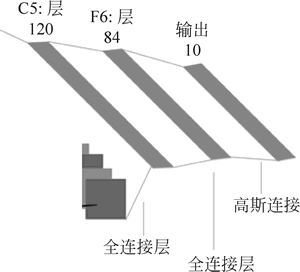
图 5 全连接层与输出层

【实例】使用 LeNet-5 对 MNIST 手写数字图片进行分类。具体实现步骤为：
1) 导入相应的包：

import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import os

2) 定义超参数：

EPOCH=20
BATCH_SIZE=10
LR=0.001
DOWNLOAD_MNIST=False

3) 加载数据集，实例使用 PyTorch 中自带的 MNIST 数据集：

if not os.path.exists('./mnist/') or not os.listdir('./mnist/'):
    DOWNLOAD_MNIST = True

train_data = torchvision.datasets.MNIST(
    root='./mnist/',
    train=True,                         # 训练数据
    transform=torchvision.transforms.ToTensor(),
    # 将 PIL.Image 或 numpy.ndarray 转换为形状为 (C×H×W) 的 torch.FloatTensor
    # 并在 [0.0, 1.0] 范围内归一化
    download=DOWNLOAD_MNIST,
)

train_loader = DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)

test_data = torchvision.datasets.MNIST(
    root='./mnist/',
    train=False,
    transform=torchvision.transforms.ToTensor()
)

test_loader = DataLoader(dataset=test_data, batch_size=BATCH_SIZE, shuffle=True)

4) 定义网络：

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Sequential(
            nn.Conv2d(1, 6, 5),  # 输入通道，输出通道，卷积核大小
            nn.ReLU(),
            nn.MaxPool2d(2),
        )
        self.conv2 = nn.Sequential(
            nn.Conv2d(6, 16, 5),
            nn.ReLU(),
            nn.MaxPool2d(2),
        )
        self.fc1 = nn.Sequential(
            nn.Linear(256, 120),  # 输入特征，输出特征
            nn.ReLU(),
        )
        self.fc2 = nn.Sequential(
            nn.Linear(120, 84),
            nn.ReLU(),
        )
        self.fc3 = nn.Sequential(
            nn.Linear(84, 10),
            nn.ReLU(),
        )

    def forward(self, x):
        x1 = self.conv1(x)
        x2 = self.conv2(x1)
        x2 = x2.view(x.size(0), -1)  # 展开成一维向量，方便后面进行全连接
        x3 = self.fc1(x2)
        x4 = self.fc2(x3)
        x5 = self.fc3(x4)
        return torch.nn.functional.log_softmax(x5, dim=1)

net = Net()
print(net)
Net(
    (conv1): Sequential(
        (0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
        (1): ReLU()
        (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
    )
    (conv2): Sequential(
        (0): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
        (1): ReLU()
        (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
    )
    (fc1): Sequential(
        (0): Linear(in_features=256, out_features=120, bias=True)
        (1): ReLU()
    )
    (fc2): Sequential(
        (0): Linear(in_features=120, out_features=84, bias=True)
        (1): ReLU()
    )
    (fc3): Sequential(
        (0): Linear(in_features=84, out_features=10, bias=True)
        (1): ReLU()
    )
)

代码中，首先输入是大小为 28×28 的单通道图像，用矩阵表示为（Batch，28，28）。

第一个卷积层 Conv1 所用的卷积核尺寸为 55，步长为 1，卷积核数目为 6，那么经过该层后图像尺寸变为 24（28-5+1=24），输出矩阵为（6，24，24）。
第一个池化层 Pool 核尺寸为 22，步长为 2，这是没有重叠的最大池化，池化操作后，图像尺寸减半，变为12×12，输出矩阵为（6，12，12）。
第二个卷积层 Conv2 的卷积核尺寸为 55，步长为 1，卷积核数目为 16，卷积后图像尺寸变为 8，这是因为 12-5+1=8，输出矩阵为（16，8，8）。
第二个池化层 Pool2 核尺寸为 22，步长为 2，这是没有重叠的最大池化，池化操作后，图像尺寸减半，变为 4×4，输出矩阵为（16，4，4）。

Pool2 后面接全连接层 fc1，神经元数目为 120，再接 ReLU 激活函数。fc1 后面接全连接层 fc2，神经元数目为 84，再接 ReLU 激活函数。再接 fc3，神经元个数为 10，得到 10 维的特征向量，用于 10 个数字的分类训练，送入 Softmax 分类，得到分类结果的概率。

5) 开始训练：

loss_func = nn.CrossEntropyLoss()  # 损失函数
optimizer = torch.optim.Adam(net.parameters(), lr=LR)  # 梯度下降
cuda_gpu = torch.cuda.is_available()  # GPU

for epoch in range(EPOCH):
    net.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        if cuda_gpu:
            data, target = data.cuda(), target.cuda()
            net.cuda()

        output = net(data)  # 网络输出结果
        loss = loss_func(output, target)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if (batch_idx + 1) % 400 == 0:
            # --------------------------测试-------------------------
            net.eval()
            correct = 0
            for data, target in test_loader:
                if cuda_gpu:
                    data, target = data.cuda(), target.cuda()
                    net.cuda()
                output = net(data)
                pred = output.data.max(1)[1]  # 获取最大对数概率的索引
                correct += pred.eq(target.data).cpu().sum()
            accuracy = 1. * correct / len(test_loader.dataset)
            print('Epoch:', epoch, '|train loss:%.4f' % loss.data.item(), '|test accuracy: %.2f' % accuracy)

运行结果为：

LeNet-5实现图像分类（非常详细）

相关文章