首页 > 编程笔记 > Python笔记 阅读：554

决策树算法（非常详细，附带实例）

决策树算法通常是一个递归的选择最优特征的过程，并根据该特征对训练数据进行分割，使各个子数据集有一个最好的分类过程。

决策树在进行训练的时候，会使用某种策略（如 ID3 算法）进行最优属性选择，按照最优属性的取值将原始数据集划分为几个数据子集，然后递归地生成一棵决策树。

构建决策树

决策树就是一棵树，一棵决策树包含一个根节点、若干内部节点和若干叶节点：

1) 如何选择测试属性

测试属性（分支属性）的选择顺序影响决策树的结构甚至决策树的准确率（信息增益、信息增益率、Gini 指标）。

2) 如何停止划分样本

从根节点测试属性开始，每个内部节点测试属性都把样本空间划分为若干子区域，一般当某个区域的样本同类时，就停止划分样本，有时也通过阈值提前停止划分样本。

3) 决策树分类的过程

决策树的生成是一个递归过程，在决策树基本算法中，有 3 种情况导致递归返回：
决策树学习的关键是如何选择最优划分属性，一般而言，随着划分过程不断进行，我们希望决策树的分支节点所包含的样本尽可能属于同一类别，即节点的“纯度”越来越高。

① ID3 算法是国际上最有影响力的决策树算法，这种方法就是找出最具有判断力的特征，把数据分为多个子集，每个子集又选择最具判断力的特征进行划分，一直到所有子集都包含同一种类型的数据为止，最后得到一棵决策树。

ID 算法通过对比选择不同特征下数据集的信息增益和香农熵来确定最优划分特征。

香农熵：

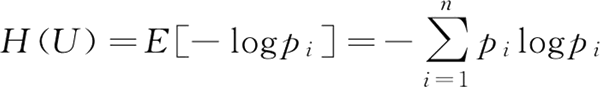
from collections import Counter
import operator
import math
def calcEnt(dataSet):
    classCount = Counter(sample[-1]for sample in dataSet)
    prob = [float(v)/sum(classCount.values())for v in classCount.values()]
    return reduce(operator.add,map(lambda x:-x * math.log(x,2),prob))
纯度差，也称为信息增益，表示为：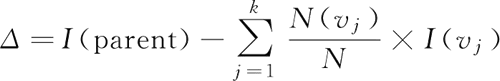


此式实际上就是当前节点的不纯度减去子节点不纯度的加权平均数，权重由子节点记录数与当前节点记录数的比例决定。信息增益越大，则意味着使用属性进行划分所获得的“纯度”提升越大，效果越好。

信息增益准则对可取值数目较多的属性有所偏好。

② C4.5 算法相对于 ID3 算法的重要改进是使用信息增益率来选择节点属性。它克服了 ID3 算法存在的不足：ID3 算法只适用于离散的描述属性，对于连续数据需离散化，而 C4.5 则对离散、连续均能处理。

增益率定义为：


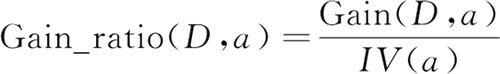
其中：


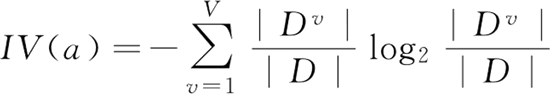
需注意的是，增益率准则对可取值数目较少的属性有所偏好。因此，C4.5 算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

③ CART 算法使用“基尼指数”来选择划分属性，数据集 D 的纯度可用基尼值来度量：


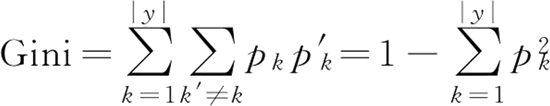
它反映了从数据集 D 中随机抽取两个样本，其类别标记不一致的概率。因此 Gini(D) 越小，则数据集 D 的纯度越高。
from collections import Counter
import operator
　　　　　
def calcGini(dataSet):
    labelCounts = Counter(sample[-1]for sample in dataSet)
    prob = [float(v)/sum(labelCounts.values())for v in labelCounts.values()]
    return 1-reduce(operator.add,map(lambda x:x * * 2,prob))

为避免过拟合，需要对生成树剪枝。决策树剪枝的基本策略有“预剪枝”和“后剪枝”：

决策树实战

前面已介绍决策树的原理、构建等相关内容，下面直接通过决策树对导入的红酒数据集进行分析。

【实例】利用决策树分析红酒数据集。 
#导入tree模块
from sklearn import tree
#导入红酒数据集,数据集包含来自3种不同起源的葡萄酒的共178条记录
#13个属性是葡萄酒的13种化学成分,通过化学分析可推断葡萄酒的起源,起源为3个产地
#所有属性变量都是连续变量
from sklearn.datasets import load_wine
#导入训练集和测试集切分包
from sklearn.model_selection import train_test_split
import pandas as pd
#红酒数据集的数据探索
wine = load_wine()
print('x数据集形状:',wine.data.shape)
print('y数据集形状:',wine.target.shape)
#将x,y都放到数据集data_frame中
data_frame = pd.concat([pd.DataFrame(wine.data),pd.DataFrame(wine.target)],axis = 1)
#显示前10行
print('数据前十行显示:\n',data_frame.head(10))
#显示数据集特征列名
print('数据集特征列名:',wine.feature_names)
#显示数据集的标签分类
print('数据集标签分类:',wine.target_names)
# 70 %为训练数据,30%为测试数据
Xtrain,Xtest,Ytrain,Ytest = train_test_split(wine.data,wine.target,test_size = 0.3)
print('训练数据的大小为:',Xtrain.shape)
print('测试数据的大小为:',Xtest.shape)
#初始化树模型,criterion:gini或者entropy,前者是基尼系数,后者是信息熵
clf = tree.DecisionTreeClassifier(criterion = "entropy")
#实例化训练集
clf = clf.fit(Xtrain,Ytrain)
#返回测试集的准确度
score = clf.score(Xtest,Ytest)
y = clf.predict(Xtest)
print('测试集的准确度:',score)
for each in range(len(Ytest)):
    print('预测结果:',y[each],'\t真实结果:',Ytest[each],'\n')
#特征重要性
feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类',\
                  '花青素','颜色强度','色调','od280/od315稀释葡萄酒','脯氨酸']
print(clf.feature_importances_)
print([ * zip(feature_name,clf.feature_importances_)])
运行程序，输出如下：

x数据集形状:(178,13)
y数据集形状:(178,)
数据前十行显示:
0　　 1　　 2　　 3　　　4　　 5　　 6 　  7　   8　　 9　　 10　　11　\
0　14.23　1.71　2.43　15.6　127.0　2.80　3.06　0.28　2.29　5.64　1.04　3.92
1　13.20　1.78　2.14　11.2　100.0　2.65　2.76　0.26　1.28　4.38　1.05　3.40
2　13.16　2.36　2.67　18.6　101.0　2.80　3.24　0.30　2.81　5.68　1.03　3.17
3　14.37　1.95　2.50　16.8　113.0　3.85　3.49　0.24　2.18　7.80　0.86　3.45
4　13.24　2.59　2.87　21.0　118.0　2.80　2.69　0.39　1.82　4.32　1.04　2.93
5　14.20　1.76　2.45　15.2　112.0　3.27　3.39　0.34　1.97　6.75　1.05　2.85
6　14.39　1.87　2.45　14.6　 96.0　2.50　2.52　0.30　1.98　5.25　1.02　3.58
7　14.06　2.15　2.61　17.6　121.0　2.60　2.51　0.31　1.25　5.05　1.06　3.58
8　14.83　1.64　2.17　14.0　 97.0　2.80　2.98　0.29　1.98　5.20　1.08　2.85
9　13.86　1.35　2.27　16.0　 98.0　2.98　3.15　0.22　1.85　7.22　1.01　3.55
        12　 0
0　1065.0　  0
1　1050.0　  0
2　1185.0　  0
3　1480.0　  0
4　 735.0　  0
5　1450.0　  0
6　1290.0　  0
7　1295.0　  0
8　1045.0　  0
9　1045.0　  0
数据集特征列名:['alcohol','malic_acid','ash','alcalinity_of_ash','magnesium','total_phenols','flavanoids','nonflavanoid_phenols','proanthocyanins','color_intensity','hue','od280/od315_of_diluted_wines','proline']
数据集标签分类:['class_0''class_1''class_2']
训练数据的大小为:(124,13)
测试数据的大小为:(54,13)
测试集的准确度:0.962962962963
…　　　　　　　…
预测结果:0　真实结果:0
预测结果:1　真实结果:1
预测结果:0　真实结果:0
预测结果:1　真实结果:1
预测结果:0　真实结果:0
[0.　　　　　0.01789104　0.　　　　　0.　　　　　0.01658185　0.　　　　　0.46220527 0.　　　　　0.　　　　　0.18773294　0.　　　　　0.           0.31558891]
[('酒精',0.0),('苹果酸',0.017891036487245639),('灰',0.0),('灰的碱性',0.0),('镁',0.016581845458501384),('总酚',0.0),('类黄酮',0.46220526817493346),('非黄烷类酚类',0.0),('花青素',0.0),('颜色强度',0.18773293638314775),('色调',0.0),('od280/od315稀释葡萄酒',0.0),('脯氨酸',0.3155889134961718)]

决策树的优势与不足

与其他算法相比，决策树有其自身的优势与不足。

决策树的优势主要表现在：
决策树的不足主要表现在：
为了避免过拟合的问题出现，可以使用集合学习的方法，也就是下面要介绍的随机森林算法。

相关文章