决策树算法详解(Python实现)
决策树(decision tree)是一个类似于流程图的树状结构,树内部的每一个节点代表的是对一个特征的测试,树的分支代表特征的每一个测试结果,树的叶节点代表一种分类结果。
决策树模型既可以做分类也可以做回归。它的一个优点是,如果处理非线性数据,它不需要对特征进行任何转换。因为决策树一次只分析一个特征,而不考虑加权组合。同样,决策树也不需要归一化或标准化函数。
当用决策树进行分类时,定义熵作为杂质的指标以确定采用哪个特征分裂可以最大化信息增益(Information Gain,IG)。二进制分裂定义为:
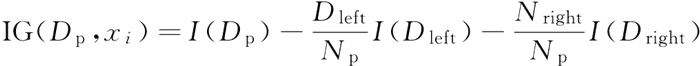
其中,xi 为要分裂的样本特征,Np 为父节点的样本数,I 为杂质函数,Dp 为父节点训练样本的子集。Dleft 和 Dright 为分裂后左、右两个子节点的训练样本集。
决策树的目标是找到可以最大化信息增益的特征分裂,即希望找到可以减少子节点中杂质的分裂特征。为了把回归决策树用于回归,需要一个适合连续变量的杂质指标,即把节点 t 的杂质指标定义为 MSE:
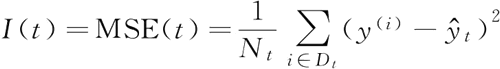
其中,Nt 为节点 t 的训练样本数,Dt 为节点 t 的训练数据子集,y(i) 为真实的目标值,为预测的目标值(样本均值)。
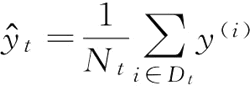
在决策树回归的背景下,通常也把 MSE 称为内节点方差(within-node variance),这就是也把分裂标准称为方差缩减(variance reduction)的原因。
【实例】决策树的实现。
下表为训练数据集,特征向量只有一维,根据此数据表建立回归决策树。
1) 选择最优切分变量j与最优切分点 s:在本数据集中,只有一个特征变量,最优切分变量自然是 x。接下来考虑 9 个切分点 {1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5}(切分变量两个相邻取值为区间 [ai,ai+1) 内任一点均可),计算每个待切分点的损失函数值。损失函数为:
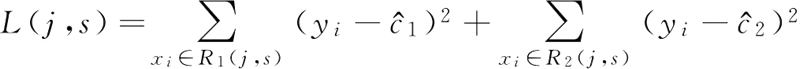
其中:
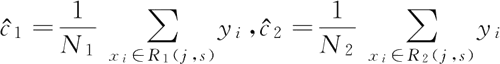
① 计算子区域输出值。当 s=1.5 时,两个子区域 R1={1},R2={2,3,4,5,6,7,8,9,10},c1=5.56,c2=(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)/9=7.5。
得到其他各切分点的子区域输出值,列表如下:
② 计算损失函数值,找到最优切分点。当 s=1.5 时:
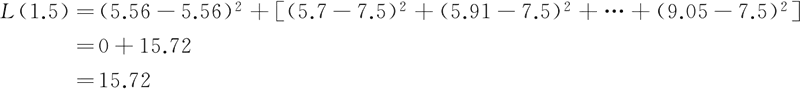
计算得到其他各切分点的损失函数值,列表如下:
③ 易知,取 s=6.5 时,损失函数值最小。因此,第一个划分点为(j=x,s=6.5)。
2) 用选定的对(j,s)划分区域并决定相应的输出值。
划分区域:R1={1,2,3,4,5},R2={7,8,9,10}。
对应输出值:c1=6.24,c2=8.91。
3) 调用步骤 1)、2),继续划分。
对 R1,取划分点 {1.5,2.5,3.5,4.5,5.5},计算得到单元输出值为:
损失函数值为:
L(3.5) 最小,取 s=3.5 为划分点。后面以此类推。
4) 生成回归树。
假设两次划分后即停止,则最终生成的回归树为:
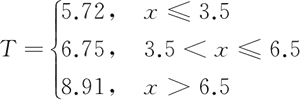
以下利用 Python 实现与线性回归对比:
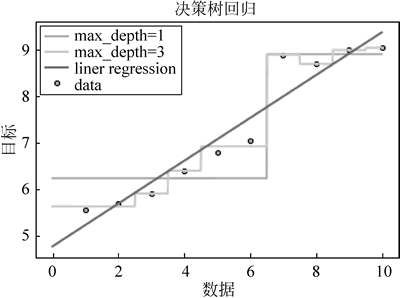
图 8 决策树回归
决策树模型既可以做分类也可以做回归。它的一个优点是,如果处理非线性数据,它不需要对特征进行任何转换。因为决策树一次只分析一个特征,而不考虑加权组合。同样,决策树也不需要归一化或标准化函数。
当用决策树进行分类时,定义熵作为杂质的指标以确定采用哪个特征分裂可以最大化信息增益(Information Gain,IG)。二进制分裂定义为:
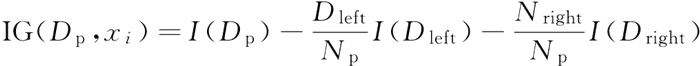
其中,xi 为要分裂的样本特征,Np 为父节点的样本数,I 为杂质函数,Dp 为父节点训练样本的子集。Dleft 和 Dright 为分裂后左、右两个子节点的训练样本集。
决策树的目标是找到可以最大化信息增益的特征分裂,即希望找到可以减少子节点中杂质的分裂特征。为了把回归决策树用于回归,需要一个适合连续变量的杂质指标,即把节点 t 的杂质指标定义为 MSE:
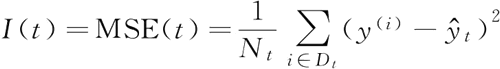
其中,Nt 为节点 t 的训练样本数,Dt 为节点 t 的训练数据子集,y(i) 为真实的目标值,为预测的目标值(样本均值)。
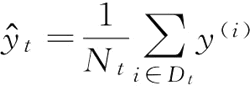
在决策树回归的背景下,通常也把 MSE 称为内节点方差(within-node variance),这就是也把分裂标准称为方差缩减(variance reduction)的原因。
【实例】决策树的实现。
下表为训练数据集,特征向量只有一维,根据此数据表建立回归决策树。
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 5.56 | 5.7 | 5.91 | 6.4 | 6.8 | 7.05 | 8.9 | 8.7 | 9 | 9.05 |
1) 选择最优切分变量j与最优切分点 s:在本数据集中,只有一个特征变量,最优切分变量自然是 x。接下来考虑 9 个切分点 {1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5}(切分变量两个相邻取值为区间 [ai,ai+1) 内任一点均可),计算每个待切分点的损失函数值。损失函数为:
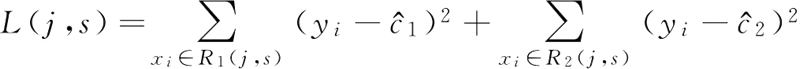
其中:
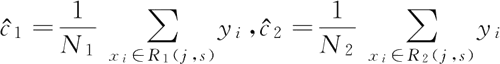
① 计算子区域输出值。当 s=1.5 时,两个子区域 R1={1},R2={2,3,4,5,6,7,8,9,10},c1=5.56,c2=(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)/9=7.5。
得到其他各切分点的子区域输出值,列表如下:
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
| c_(1) | 5.56 | 5.63 | 5.72 | 5.89 | 6.07 | 6.24 | 6.62 | 6.88 | 7.11 |
| c_(2) | 7.5 | 7.73 | 7.99 | 8.25 | 8.54 | 8.91 | 8.92 | 9.03 | 9.05 |
② 计算损失函数值,找到最优切分点。当 s=1.5 时:
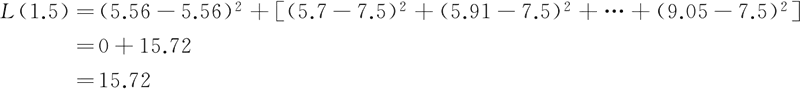
计算得到其他各切分点的损失函数值,列表如下:
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
| L(s) | 15.72 | 12.07 | 8.36 | 5.78 | 3.91 | 1.93 | 8.01 | 11.73 | 15.74 |
③ 易知,取 s=6.5 时,损失函数值最小。因此,第一个划分点为(j=x,s=6.5)。
2) 用选定的对(j,s)划分区域并决定相应的输出值。
划分区域:R1={1,2,3,4,5},R2={7,8,9,10}。
对应输出值:c1=6.24,c2=8.91。
3) 调用步骤 1)、2),继续划分。
对 R1,取划分点 {1.5,2.5,3.5,4.5,5.5},计算得到单元输出值为:
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 |
| c_(1) | 5.56 | 5.63 | 5.72 | 5.89 | 6.07 |
| c_(2) | 6.37 | 5.54 | 6.75 | 6.93 | 7.05 |
损失函数值为:
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 |
| L(s) | 1.3087 | 0.754 | 0.2771 | 0.4368 | 1.0644 |
L(3.5) 最小,取 s=3.5 为划分点。后面以此类推。
4) 生成回归树。
假设两次划分后即停止,则最终生成的回归树为:
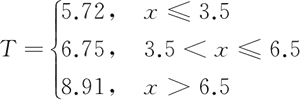
以下利用 Python 实现与线性回归对比:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn import linear_model
# 支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 1. 数据集
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05]).ravel()
# 2. 拟合三种模型
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = linear_model.LinearRegression()
model1.fit(x, y)
model2.fit(x, y)
model3.fit(x, y)
# 3. 预测(连续曲线)
X_test = np.arange(0.0, 10.0, 0.01)[:, np.newaxis]
y_1 = model1.predict(X_test)
y_2 = model2.predict(X_test)
y_3 = model3.predict(X_test)
# 4. 绘图
plt.figure()
plt.scatter(x, y, s=20, edgecolor='black', c='darkorange', label='data')
plt.plot(X_test, y_1, color='cornflowerblue', label='max_depth=1', linewidth=2)
plt.plot(X_test, y_2, color='yellowgreen', label='max_depth=3', linewidth=2)
plt.plot(X_test, y_3, color='red', label='linear regression', linewidth=2)
plt.xlabel('数据')
plt.ylabel('目标')
plt.title('决策树回归')
plt.legend()
plt.show()
运行程序,效果如下图所示:
图 8 决策树回归
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: