卷积神经网络详解(Python实现)
卷积神经网络(convolutional neural networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络(feedforward neural networks,FNN),是深度学习的代表算法之一。
由于卷积神经网络具有表征学习的能力,能够按其阶层结构对输入信息进行平移不变分类,因此也被称为平移不变人工神经网络(shift-invariant artificial neural networks,SIANN)。
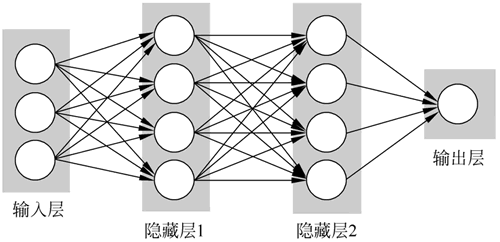
图 1 神经网络结构
那卷积神经网络跟它是什么关系呢?其实卷积神经网络依旧是层级网络,只是层的功能和形式发生了变化,可以说是传统神经网络的一个改进,其结构如下图所示。
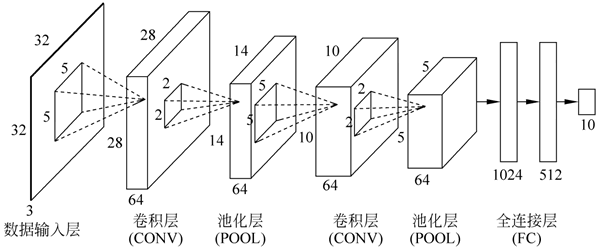
图 2 卷积神经网络结构
从图 2 中可看出,典型的 CNN 模型层次主要包括:数据输入层、卷积层、池化层和全连接层。下图中就多了许多传统神经网络没有的层次。
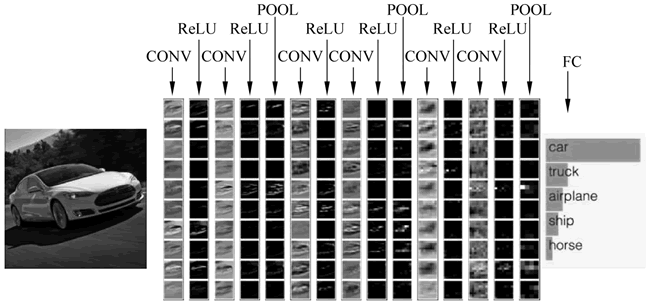
图 3 包含完整层次的CNN结构
去均值与归一化效果如下图所示:
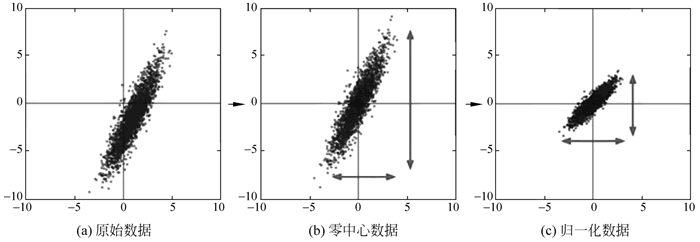
图 4 去均值与归一化效果
去相关与白化效果如下图所示:
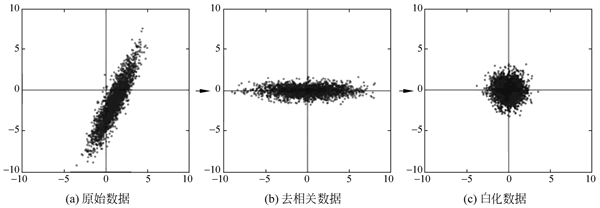
图 5 去相关与白化效果
下面借助一个例子来理解这一点。为简单起见,将采用具有归一化像素的二维输入图像,如下图所示。
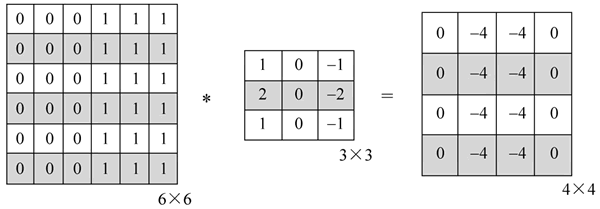
图 6 二维输入图像
在图 6 中,有一个大小为 6×6 的输入图像,对其应用了一个 3×3 的过滤器,结果得到了一个 4×4 的特征图,其中包含有关输入图像的一些信息。
下面将深入了解获取输入图像中特征图的一些数学原理。
如下图所示,第一步过滤器应用于图像的灰色部分,将图像的像素值与过滤器的值相乘(如图中使用线条所示),然后相加得到最终值。
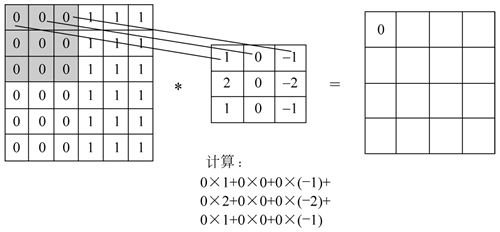
图 7 第一步过滤器
接着,过滤器将移动一列,如下图所示。这种跳转到下一列或行的过程称为 stride,在实例中,将 stride 设为 1,这意味着将移动一列。
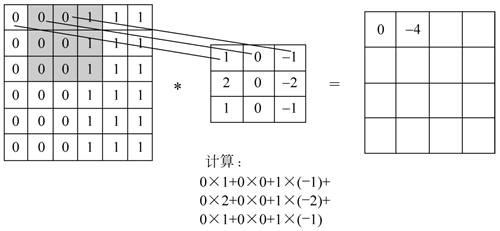
图 8 移动一列效果
类似地,过滤器通过整个图像,得到最终的特征图,如下图所示。一旦获得特征图,就会对其应用激活函数来引入非线性。
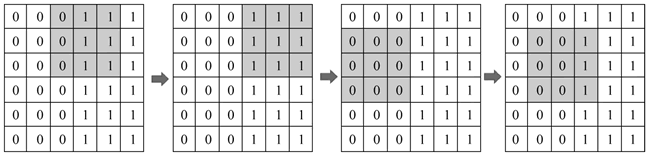
图 9 特征图
这里需要注意的一点是,得到的特征图的大小小于图像的大小。随着增加 stride 的值,特征图的大小会减小。
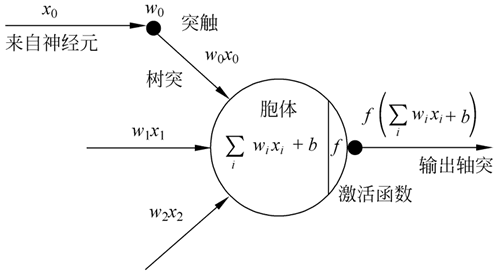
图 10 非线性映射
CNN 采用的激励函数一般为 ReLU(the rectified linear unit,修正线性单元),它的特点是收敛快、求梯度简单,但较脆弱,其图像如下图所示。
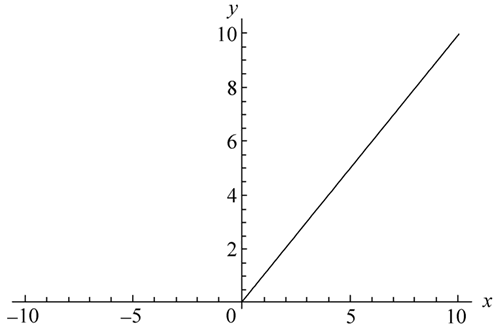
图 11 ReLU激励函数
使用池化,可以创建一个较低分辨率的输入版本,该版本仍然包含输入图像的大元素或重要元素。
最常见的池化类型是最大池化和平均池化。下图显示了最大池化的工作原理。
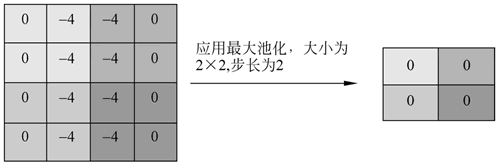
图 12 最大池化
使用从上面例子中得到的特征图来应用池化。这里使用了一个大小为 2×2 的池化层,步长为 2。
取每个突出显示区域的最大值,并获得大小为 2×2 的新版本输入图像,因此在应用池化后,特征图的维数减少了。
CNN 模型的完整过程可以在下图中看到:
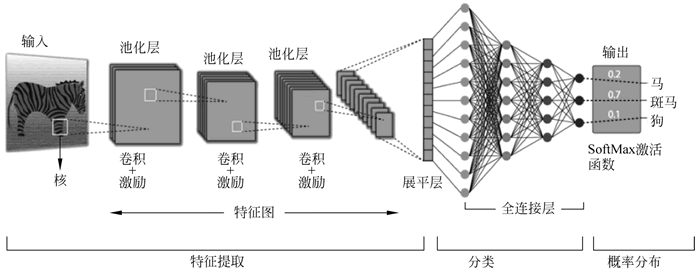
图 13 CNN模型的完整过程
向前传播过程:
在此阶段,信息从输入层经过逐层变换,传送到输出层,输出层与每层的权值矩阵点乘,得到输出结果。
向后传播阶段:
【实例】卷积神经网络的手写数字模型实例。实现步骤如下:
1) 引入头文件,加载数据。
2) 封装函数,方便网络搭建多处调用。
① 构建权重 w,产生随机变量:
② 构建偏置 b:
③ 卷积层准备,卷积函数实现:
④ 卷积层,激活函数 x 与 0 作比较:
⑤ 池化层,小一半数据特征图:
3) 特征标签的占位符
4) 开始网络搭建 CNN 构建
① 卷积层,创建 patch=5×5 卷积核,并且构建 w、b:
第一层卷积层,调用函数:
激励层 ReLU:
池化层:
② 第二层卷积。和第一层差不多,但需要注意几个点:
③ 全连接层。实现数据排平、提纯、分类。
第一层全连接层,前馈神经网络输入。假设神经元为 1024 个:
第二层全连接层,分类器。上一层的输出是这一层的输入,总的分类数为这一层的输出:
由于卷积神经网络具有表征学习的能力,能够按其阶层结构对输入信息进行平移不变分类,因此也被称为平移不变人工神经网络(shift-invariant artificial neural networks,SIANN)。
从神经网络到卷积神经网络
从前面学习可知,神经网络的结构如下图所示:
图 1 神经网络结构
那卷积神经网络跟它是什么关系呢?其实卷积神经网络依旧是层级网络,只是层的功能和形式发生了变化,可以说是传统神经网络的一个改进,其结构如下图所示。

图 2 卷积神经网络结构
从图 2 中可看出,典型的 CNN 模型层次主要包括:数据输入层、卷积层、池化层和全连接层。下图中就多了许多传统神经网络没有的层次。

图 3 包含完整层次的CNN结构
1) 数据输入层
该层要做的处理主要是对原始图像数据进行预处理,其中包括:- 去均值:把输入数据各个维度都中心化为 0,其目的就是把样本的中心拉回到坐标系原点上;
- 归一化:幅度归一化到同样的范围,即减少各维度数据取值范围的差异而带来的干扰。例如,我们有两个维度的特征 A 和 B, A 范围是 0~10,而 B 范围是 0~10000,如果直接使用这两个特征是有问题的,好的做法就是归一化,即 A 和 B 的数据都变为 0~1 的范围;
- PCA(去相关)/白化:用 PCA 降维;白化是对数据各个特征轴上的幅度归一化。
去均值与归一化效果如下图所示:

图 4 去均值与归一化效果
去相关与白化效果如下图所示:

图 5 去相关与白化效果
2) 卷积层
卷积层是将过滤器应用于输入图像以提取或检测其特征的层。过滤器多次应用于图像并创建一个有助于对输入图像进行分类的特征图。下面借助一个例子来理解这一点。为简单起见,将采用具有归一化像素的二维输入图像,如下图所示。
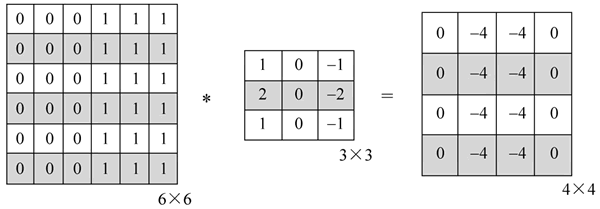
图 6 二维输入图像
在图 6 中,有一个大小为 6×6 的输入图像,对其应用了一个 3×3 的过滤器,结果得到了一个 4×4 的特征图,其中包含有关输入图像的一些信息。
下面将深入了解获取输入图像中特征图的一些数学原理。
如下图所示,第一步过滤器应用于图像的灰色部分,将图像的像素值与过滤器的值相乘(如图中使用线条所示),然后相加得到最终值。

图 7 第一步过滤器
接着,过滤器将移动一列,如下图所示。这种跳转到下一列或行的过程称为 stride,在实例中,将 stride 设为 1,这意味着将移动一列。

图 8 移动一列效果
类似地,过滤器通过整个图像,得到最终的特征图,如下图所示。一旦获得特征图,就会对其应用激活函数来引入非线性。

图 9 特征图
这里需要注意的一点是,得到的特征图的大小小于图像的大小。随着增加 stride 的值,特征图的大小会减小。
3) ReLU激励层
对卷积层的输出结果做非线性映射,如下图所示:
图 10 非线性映射
CNN 采用的激励函数一般为 ReLU(the rectified linear unit,修正线性单元),它的特点是收敛快、求梯度简单,但较脆弱,其图像如下图所示。

图 11 ReLU激励函数
4) 池化层
池化层应用在卷积层之后,用于降低特征图的维度,有助于保留输入图像的重要信息或特征,并减少计算时间。使用池化,可以创建一个较低分辨率的输入版本,该版本仍然包含输入图像的大元素或重要元素。
最常见的池化类型是最大池化和平均池化。下图显示了最大池化的工作原理。

图 12 最大池化
使用从上面例子中得到的特征图来应用池化。这里使用了一个大小为 2×2 的池化层,步长为 2。
取每个突出显示区域的最大值,并获得大小为 2×2 的新版本输入图像,因此在应用池化后,特征图的维数减少了。
5) 全连接层
到目前为止,已经执行了特征提取步骤,现在是分类部分。全连接层用于将输入图像分类为标签。该层将从前面的步骤(即卷积层和池化层)中提取的信息连接到输出层,并最终将输入分类为所需的标签。CNN 模型的完整过程可以在下图中看到:

图 13 CNN模型的完整过程
Python实现卷积神经网络
卷积神经网络算法过程主要分两个阶段:向前传播和向后传播。向前传播过程:
- 从样本中读取(x,y),将 x 输入网络;
- 计算相应的实际输出 OP。
在此阶段,信息从输入层经过逐层变换,传送到输出层,输出层与每层的权值矩阵点乘,得到输出结果。
向后传播阶段:
- 计算实际输出与理想输出的差值;
- 按极小误差反向传播调整权值矩阵。
【实例】卷积神经网络的手写数字模型实例。实现步骤如下:
1) 引入头文件,加载数据。
import tensorflow as tf
#加载数据
from tensorflow.examples.tutorials.mnist import input_data
#将数据读入数据集:独热编码
input_data.read_data_sets('MNIST_data/',one_hot = True)
input_size = 28 * 28
#分类
num_class = 10
2) 封装函数,方便网络搭建多处调用。
① 构建权重 w,产生随机变量:
#创建函数:构建权重w,产生随机变量
def weight_variable(shape):
w = tf.random_normal(shape = shape,stddev = 0.01)
return tf.Variable(w)
② 构建偏置 b:
def bias_variable(shape):
b = tf.constant(0.01,shape = shape)
return tf.Variable(b)
③ 卷积层准备,卷积函数实现:
def con2d(x,w):
"""
:param x:图像矩阵信息
:param w:卷积核的值
"""
#strides:卷积步长[上、右、下、左]
return tf.nn.conv2d(x,w,strides = [1,1,1,1],padding = 'SAME')
④ 卷积层,激活函数 x 与 0 作比较:
def relu_con(x):
return tf.nn.relu(x)
⑤ 池化层,小一半数据特征图:
def max_pool_con2x2(x):
"""
池化层:小一半数据特征图
:param x:图片的矩阵信息
:return:
value,
ksize,
strides
padding,
data_format = "NHWC",
name = None,
input = None
"""
return tf.nn.max_pool(x,ksize = [1,2,2,1],strides = [1,2,2,1],padding = 'SAME')
3) 特征标签的占位符
#占位符——输入层x:数据输入到图中进行计算;y:识别的数字,有几个类别输入几个数字 xs = tf.placeholder(tf.float32,shape = [None,input_size]) #64列不知道几行 ys = tf.placeholder(tf.float32,shape = [None,num_class]) #10类不知道多少个
4) 开始网络搭建 CNN 构建
① 卷积层,创建 patch=5×5 卷积核,并且构建 w、b:
#第一层:卷积层.创建patch = 5×5卷积核 #([卷积核大小5×5,输入数据的维度1(灰度处理),输出的高度32]) #构建w\b w_conv1 = weight_variable([5,5,1,32]) b_conv1 = bias_variable([32])
第一层卷积层,调用函数:
conv1 = con2d(x_image,w_conv1)
激励层 ReLU:
h_conv1 = relu_con(conv1 + b_conv1)
池化层:
h_pool1 = max_pool_con2x2(h_conv1)
② 第二层卷积。和第一层差不多,但需要注意几个点:
#第二层:卷积层.创建patch = 5×5卷积核 #([卷积核大小5×5,输入数据的维度1(灰度处理),输出的高度32]) #构建w\b,上一层的输出是这一层的输入 w_conv2 = weight_variable([5,5,32,64]) b_conv2 = bias_variable([64]) #第一层卷积层(上一层池化的结果,这一层的w) conv2 = con2d(h_pool1,w_conv2) #激励层ReLU h_conv2 = relu_con(conv2 + b_conv2) #池化层 h_pool2 = max_pool_con2x2(h_conv2)
③ 全连接层。实现数据排平、提纯、分类。
第一层全连接层,前馈神经网络输入。假设神经元为 1024 个:
w_fc1 = weight_variable([7 * 7 * 64,1024]) b_fc1 = bias_variable([1024]) #输出矩阵:行(不定),列:7×7×64 h_pool2_flat = tf.reshape(h_pool2,[-1,7 * 7 * 64]) #前馈神经网络wx + b h_fc1 = tf.matmul(h_pool2_flat,w_fc1) + b_fc1 #激活 h_flc1 = relu_con(h_fc1)
第二层全连接层,分类器。上一层的输出是这一层的输入,总的分类数为这一层的输出:
w_fc2 = weight_variable([1024,num_class]) b_fc2 = bias_variable([num_class]) #计算并激励 #前馈神经网络wx + b h_fc2 = tf.matmul(h_flc1,w_fc2) + b_fc2 #激励——分类,返回每种情况的概率 predict = h_flc2 = tf.nn.softmax(h_fc2)
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: