贪心算法详解(附带实例,C++实现)
贪心算法总是做出当前最优选择,期望通过局部最优选择得到全局最优解。
贪心算法正是“活在当下,看清楚眼前”的算法,从问题的初始解开始,一步一步地做出当前最优选择,逐步逼近目标,尽可能得到最优解;即使得不到最优解,也可以得到最优解的近似解。
贪心算法在解决问题的策略上看似“目光短浅”,即只根据当前已有的信息做出选择,而且一旦做出选择,则不管将来有什么结果,都不会改变。换言之,贪心算法并未考虑全局最优,只是考虑了某种意义上的局部最优。
贪心算法在生活、生产中被广泛应用,对许多问题都可以使用贪心算法得到全局最优解或全局最优解的近似解。
应用同一规则,先将原问题变为一个相似的但规模更小的子问题,之后的每一步都是当前最优选择。当前选择只依赖已做出的选择,不依赖未做出的选择。贪心算法在解决问题时无回溯过程。
例如,原问题 S={a1,a2,…,ai,…,an},通过贪心选择选出一个当前最优解{ai}之后,求解原问题被转换为求解子问题 S-{ai},若原问题的最优解包含子问题的最优解,则说明该问题具有最优子结构性质。
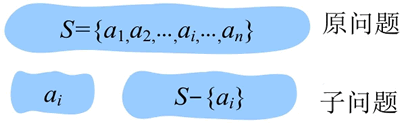
贪心算法的求解步骤如下:
1) 确定贪心策略,选择当前看上去最好的一个。例如挑选苹果,若你认为最大的苹果是最好的,则每次都从苹果堆中拿一个最大的苹果作为局部最优解,贪心策略就是选择当前最大的苹果。若你认为最红的苹果是最好的,则每次都从苹果堆中拿一个最红的苹果,贪心策略就是选择当前最红的苹果。因此求解目标不同,贪心策略也会不同。
2) 根据贪心策略,一步步地得到局部最优解。例如第 1 次选择一个最大的苹果,记为 a1;第 2 次再从剩下的苹果中选择一个最大的苹果,记为 a2,以此类推。对所有的局部最优解进行合并,即可得到原问题的最优解 {a1,a2,…}。
要求装载的古董尽可能多,而海盗船的载重是固定的,则优先装入重量小的古董,在海盗船的载重固定的情况下,装入的古董最多。可以使用重量最小者先装入的贪心策略,从局部最优达到全局最优,从而得到最优装载问题的最优解。
首先把 n 个古董按重量从小到大排序,然后根据贪心策略尽可能多地选择前i个古董装入,直到不能继续装入时为止。此时装入的古董数量就是全局最优解。
每个古董的重量如下表所示,海盗船的载重 c 为 30,在不打碎古董又不超过载重的情况下,怎样才能装入最多的古董?

因为贪心策略是每次都选择重量最小的古董装入海盗船,所以可以将古董按重量从小到大排序,排序后如下表所示。

根据贪心策略及排序后的结果,每次都选择重量最小的古董装入:
即装入古董的数量为 5(ans=5)。
① 按重量排序。可以利用 C++ 中的排序函数 sort() 对古董按重量从小到大排序。要使用此函数,只需引入头文件:
② 根据贪心策略找最优解。首先用变量 ans 记录已装载的古董数量,tmp 代表已装载的古董重量,将两个变量都初始化为 0;然后在排序的基础上,依次检查每个古董的重量,使 tmp 加上该古董的重量,若其结果小于或等于载重 c,则令 ans++,否则退出。
空间复杂度:使用了 tmp、ans 等辅助变量,空间复杂度为 O(1)。
贪心算法正是“活在当下,看清楚眼前”的算法,从问题的初始解开始,一步一步地做出当前最优选择,逐步逼近目标,尽可能得到最优解;即使得不到最优解,也可以得到最优解的近似解。
贪心算法在解决问题的策略上看似“目光短浅”,即只根据当前已有的信息做出选择,而且一旦做出选择,则不管将来有什么结果,都不会改变。换言之,贪心算法并未考虑全局最优,只是考虑了某种意义上的局部最优。
贪心算法在生活、生产中被广泛应用,对许多问题都可以使用贪心算法得到全局最优解或全局最优解的近似解。
贪心算法实现思路
对哪些问题可以使用贪心算法,对哪些问题不可以使用贪心算法呢?若问题具有两个特性,即贪心选择和最优子结构,则可以使用贪心算法。1) 贪心选择
贪心选择指的是可以通过一系列局部最优选择得到原问题的全局最优解。应用同一规则,先将原问题变为一个相似的但规模更小的子问题,之后的每一步都是当前最优选择。当前选择只依赖已做出的选择,不依赖未做出的选择。贪心算法在解决问题时无回溯过程。
2) 最优子结构
最优子结构指的是原问题的最优解包含其子问题的最优解。是否具有最优子结构性质是能否使用贪心算法求解的关键。例如,原问题 S={a1,a2,…,ai,…,an},通过贪心选择选出一个当前最优解{ai}之后,求解原问题被转换为求解子问题 S-{ai},若原问题的最优解包含子问题的最优解,则说明该问题具有最优子结构性质。
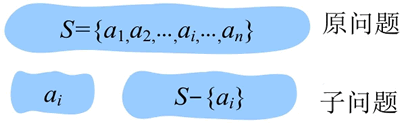
贪心算法的求解步骤如下:
1) 确定贪心策略,选择当前看上去最好的一个。例如挑选苹果,若你认为最大的苹果是最好的,则每次都从苹果堆中拿一个最大的苹果作为局部最优解,贪心策略就是选择当前最大的苹果。若你认为最红的苹果是最好的,则每次都从苹果堆中拿一个最红的苹果,贪心策略就是选择当前最红的苹果。因此求解目标不同,贪心策略也会不同。
2) 根据贪心策略,一步步地得到局部最优解。例如第 1 次选择一个最大的苹果,记为 a1;第 2 次再从剩下的苹果中选择一个最大的苹果,记为 a2,以此类推。对所有的局部最优解进行合并,即可得到原问题的最优解 {a1,a2,…}。
贪心算法解决最优装载问题
有一天,海盗们截获了一艘装满各式各样古董的货船,每件古董都价值连城,但古董一旦被打碎,就失去了价值。虽然海盗船足够大,但载重为c,每件古董的重量都为wi,海盗们绞尽脑汁也要把尽可能多的古董装上海盗船,这时该怎么办呢?1) 问题分析
本题为最优装载问题,可以尝试使用贪心算法求解。要求装载的古董尽可能多,而海盗船的载重是固定的,则优先装入重量小的古董,在海盗船的载重固定的情况下,装入的古董最多。可以使用重量最小者先装入的贪心策略,从局部最优达到全局最优,从而得到最优装载问题的最优解。
2) 算法设计
当海盗船的载重为定值 c 时,wi 越小,可装载的古董数量n越大。依次选择最小重量的古董装入,直到不能继续装入时为止。首先把 n 个古董按重量从小到大排序,然后根据贪心策略尽可能多地选择前i个古董装入,直到不能继续装入时为止。此时装入的古董数量就是全局最优解。
每个古董的重量如下表所示,海盗船的载重 c 为 30,在不打碎古董又不超过载重的情况下,怎样才能装入最多的古董?

因为贪心策略是每次都选择重量最小的古董装入海盗船,所以可以将古董按重量从小到大排序,排序后如下表所示。

根据贪心策略及排序后的结果,每次都选择重量最小的古董装入:
- i=0:选择第 1 个古董装入,tmp=2,不超过载重 30,ans=1;
- i=1:选择第 2 个古董装入,tmp=2+3=5,不超过载重 30,ans=2;
- i=2:选择第 3 个古董装入,tmp=5+4=9,不超过载重 30,ans=3;
- i=3:选择第 4 个古董装入,tmp=9+5=14,不超过载重 30,ans=4;
- i=4:选择第 5 个古董装入,tmp=14+7=21,不超过载重 30,ans=5;
- i=5:选择第 6 个古董装入,tmp=21+10=31,超过载重 30,结束。
即装入古董的数量为 5(ans=5)。
3) 算法实现
根据算法设计描述,可以用一维数组 w[] 存储古董的重量。① 按重量排序。可以利用 C++ 中的排序函数 sort() 对古董按重量从小到大排序。要使用此函数,只需引入头文件:
#include<algorithm>。排序函数如下:
sort(w, w + n); // 按古董重量从小到大排序,参数分别为待排序数组的首地址和尾地址,默认为从小到大排序
② 根据贪心策略找最优解。首先用变量 ans 记录已装载的古董数量,tmp 代表已装载的古董重量,将两个变量都初始化为 0;然后在排序的基础上,依次检查每个古董的重量,使 tmp 加上该古董的重量,若其结果小于或等于载重 c,则令 ans++,否则退出。
double tmp = 0.0; // 已装载的古董重量 int ans = 0; // 已装载的古董数量 for (int i = 0; i < n; i++) { tmp += w[i]; if (tmp > c) break; ans++; }
4) 算法分析
时间复杂度:将古董按重量排序并调用 sort(),其在平均情况下的时间复杂度为 O(nlogn),求解过程中 for 语句的时间复杂度为 O(n),因此总时间复杂度为 O(nlogn)。空间复杂度:使用了 tmp、ans 等辅助变量,空间复杂度为 O(1)。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: