什么是贪心算法(新手必看)
贪心算法也叫贪婪算法,在对问题进行求解时,总是做出当前看来最好的选择。也就是说,不从整体上考虑是不是最优选择,所做出的选择仅是在某种意义上的局部最优解。
尽管贪心算法不能对所有问题都能得到整体最优解,但是它希望得到的解是整体最优的,对许多问题来说能产生整体最优解。在利用贪心算法求解问题时,所做的选择都是当前状态下的最优选择,并且所做的选择不会影响以前的状态,只与当前状态有关。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。考虑问题是否适合使用贪心算法,首先要看该问题是否满足贪心选择的最优子结构性质,若满足最优子结构性质,则可选择合适的贪心策略并进行求解。
做了贪心选择后,原问题可以简化成一个规模更小的类似子问题,而后面的每一步都是当前的最佳选择。这种选择依赖于已做出的选择,但不依赖于未做出的选择。运用贪心策略解决问题时并无回溯过程。
问题的最优子结构性质是该问题是否可用贪心算法求解的关键。所谓最优子结构性质,就是当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。原问题为 S={a1,a2,…,ai,…,an},通过贪心选择选出一个当前最优解 {ai} 之后,原问题就转换为求解子问题 S−{ai} 的最优解。
例如,对于背包问题,假设背包容量为 60,有 3 件物品,其重量和价值如下表所示:

表 1 物品的重量和价值
要选择合适的物品,物品可以拆分,使装入背包的总价值最大。
首先,计算每个物品的单位重量价值,分别为 3、5、2,按照单位重量价值对物品从大到小进行排序,如下表所示:

表 2 按单位重量价值排序后的物品重量和价值
然后依次选择物品装入背包,由于编号为 2 的物品重量小于背包的容量,即 30<60,因此将其装入背包,此时背包的剩余容量为 30,背包中物品的价值为 150,这样就是将原问题转换为规模更小的子问题求解。
检查编号为 1 的物品的重量是否能装入背包,由于 10<30,因此将其装入背包,此时背包的剩余容量为 20,背包中物品的价值为 180。
检查编号为 3 的物品是否能装入背包,由于 50>20,因此不能装入背包,只能装入其中的 2/5,相应的价值为 40,这样背包中物品的价值为 220,问题的解就是 (1.0, 1.0, 0.4),即第 1 个物品和第 2 个物品完全装入背包,第 3 个物品装入 40%。
1) 建立数学模型来描述问题。例如,对于背包问题,要求解的问题可形式化表示为:
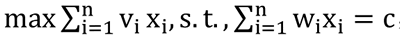 ,其中 xi 取值为 0 或 1。
,其中 xi 取值为 0 或 1。
2) 把求解的问题分成若干子问题。例如,对于背包问题,将第一个物品放入背包后,子问题就变为从剩下的物品选择装入背包,背包的容量变为减去第一个物品后的容量,即剩余容量。
3) 对每个子问题进行求解,得到子问题的局部最优解。例如,对于背包问题,选择装入背包的物品就是当前的最优选择,即当前单位重量价值最大的物物品。
4) 把子问题的局部最优解合成原来问题的一个解。
尽管贪心算法不能对所有问题都能得到整体最优解,但是它希望得到的解是整体最优的,对许多问题来说能产生整体最优解。在利用贪心算法求解问题时,所做的选择都是当前状态下的最优选择,并且所做的选择不会影响以前的状态,只与当前状态有关。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。考虑问题是否适合使用贪心算法,首先要看该问题是否满足贪心选择的最优子结构性质,若满足最优子结构性质,则可选择合适的贪心策略并进行求解。
贪心选择性质
贪心选择性质是指原问题的整体最优解可以通过一系列的局部最优选择得到。做了贪心选择后,原问题可以简化成一个规模更小的类似子问题,而后面的每一步都是当前的最佳选择。这种选择依赖于已做出的选择,但不依赖于未做出的选择。运用贪心策略解决问题时并无回溯过程。
问题的最优子结构性质是该问题是否可用贪心算法求解的关键。所谓最优子结构性质,就是当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。原问题为 S={a1,a2,…,ai,…,an},通过贪心选择选出一个当前最优解 {ai} 之后,原问题就转换为求解子问题 S−{ai} 的最优解。
例如,对于背包问题,假设背包容量为 60,有 3 件物品,其重量和价值如下表所示:

表 1 物品的重量和价值
要选择合适的物品,物品可以拆分,使装入背包的总价值最大。
首先,计算每个物品的单位重量价值,分别为 3、5、2,按照单位重量价值对物品从大到小进行排序,如下表所示:

表 2 按单位重量价值排序后的物品重量和价值
然后依次选择物品装入背包,由于编号为 2 的物品重量小于背包的容量,即 30<60,因此将其装入背包,此时背包的剩余容量为 30,背包中物品的价值为 150,这样就是将原问题转换为规模更小的子问题求解。
检查编号为 1 的物品的重量是否能装入背包,由于 10<30,因此将其装入背包,此时背包的剩余容量为 20,背包中物品的价值为 180。
检查编号为 3 的物品是否能装入背包,由于 50>20,因此不能装入背包,只能装入其中的 2/5,相应的价值为 40,这样背包中物品的价值为 220,问题的解就是 (1.0, 1.0, 0.4),即第 1 个物品和第 2 个物品完全装入背包,第 3 个物品装入 40%。
贪心算法的求解步骤
贪心算法的求解步骤如下:1) 建立数学模型来描述问题。例如,对于背包问题,要求解的问题可形式化表示为:
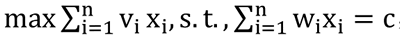
2) 把求解的问题分成若干子问题。例如,对于背包问题,将第一个物品放入背包后,子问题就变为从剩下的物品选择装入背包,背包的容量变为减去第一个物品后的容量,即剩余容量。
3) 对每个子问题进行求解,得到子问题的局部最优解。例如,对于背包问题,选择装入背包的物品就是当前的最优选择,即当前单位重量价值最大的物物品。
4) 把子问题的局部最优解合成原来问题的一个解。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: