01背包问题详解(C++实现,图文并茂)
所谓 01 背包问题,假设有 n 种物品和一个背包,每种物品 i 对应的价值都为 vi,重量都为 wi,背包容量为 W。每种物品只有一件,要么装入,要么不装入,不可拆分。如何选择物品装入背包,使背包所装入物品的价值之和最大?要求输出最优值(所装入物品的最大价值)和最优解(装入了哪些物品)。
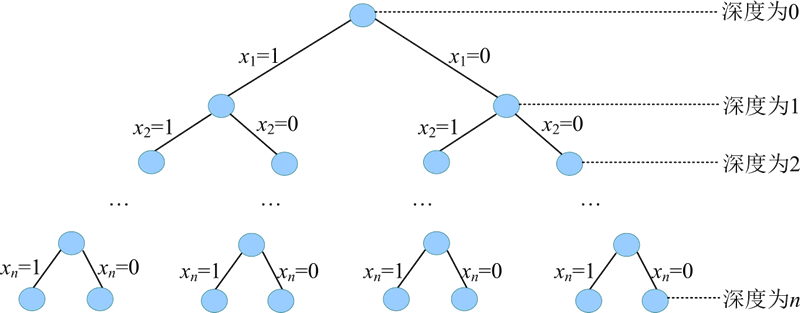
S 的所有子集都是问题的可能解,这些可能解组成解空间。在解空间中搜索总重量不超过背包容量且价值最大的物品集作为最优解。由问题的子集组成的解空间被称为“子集树”。
问题的解空间为 {x1,x2,…,xi,…,xn},其中 xi=0 或 1。
假设第 t+1 种物品到第 n 种物品都被装入背包,rp 表示第 t+1 种物品到第 n 种物品的总价值,cp 表示当前已装入背包的物品的价值,cp+rp 表示从根出发经过中间节点 z 的可行解上界。
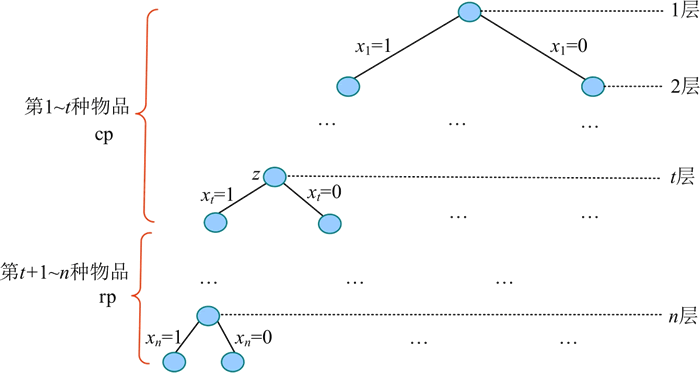
若可行解上界小于或等于当前搜索到的最优值 bestp,则说明从 z 继续向其子孙搜索不可能得到一个比当前更优的可行解,没有必要继续搜索;反之,继续向 z 的子孙搜索。限界条件是 cp+rp>bestp。

1) 初始化操作,sumw 和 sumv 分别表示所有物品的总重量和总价值。sumw=13,sumv=18,若 sumw≤W,则说明可以全部装入,最优值为 sumv。若 sumw>W,则不能全部装入,需要通过搜索求解。
初始化当前已装入背包的物品的重量 cw=0;当前已装入背包的物品的价值 cp=0;当前最优值 bestp=0。
2) 搜索第 1 层(t=1)。扩展节点 1,cw+w[1]=2<W,满足约束条件,扩展左分支,令 x1=1,cw=cw+w[1]=2,cp=cp+v[1]=6,生成节点 2。
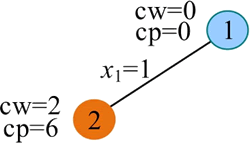
3) 扩展节点 2(t=2)。cw+w[2]=7<W,满足约束条件,扩展左分支,令 x2=1,cw=cw+w[2]=7,cp=cp+v[2]=9,生成节点 3。
4) 扩展节点 3(t=3)。cw+w[3]=11>W,超过了背包容量,第 3 种物品不能被装入。判断 Bound(t+1) 是否大于 bestp。Bound(4) 中剩余的物品只有第 4 个,rp=4,cp+rp=13,bestp=0,满足限界条件,扩展右分支。令 x3=0,生成节点 4。
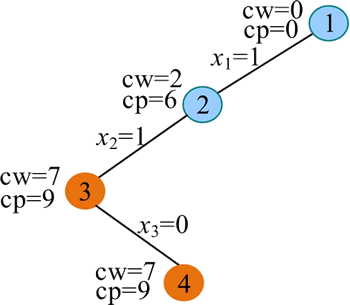
5) 扩展节点 4(t=4)。cw+w[4]=9<W,满足约束条件,扩展左分支,令 x4=1,cw=cw+w[4]=9,cp=cp+v[4]=13,生成节点 5。
6) 扩展节点 5(t=5)。t>n,找到当前最优解,用 bestx[] 保存当前最优解 {1,1,0,1},保存当前最优值 bestp=cp=13,如下图所示。
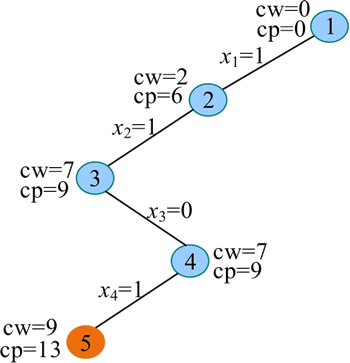
7) 回溯到节点 4(t=4),回溯时,cw=cw-w[4]=7,cp=cp-v[4]=9。怎么加上去的,就怎么减回去。
节点4 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,在 Bound(5) 中没有剩余物品,rp=0,cp+rp=9,bestp=13,因此不满足限界条件,不再扩展节点 4 的右分支。
向上回溯到节点 3,节点 3 的左、右孩子均已被考查过,继续向上回溯到节点 2。回溯时,cw=cw-w[2]=2,cp=cp-v[2]=6。
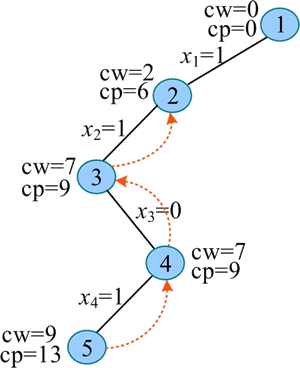
8) 扩展节点 2(t=2)。节点 2 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,Bound(3) 中剩余的物品为第 3、4 个,rp=9,cp+rp=15,bestp=13,因此满足限界条件,扩展右分支。令 x2=0,生成节点 6。
9) 扩展节点 6(t=3)。cw+w[3]=6<W,满足约束条件,扩展左分支,令 x3=1,cw=cw+w[3]=6,cp=cp+v[3]=11,生成节点 7。
10) 扩展节点 7(t=4)。cw+w[4]=8<W,满足约束条件,扩展左分支,令 x4=1,cw=cw+w[4]=8,cp=cp+v[4]=15,生成节点 8。

11) 扩展节点 8(t=5)。t>n,找到当前最优解,用 bestx[] 保存当前最优解 {1,0,1,1},保存当前最优值 bestp=cp=15。向上回溯到节点 7,回溯时,cw=cw-w[4]=6,cp=cp-v[4]=11。
12) 扩展节点 7(t=4)。节点 7 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,在 Bound(5) 中没有剩余物品,rp=0,cp+rp=11,bestp=15,因此不满足限界条件,不再扩展节点 7 的右分支。向上回溯到节点 6,回溯时,cw=cw-w[3]=2,cp=cp-v[3]=6。
13) 扩展节点 6(t=3)。节点 6 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,Bound(4) 中剩余的物品为第 4 个,rp=4,cp+rp=10,bestp=15,因此不满足限界条件,不再扩展节点 6 的右分支。
向上回溯到节点 2,节点 2 的左、右孩子均已被考查过,继续向上回溯到节点 1。回溯时,cw=cw-w[1]=0,cp=cp-v[1]=0。
14) 扩展节点 1(t=1)。节点 1 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,Bound(2) 中剩余的物品为第 2、3、4 个,rp=12,cp+rp=12,bestp=15,因此不满足限界条件,不再扩展节点 1 的右分支。所有节点搜索完毕,算法结束。
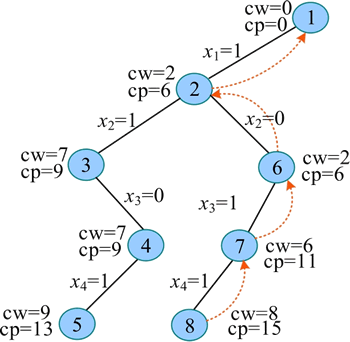
若 t>n,则表示已经到达叶子,记录最优值的最优解,返回;若满足约束条件,则搜索左子树,令 xt=1,表示装入第 t 种物品。cw+=w[t],表示当前已装入背包的物品的重量增加 w[t]。cp+=v[t],表示当前已装入背包的物品的价值增加 v[t]。深度优先搜索第 t+1 层。回归时向上回溯,把增加的值减去,cw-=w[t],cp-=v[t]。若满足限界条件,则搜索右子树,令 xt=0,当前已装入背包的物品的重量、价值均不改变,深度优先搜索第 t+1 层。
对左孩子需要判断约束函数,对右孩子需要判断限界函数,在最坏情况下有多少个左孩子和右孩子呢?规模为 n 的子集树在最坏情况下的状态如下图所示。
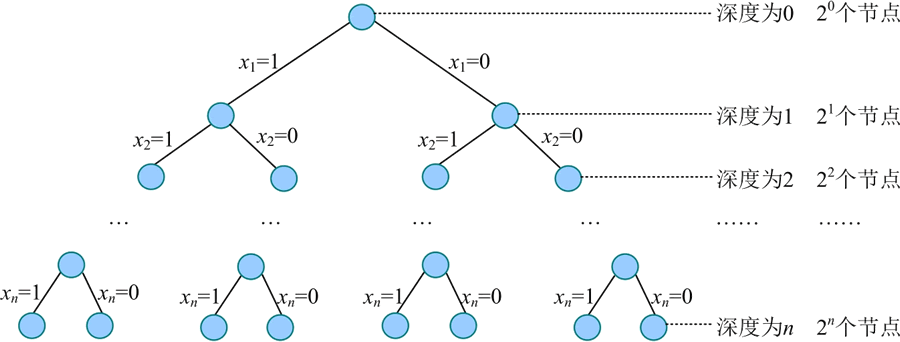
总节点数为 2^0+2^1+…+2^n=2^(n+1)-1,减去根再除以 2,就得到了左、右孩子数,左、右孩子数都为 (2^(n+1)-1-1)/2=2^n-1。
约束函数的时间复杂度为 O(1),限界函数的时间复杂度为 O(n)。因为在最坏情况下有 O(2^n) 个左孩子调用约束函数,有 O(2^n) 个右孩子调用限界函数,所以采用回溯法解决背包问题的时间复杂度为 O(1×2^n+n×2^n)=O(n×2^n)。
上界函数 Bound():当前价值 cp+ 背包剩余容量可容纳的剩余物品的最大价值 brp。为了更好地计算上界函数,首先将物品按照其单位重量价值(价值/重量)从大到小排序,然后按照排序后的顺序考查各种物品。
这里除了使用了最优解数组,还使用了一个结构体数组用于排序,空间复杂度为 O(n)。
01背包问题分析
从 n 种物品中选择一些物品,相当于从 n 种物品组成的集合 S 中找到一个子集,这个子集内所有物品的总重量不超过背包容量,并且这些物品的价值之和最大。S 的所有子集都是问题的可能解,这些可能解组成解空间。在解空间中搜索总重量不超过背包容量且价值最大的物品集作为最优解。由问题的子集组成的解空间被称为“子集树”。
1、定义问题的解空间
每种物品都有且只有两种状态:要么装入背包,要么不装入背包。用变量 xi 表示是否将第 i 种物品装入背包,“0”表示不装入背包,“1”表示装入背包。问题的解空间为 {x1,x2,…,xi,…,xn},其中 xi=0 或 1。
2、确定解空间的组织结构
问题的解空间描述了 2^n 种可能解,即由 n 个元素组成的集合的所有子集的数量。问题的解空间树为子集树,解空间树的深度为问题的规模 n。
3、搜索解空间
根据解空间的组织结构,对于任何一个中间节点 z(中间状态),从根到 z 的分支状态(是否装入背包)已确定,从 z 到其子孙的分支状态待确定。若 z 的层次是 t,则第 1 种物品到第 t-1 种物品的状态已确定,只需沿着 z 的分支扩展来确定第 t 种物品的状态。1) 约束条件
将第 i 种物品装入背包后总重量不能超过背包容量,约束条件为 cw+w[i]≤W。其中,cw 表示当前已装入背包的物品的重量,w[i] 表示第 i 种物品的重量,W 表示背包容量。2) 限界条件
已装入物品的价值高不一定就是最优的,因为还有剩余物品未确定实际状态。因为当前还不确定第 t+1 种物品到第 n 种物品的实际状态,所以只能使用估计值。假设第 t+1 种物品到第 n 种物品都被装入背包,rp 表示第 t+1 种物品到第 n 种物品的总价值,cp 表示当前已装入背包的物品的价值,cp+rp 表示从根出发经过中间节点 z 的可行解上界。

若可行解上界小于或等于当前搜索到的最优值 bestp,则说明从 z 继续向其子孙搜索不可能得到一个比当前更优的可行解,没有必要继续搜索;反之,继续向 z 的子孙搜索。限界条件是 cp+rp>bestp。
3) 搜索过程
从根开始进行深度优先搜索。在子集树中约定左分支上的值为 1,表示装入物品:- 若满足约束条件,则装入该物品,生成左孩子,继续向纵深节点扩展;否则剪掉左分支,沿着其右分支扩展,右分支上的值为 0,表示不装入物品。
- 若满足限界条件,则生成右孩子,继续向纵深节点扩展;否则剪掉右分支,向最近的祖先回溯,继续沿着其他分支搜索。
01背包问题完美图解
现有 4 种物品和 1 个背包,背包容量为 10(W=10),物品的重量和价值如下图所示。求在不超过背包容量的前提下把哪些物品装入背包,才能获得最大价值。
1) 初始化操作,sumw 和 sumv 分别表示所有物品的总重量和总价值。sumw=13,sumv=18,若 sumw≤W,则说明可以全部装入,最优值为 sumv。若 sumw>W,则不能全部装入,需要通过搜索求解。
初始化当前已装入背包的物品的重量 cw=0;当前已装入背包的物品的价值 cp=0;当前最优值 bestp=0。
2) 搜索第 1 层(t=1)。扩展节点 1,cw+w[1]=2<W,满足约束条件,扩展左分支,令 x1=1,cw=cw+w[1]=2,cp=cp+v[1]=6,生成节点 2。
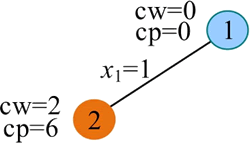
3) 扩展节点 2(t=2)。cw+w[2]=7<W,满足约束条件,扩展左分支,令 x2=1,cw=cw+w[2]=7,cp=cp+v[2]=9,生成节点 3。
4) 扩展节点 3(t=3)。cw+w[3]=11>W,超过了背包容量,第 3 种物品不能被装入。判断 Bound(t+1) 是否大于 bestp。Bound(4) 中剩余的物品只有第 4 个,rp=4,cp+rp=13,bestp=0,满足限界条件,扩展右分支。令 x3=0,生成节点 4。

5) 扩展节点 4(t=4)。cw+w[4]=9<W,满足约束条件,扩展左分支,令 x4=1,cw=cw+w[4]=9,cp=cp+v[4]=13,生成节点 5。
6) 扩展节点 5(t=5)。t>n,找到当前最优解,用 bestx[] 保存当前最优解 {1,1,0,1},保存当前最优值 bestp=cp=13,如下图所示。

7) 回溯到节点 4(t=4),回溯时,cw=cw-w[4]=7,cp=cp-v[4]=9。怎么加上去的,就怎么减回去。
节点4 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,在 Bound(5) 中没有剩余物品,rp=0,cp+rp=9,bestp=13,因此不满足限界条件,不再扩展节点 4 的右分支。
向上回溯到节点 3,节点 3 的左、右孩子均已被考查过,继续向上回溯到节点 2。回溯时,cw=cw-w[2]=2,cp=cp-v[2]=6。

8) 扩展节点 2(t=2)。节点 2 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,Bound(3) 中剩余的物品为第 3、4 个,rp=9,cp+rp=15,bestp=13,因此满足限界条件,扩展右分支。令 x2=0,生成节点 6。
9) 扩展节点 6(t=3)。cw+w[3]=6<W,满足约束条件,扩展左分支,令 x3=1,cw=cw+w[3]=6,cp=cp+v[3]=11,生成节点 7。
10) 扩展节点 7(t=4)。cw+w[4]=8<W,满足约束条件,扩展左分支,令 x4=1,cw=cw+w[4]=8,cp=cp+v[4]=15,生成节点 8。

11) 扩展节点 8(t=5)。t>n,找到当前最优解,用 bestx[] 保存当前最优解 {1,0,1,1},保存当前最优值 bestp=cp=15。向上回溯到节点 7,回溯时,cw=cw-w[4]=6,cp=cp-v[4]=11。
12) 扩展节点 7(t=4)。节点 7 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,在 Bound(5) 中没有剩余物品,rp=0,cp+rp=11,bestp=15,因此不满足限界条件,不再扩展节点 7 的右分支。向上回溯到节点 6,回溯时,cw=cw-w[3]=2,cp=cp-v[3]=6。
13) 扩展节点 6(t=3)。节点 6 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,Bound(4) 中剩余的物品为第 4 个,rp=4,cp+rp=10,bestp=15,因此不满足限界条件,不再扩展节点 6 的右分支。
向上回溯到节点 2,节点 2 的左、右孩子均已被考查过,继续向上回溯到节点 1。回溯时,cw=cw-w[1]=0,cp=cp-v[1]=0。
14) 扩展节点 1(t=1)。节点 1 的右子树还未生成,考查 Bound(t+1) 是否大于 bestp,Bound(2) 中剩余的物品为第 2、3、4 个,rp=12,cp+rp=12,bestp=15,因此不满足限界条件,不再扩展节点 1 的右分支。所有节点搜索完毕,算法结束。

01背包问题算法实现
1) 计算上界
计算上界指计算已装入物品的价值 cp 和剩余物品的总价值 rp。因为不确定要装入哪些剩余物品,所以假设都被装入,即按最大值来计算(剩余物品的总价值),得到的值是可装入物品的价值的上界。2) 按约束条件和限界条件搜索求解
t 表示当前扩展节点的层次,cw 表示当前已装入背包的物品的重量,cp 表示当前已装入背包的物品的价值。若 t>n,则表示已经到达叶子,记录最优值的最优解,返回;若满足约束条件,则搜索左子树,令 xt=1,表示装入第 t 种物品。cw+=w[t],表示当前已装入背包的物品的重量增加 w[t]。cp+=v[t],表示当前已装入背包的物品的价值增加 v[t]。深度优先搜索第 t+1 层。回归时向上回溯,把增加的值减去,cw-=w[t],cp-=v[t]。若满足限界条件,则搜索右子树,令 xt=0,当前已装入背包的物品的重量、价值均不改变,深度优先搜索第 t+1 层。
void Backtrack(int t) { // t 表示当前扩展节点在第 t 层
if(t > n) // 已经到达叶子
{
for(j = 1; j <= n; j++) {
bestx[j] = x[j];
}
bestp = cp; // 保存当前最优解
return;
}
if(cw + w[t] <= W) { // 若满足约束条件,则搜索左子树
x[t] = 1;
cw += w[t];
cp += v[t];
Backtrack(t + 1);
cw -= w[t];
cp -= v[t];
}
if(Bound(t + 1) > bestp) { // 若满足限界条件,则搜索右子树
x[t] = 0;
Backtrack(t + 1);
}
}
01背包问题算法分析
1) 时间复杂度
回溯法的运行时间取决于在搜索过程中生成的节点数。限界函数可以大大减少所生成的节点数,避免无效搜索,加快搜索速度。对左孩子需要判断约束函数,对右孩子需要判断限界函数,在最坏情况下有多少个左孩子和右孩子呢?规模为 n 的子集树在最坏情况下的状态如下图所示。

总节点数为 2^0+2^1+…+2^n=2^(n+1)-1,减去根再除以 2,就得到了左、右孩子数,左、右孩子数都为 (2^(n+1)-1-1)/2=2^n-1。
约束函数的时间复杂度为 O(1),限界函数的时间复杂度为 O(n)。因为在最坏情况下有 O(2^n) 个左孩子调用约束函数,有 O(2^n) 个右孩子调用限界函数,所以采用回溯法解决背包问题的时间复杂度为 O(1×2^n+n×2^n)=O(n×2^n)。
2) 空间复杂度
使用数组 bestx[] 保存最优解,空间复杂度为 O(n)。【算法优化拓展】
在上面的程序中,上界函数是当前已装入背包的物品的价值 cp 加剩余物品的总价值 rp,这个估值过高,因为剩余物品很可能是无法被全部装入的。可以缩小上界,加快剪枝速度,提高搜索效率。上界函数 Bound():当前价值 cp+ 背包剩余容量可容纳的剩余物品的最大价值 brp。为了更好地计算上界函数,首先将物品按照其单位重量价值(价值/重量)从大到小排序,然后按照排序后的顺序考查各种物品。
double Bound(int i) { // 计算上界(将剩余物品装满背包剩余容量获得的最大价值)
// 剩余的为第 i~n 种物品
double cleft = W - cw; // 背包剩余容量
double brp = 0.0;
while(i <= n && w[i] <= cleft) {
cleft -= w[i];
brp += v[i];
i++;
}
if(i <= n) // 采用切割方式装满背包,这里是在求上界,求解时不允许切割
brp += 1.0 * v[i] / w[i] * cleft;
return cp + brp;
}
约束函数的时间复杂度为 O(1),限界函数的时间复杂度为 O(n)。在最坏情况下有 O(2^n) 个左孩子需要调用约束函数,有 O(2^n)个右孩子需要调用限界函数,回溯算法的时间复杂度为 O(n2^n)。排序函数的时间复杂度为 O(logn)。这里考虑了最坏情况,实际上经过上界函数优化后,剪枝速度很快,根本不需要生成所有节点。这里除了使用了最优解数组,还使用了一个结构体数组用于排序,空间复杂度为 O(n)。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: