Python绘制勾股树详解(附带源码)
勾股树是根据勾股定理绘制的可以无限重复的图形,重复多次之后呈现为树状。
勾股树最早是由古希腊数学家毕达哥拉斯绘制,因此又称之为毕达哥拉斯树。这种图形在数学上称为分形图,它们中的一个部分与其整体或者其他部分都十分相似,分形图内任何一个相对独立的部分,在一定程度上都是整体的再现和缩影。这就是分形图的自相似特性。
勾股定理的定义:在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。用数学语言表达为 a^2+b^2=c^2,用图形表达如下图所示。
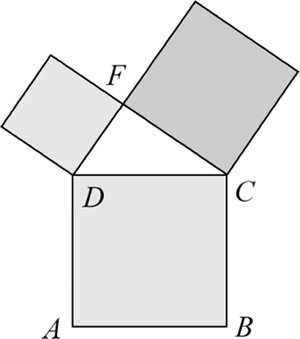
图 1 勾股定理图
以图 1 中的勾股定理图为基础,让两个较小的正方形按勾股定理继续“生长”,又能画出新一代的勾股定理图,如此一直画下去,最终得到一棵完全由勾股定理图组成的树状图形。
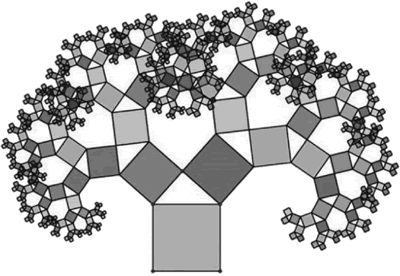
图 2 勾股树
1) 先画出图 1 所示的勾股定理图形作为基本图形,将这一过程封装为一个绘图函数,以便进行递归调用。
2) 在绘制两个小正方形之前,分别以直角三角形两条直角边作为下一代勾股定理图形中直角三角形的斜边,以递归方式调用绘制函数画出下一代的基本图形。
3) 重复执行前两步,最终可绘制出一棵勾股树的分形图。由于是递归调用,需要递归的终止条件,此处设置某一代勾股定理图的直角三角形的斜边小于某个数值时就结束递归。
前一排的长度递归相当于“满二叉树”的先序遍历,从根出发先左子树后右子树,每一棵子树都按这种“先根后左右”的顺序遍历。
【实例 1】 绘制分形树。
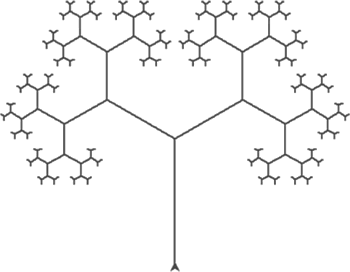
图 3 分形树
在以上代码中,长度以等比数列递减,公比为 1/1.6;也可以改成等差数列形式。此方式缺点是:树的层数不能直接控制,需要用初始长度、递减公式和退出条件计算得出。
【实例 2】 绘制勾股树。
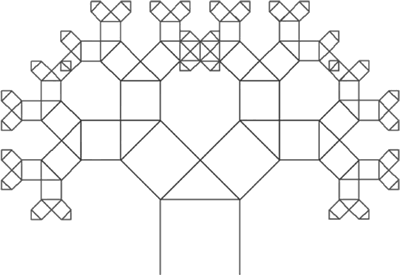
图 4 勾股树
勾股树最早是由古希腊数学家毕达哥拉斯绘制,因此又称之为毕达哥拉斯树。这种图形在数学上称为分形图,它们中的一个部分与其整体或者其他部分都十分相似,分形图内任何一个相对独立的部分,在一定程度上都是整体的再现和缩影。这就是分形图的自相似特性。
勾股定理的定义:在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。用数学语言表达为 a^2+b^2=c^2,用图形表达如下图所示。

图 1 勾股定理图
以图 1 中的勾股定理图为基础,让两个较小的正方形按勾股定理继续“生长”,又能画出新一代的勾股定理图,如此一直画下去,最终得到一棵完全由勾股定理图组成的树状图形。

图 2 勾股树
算法分析
利用分形图的自相似特性,先构造出分形图的基本图形,再不断地对基本图形进行复制,就能绘制出分形图。针对勾股树分形图,其绘制步骤如下:1) 先画出图 1 所示的勾股定理图形作为基本图形,将这一过程封装为一个绘图函数,以便进行递归调用。
2) 在绘制两个小正方形之前,分别以直角三角形两条直角边作为下一代勾股定理图形中直角三角形的斜边,以递归方式调用绘制函数画出下一代的基本图形。
3) 重复执行前两步,最终可绘制出一棵勾股树的分形图。由于是递归调用,需要递归的终止条件,此处设置某一代勾股定理图的直角三角形的斜边小于某个数值时就结束递归。
绘制分形树和勾股树
接下来通过 Python 分别实现分形树与勾股树的绘制。1) 分形树
分形树是分形几何中的一小种类型,一棵分形树相当于一棵“满二叉树”。通常都用递归来实现,递归条件通常分两排:- 一排是用长度递减,直到长度不满足某个条件时退出;
- 另一排则是按层数递归,相当于“满二叉树”的层序遍历。
前一排的长度递归相当于“满二叉树”的先序遍历,从根出发先左子树后右子树,每一棵子树都按这种“先根后左右”的顺序遍历。
【实例 1】 绘制分形树。
import turtle
def bintree(size):
angle = 60 #分叉的角度
if size>5: #长度退出条件
turtle.forward(size)
turtle.left(angle)
bintree(size/1.6)
turtle.right(angle * 2)
bintree(size/1.6)
turtle.left(angle)
turtle.backward(size)
def main():
turtle.speed(0)
turtle.hideturtle()
turtle.penup()
turtle.left(90)
turtle.backward(100)
turtle.showturtle()
turtle.pendown()
turtle.pensize(2)
turtle.color('green')
bintree(150)
turtle.done()
if__name__ == '__main__':
main()
运行程序,效果如下图所示:
图 3 分形树
在以上代码中,长度以等比数列递减,公比为 1/1.6;也可以改成等差数列形式。此方式缺点是:树的层数不能直接控制,需要用初始长度、递减公式和退出条件计算得出。
2) 勾股树
勾股树,其实就是分形树的一种,只是不像上例一样简单地画2个分叉,而是画直角三角形加上各边上的正方形,就像平面几何中勾股定理证明时画的示意图。【实例 2】 绘制勾股树。
from turtle import *
def Square(self,length):
for_in range(5):
self.forward(length)
self.right(90)
def Triangle(self,length):
self.left(45)
self.forward(length/2 * * 0.5)
self.right(90)
self.forward(length/2 * * 0.5)
self.right(135)
self.forward(length)
def Move2Right(self,length):
self.back(length)
self.right(45)
self.forward(length/2 * * 0.5)
self.right(90)
def Recursive(n,tracer,length):
if n<1:return
tracers = []
for left in tracer:
if n<3:left.pencolor('green')
else:left.pencolor('brown')
Square(left,length)
Triangle(left,length)
right = left.clone()
left.right(45)
Move2Right(right,length)
tracers.append(left)
tracers.append(right)
Recursive(n-1,tracers,length/2 * * 0.5)
def Setup(self,length,speed):
self.hideturtle()
self.speed(speed)
self.penup()
self.goto(-length * 0.5,-length * 1.8)
self.seth(90)
self.pensize(2)
self.pendown()
def main(level,length,speed = -1):
#level:树的层数
#length:最底层正方形的边长
#speed:1~10,画笔速度递增; = 0时速度最快; = -1时关闭画笔踪迹
setup(800,600)
title('Fractal Tree')
if speed == -1:tracer(0)
else:tracer(1)
t = Turtle()
Setup(t,length,speed)
from time import sleep
sleep(2)
Recursive(level,list([t]),length)
done()
bye()
if__name__ == '__main__':
main(6,150,10)
运行程序,效果如下图所示:
图 4 勾股树
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: