什么是损失函数,PyTorch常见的损失函数有哪些(非常详细)
损失函数是统计学和机器学习等领域的基础概念,它将随机事件或与其相关的随机变量的取值映射为非负实数,用来表示该随机事件的风险或损失。
本节介绍损失函数,以及 PyTorch 中常用的几种损失函数。
受到应用场景、数据集和待求解问题等因素的制约,现有监督学习算法使用的损失函数的种类和数量较多,而且每个损失函数都有各自的特征,因此从众多损失函数中选择适合求解问题最优模型的损失函数是相当困难的。
在监督学习中,损失函数表示单个样本真实值与模型预测值之间的偏差,其值通常用于衡量模型的性能。现有的监督学习算法不仅使用了损失函数,而且求解不同应用场景的算法会使用不同的损失函数。
研究表明,即使在相同场景下,不同的损失函数度量同一样本的性能时也存在差异。可见,损失函数的选用是否合理直接决定着监督学习算法预测性能的优劣。
在实际问题中,损失函数的选取有许多约束,如机器学习算法的选择、是否有离群点、梯度下降的复杂性、求导的难易程度以及预测值的置信度等。
目前,没有一种损失函数能完美处理所有类型的数据。在同等条件下,模型选取的损失函数越能扩大样本的类间距离、减小样本的类内距离,模型预测的精确度就越高。
实践表明,在同一模型中,与求解问题数据相匹配的损失函数往往对提升模型的预测能力起着关键作用。因此,如果能正确理解各种损失函数的特性,分析它们适用的应用场景,针对特定问题选取合适的损失函数,就可以进一步提高模型的预测精度。
损失函数的标准数学形式不仅种类多,而且每类损失函数又在其标准形式的基础上演化出了许多形式。0-1 损失函数是最简单的损失函数,在其基础上加入参数控制损失范围,形成感知机损失函数;加入安全边界,演化为铰链损失函数。可见,损失函数的发展不是孤立的,而是随着应用研究的发展进行变革的。在 PyTorch 中,损失函数通过 torch.nn 包实现调用。
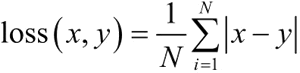
模型调用方法如下:
示例代码如下:
两个输入类型必须一致,reduction 是损失函数一个参数,有三个值:
上面的例子不同参数分别返回 tensor([3., 3., 3.,3.])、tensor(3.) 和 tensor(12.)。
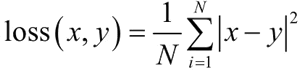
模型调用方法如下:
示例代码如下:
默认情况下,这两个参数都为 True。
首先介绍一下交叉熵的概念,它用来判定实际输出与期望输出的接近程度,例如分类训练的时候,如果一个样本属于第 K 类,那么这个类别所对应的输出节点的输出值应该为 1,而其他节点的输出值都为 0,即 [0,0,1,0,…,0,0],也就是样本的标签,它是神经网络最期望的输出。也就是说,用它来衡量网络的输出与标签的差异,利用这种差异通过反向传播来更新网络参数。
交叉熵主要刻画的是实际输出概率与期望输出概率的距离,也就是交叉熵的值越小,两个概率分布就越接近,假设概率分布 p 为期望输出,概率分布 q 为实际输出,计算公式如下:
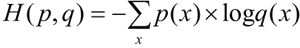
模型调用方法如下:
示例代码如下:
注意,这两个向量都是有梯度的,计算公式如下:
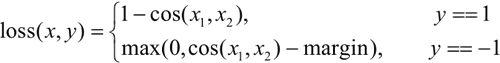
其中,margin 可以取 [-1,1],但是建议取 0~0.5。
模型调用方法如下:
本节介绍损失函数,以及 PyTorch 中常用的几种损失函数。
损失函数及其选取
监督学习中的损失函数常用来评估样本的真实值和模型预测值之间的不一致程度,一般用于模型的参数估计。受到应用场景、数据集和待求解问题等因素的制约,现有监督学习算法使用的损失函数的种类和数量较多,而且每个损失函数都有各自的特征,因此从众多损失函数中选择适合求解问题最优模型的损失函数是相当困难的。
在监督学习中,损失函数表示单个样本真实值与模型预测值之间的偏差,其值通常用于衡量模型的性能。现有的监督学习算法不仅使用了损失函数,而且求解不同应用场景的算法会使用不同的损失函数。
研究表明,即使在相同场景下,不同的损失函数度量同一样本的性能时也存在差异。可见,损失函数的选用是否合理直接决定着监督学习算法预测性能的优劣。
在实际问题中,损失函数的选取有许多约束,如机器学习算法的选择、是否有离群点、梯度下降的复杂性、求导的难易程度以及预测值的置信度等。
目前,没有一种损失函数能完美处理所有类型的数据。在同等条件下,模型选取的损失函数越能扩大样本的类间距离、减小样本的类内距离,模型预测的精确度就越高。
实践表明,在同一模型中,与求解问题数据相匹配的损失函数往往对提升模型的预测能力起着关键作用。因此,如果能正确理解各种损失函数的特性,分析它们适用的应用场景,针对特定问题选取合适的损失函数,就可以进一步提高模型的预测精度。
损失函数的标准数学形式不仅种类多,而且每类损失函数又在其标准形式的基础上演化出了许多形式。0-1 损失函数是最简单的损失函数,在其基础上加入参数控制损失范围,形成感知机损失函数;加入安全边界,演化为铰链损失函数。可见,损失函数的发展不是孤立的,而是随着应用研究的发展进行变革的。在 PyTorch 中,损失函数通过 torch.nn 包实现调用。
L1范数损失函数
L1 范数损失即 L1Loss,计算方法比较简单,原理就是取预测值和真实值的绝对误差的平均数,计算模型预测输出 output 和目标 target 之差的绝对值,可选择返回同维度的张量或者标量,计算公式如下: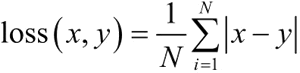
模型调用方法如下:
torch.nn.L1Loss(size_average=None,reduce=None,reduction='mean')代码说明:
- size_average:当 reduce=True 时有效。为 True 时,返回的 loss 为平均值;为 False 时,返回的 loss 为各样本的 loss 值之和。
- reduce:返回值是否为标量,默认为 True。
示例代码如下:
import torch # 导入PyTorch库 # 定义一个L1损失函数,计算输入和目标之间的平均绝对误差 loss = torch.nn.L1Loss(reduction='mean') input = torch.tensor([1.0, 2.0, 3.0, 4.0]) # 创建一个张量作为输入数据 target = torch.tensor([4.0, 5.0, 6.0, 7.0]) # 创建一个张量作为目标数据 output = loss(input, target) # 计算输入和目标之间的平均绝对误差 print(output) # 打印输出结果输出结果如下:
tensor(3.)
两个输入类型必须一致,reduction 是损失函数一个参数,有三个值:
- 'none' 返回的是一个向量 (batch_size);
- 'sum' 返回的是和;
- 'mean' 返回的是均值。
上面的例子不同参数分别返回 tensor([3., 3., 3.,3.])、tensor(3.) 和 tensor(12.)。
均方误差损失函数
均方误差损失即 MSELoss,计算公式是预测值和真实值之间的平方和的平均数,计算模型预测输出 output 和目标 target 之差的平方,可选返回同维度的张量或者标量,计算公式如下: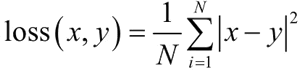
模型调用方法如下:
torch.nn.MSELoss(reduce=True,size_average=True,reduction='mean')代码说明:
- reduce:返回值是否为标量,默认为 True;
- size_average:当 reduce=True 时有效。为 True 时,返回的 loss 为平均值;为 False 时,返回的 loss 为各样本的 loss 值之和。
示例代码如下:
import torch # 导入PyTorch库 # 定义一个L1损失函数,计算输入和目标之间的平均绝对误差 loss = torch.nn.L1Loss(reduction='mean') input = torch.tensor([1.0, 2.0, 3.0, 4.0]) # 创建一个张量作为输入数据 target = torch.tensor([4.0, 5.0, 6.0, 7.0]) # 创建一个张量作为目标数据 # 定义一个均方误差损失函数,计算输入和目标之间的平均平方误差 loss_fn = torch.nn.MSELoss(reduction='mean') loss = loss_fn(input, target) # 计算输入和目标之间的平均平方误差 print(loss) # 打印输出结果输出结果如下:
tensor(9.)
这里注意一下两个入参:- reduce=False,返回向量形式的 loss;reduce=True,返回标量形式的 loss。
- size_average=True,返回 loss.mean();size_average=False,则返回 loss.sum()。
默认情况下,这两个参数都为 True。
交叉熵损失函数
交叉熵损失(Cross Entropy Loss)函数结合了 nn.LogSoftmax() 和 nn.NLLLoss() 两个函数,在做分类训练的时候非常有用。首先介绍一下交叉熵的概念,它用来判定实际输出与期望输出的接近程度,例如分类训练的时候,如果一个样本属于第 K 类,那么这个类别所对应的输出节点的输出值应该为 1,而其他节点的输出值都为 0,即 [0,0,1,0,…,0,0],也就是样本的标签,它是神经网络最期望的输出。也就是说,用它来衡量网络的输出与标签的差异,利用这种差异通过反向传播来更新网络参数。
交叉熵主要刻画的是实际输出概率与期望输出概率的距离,也就是交叉熵的值越小,两个概率分布就越接近,假设概率分布 p 为期望输出,概率分布 q 为实际输出,计算公式如下:
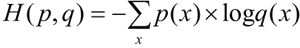
模型调用方法如下:
torch.nn.CrossEntropyLoss(weight=None,size_average=None,ignore_index=-100,reduce=None,reduction=’mean’)代码说明:
- weight(tensor):n 个元素的一维张量,分别代表 n 类权重,如果训练样本很不均衡的话,则非常有用,默认值为 None。
- size_average:当 reduce=True 时有效。为 True 时,返回的 loss 为平均值;为 False 时,返回的 loss 为各样本的 loss 值之和。
- ignore_index:忽略某一类别,不计算其 loss,并且在采用 size_average 时,不会计算那一类的 loss 值。
- reduce:返回值是否为标量,默认为 True。
示例代码如下:
import torch # 导入PyTorch库 entroy = torch.nn.CrossEntropyLoss() # 定义一个交叉熵损失函数 # 创建一个张量作为输入数据 input = torch.Tensor([[-0.1181, -0.3682, -0.2209]]) target = torch.tensor([0]) # 创建一个张量作为目标数据 output = entroy(input, target) # 计算输入和目标之间的交叉熵损失 print(output) # 打印输出结果输出结果如下:
tensor(0.9862)
余弦相似度损失
余弦相似度损失(Cosine Similarity Loss)通常用于度量两个向量的相似性,可以通过最大化这个相似度来进行优化。注意,这两个向量都是有梯度的,计算公式如下:
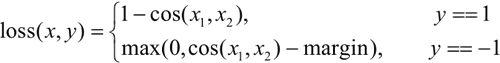
其中,margin 可以取 [-1,1],但是建议取 0~0.5。
模型调用方法如下:
torch.nn.CosineEmbeddingLoss(margin=0.0, reduction='mean')示例代码如下:
import torch # 导入PyTorch库 a = torch.tensor([1.0, 2.0, 3.0, 4.0]) # 创建一个张量作为输入数据 b = torch.tensor([4.1, 6.1, 7.1, 8.1]) # 创建一个张量作为目标数据 # 计算两个张量的余弦相似度,dim=0表示按列计算 similarity = torch.cosine_similarity(a, b, dim=0) loss = 1 - similarity # 计算损失值,即1减去相似度 print(loss) # 打印输出结果输出结果如下:
tensor(0.0199)
其他损失函数
除了前面介绍的 4 类损失函数外,PyTorch 2.2 中还有 16 类损失函数,如下表所示,具体用法和参数含义可以参考 PyTorch 官方文档的介绍。| 编号 | 损失函数 | 函数说明 |
|---|---|---|
| 1 | nn.CTCLoss | 连接时序分类损失 |
| 2 | nn.NLLLoss | 负对数似然损失 |
| 3 | nn.PoissonNLLLoss | 泊松负对数似然损失 |
| 4 | nn.GaussianNLLLoss | 高斯负对数似然损失 |
| 5 | nn.KLDivLoss | KL 散度损失 |
| 6 | nn.BCELoss | 二进制交叉熵损失 |
| 7 | nn.BCEWithLogitsLoss | 逻辑二进制交叉熵损失 |
| 8 | nn.MarginRankingLoss | 间隔排序损失 |
| 9 | nn.HingeEmbeddingLoss | 铰链嵌入损失 |
| 10 | nn.MultiLabelMarginLoss | 多标签分类损失 |
| 11 | nn.SoftMarginLoss | 两分类逻辑损失 |
| 12 | nn.MultiLabelSoftMarginLoss | 多标签逻辑损失 |
| 13 | nn.SmoothL1Loss | 平滑 L1 损失 |
| 14 | nn.MultiMarginLoss | 多类别分类损失 |
| 15 | nn.TripletMarginLoss | 三元组损失 |
| 16 | nn.TripletMarginWithDistanceLoss | 距离三元组损失 |
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: