顺序表是什么,顺序表的基本操作详解(Java实现)
要想在计算机上表示线性表,必须先将其逻辑结构转换为存储结构存放在计算机中。线性表的存储结构主要有两种:顺序存储和链式存储。
本节讨论线性表的顺序存储及其基本操作。
顺序表的特征是,逻辑上相邻的元素,在物理上也是相邻的。
假设线性表有 n 个元素,每个元素占用 m 个存储单元,若第一个元素的存储位置为 LOC(a1),第 i 个元素的存储位置为 LOC(ai),第 i+1 个元素的存储位置为 LOC(ai+1),则线性表的第 i+1 个元素的存储位置与第 i 个元素的存储位置满足以下关系:
线性表的第 i 个元素 ai 的存储位置与第一个元素 a1 的存储位置满足以下关系:
线性表的顺序存储结构是一种随机存取的存储结构。只要知道其中一个元素的存储地址,就可以得到线性表中任何一个元素的存储地址。
线性表的顺序存储结构如下图所示:
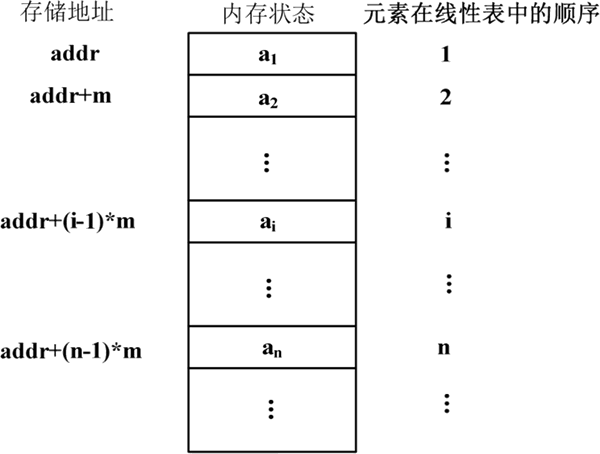
图 1 线性表的顺序存储结构
由于在 Java 语言中,数组具有存储地址连续、随机存取的特点,因此可采用数组来存储顺序表中的元素。顺序表的存储结构描述如下:
按序号查找就是查找顺序表 L 中的第 i 个元素,若找到该元素的值,则返回该元素的值。
按内容查找:
要在顺序表中的第 i 个位置插入元素 e,首先需要将表中位置为 n、n-1、…、i 的元素依次后移一个位置,将第 i 个位置空出,然后在该位置插入新元素 e。
当 i=n+1 时,在顺序表的末尾插入元素,无须移动元素,直接将 e 插入表的末尾即可。
例如,要在顺序表 {3,15,49,20,23,44,18,36} 的第 5 个元素之前插入一个元素 22,需要将 36、18、44、23 依次向后移动一个位置,然后在第 5 个位置插入元素 22,顺序表就变成了 {3,15,49,20,22,23,44,18,36},如下图所示。
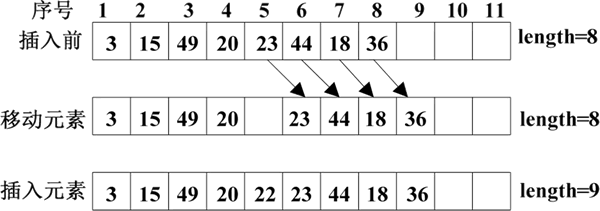
图 2 在顺序表中插入元素22的过程
为了删除顺序表中的第 i 个元素,需要将第 i+1 个位置之后的元素依次向前移动一个位置,即先将第 i+1 个元素移动到第 i 个位置,再将第 i+2 个元素移动到第 i+1 个位置,以此类推,直到将最后一个元素移动到倒数第二个位置。最后将顺序表的长度减 1。
例如,要删除顺序表 {3,15,49,20,22,23,44,18,36} 的第 4 个元素,需要将序号为 5、6、7、8、9 的元素依次向前移动一个位置,这样就删除了第 4 个元素,最后将表长减 1,如下图所示。
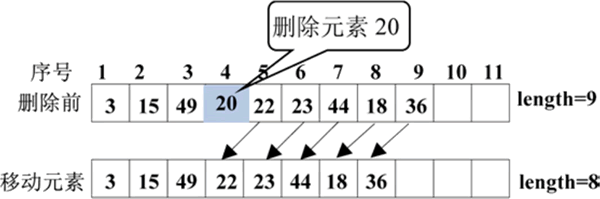
图 3 在顺序表中删除元素20的过程
在删除元素时,首先要判断顺序表中是否有元素,其次要判断要删除的元素的序号是否合法。删除成功后,将顺序表的长度减 1。
在以上顺序表的基本操作算法中,除了按内容查找、插入和删除外,算法的时间复杂度都为 O(1)。
在按内容查找的算法中,若要查找的元素在第一个位置,则需要比较一次;若要查找的元素在最后一个位置,则需要比较 n 次(n 为线性表的长度)。设 pi 为在第 i 个位置找到与 e 相等的元素的概率,假设在任何位置找到元素的概率相等,即 pi=1/n,则查找过程中需要比较的平均次数为:
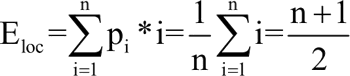
因此,按内容查找的平均时间复杂度为 O(n)。
在顺序表的插入算法中,时间的耗费主要集中在移动元素上。若要插入的元素在第一个位置,则需要移动元素的次数为 n;若要插入的元素在最后一个位置,则需要移动元素的次数为 1;若插入位置在最后一个元素之后,即第 n+1 个位置,则需要移动元素的次数为 0。设 pi 为在第 i 个位置插入元素的概率,假设在任何位置找到元素的概率相等,即 pi=1/(n+1),则顺序表的插入操作需要移动元素的平均次数为:
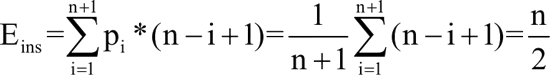
因此,插入操作的平均时间复杂度为 O(n)。
在顺序表的删除算法中,时间的耗费同样在移动元素上。若要删除的元素是第一个元素,则需要移动元素的次数为 n-1;若要删除的元素是最后一个元素,则需要移动元素的次数为 0。设 pi 表示删除第 i 个位置的元素的概率,假设在任何位置找到元素的概率相等,即 pi=1/n,则顺序表的删除操作需要移动元素的平均次数为:
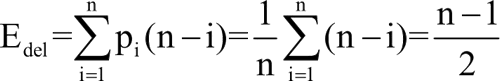
因此,删除操作的平均时间复杂度为 O(n)。
本节讨论线性表的顺序存储及其基本操作。
线性表的顺序存储
线性表的顺序存储指的是将线性表中的各个元素依次存放在一组地址连续的存储单元中,用这种方法存储的线性表称为顺序表。顺序表的特征是,逻辑上相邻的元素,在物理上也是相邻的。
假设线性表有 n 个元素,每个元素占用 m 个存储单元,若第一个元素的存储位置为 LOC(a1),第 i 个元素的存储位置为 LOC(ai),第 i+1 个元素的存储位置为 LOC(ai+1),则线性表的第 i+1 个元素的存储位置与第 i 个元素的存储位置满足以下关系:
LOC(ai+1)=LOC(ai)+m
线性表的第 i 个元素 ai 的存储位置与第一个元素 a1 的存储位置满足以下关系:
LOC(ai)=LOC(a1)+(i-1)*m
其中,第一个元素的位置 LOC(a1) 称为起始地址或基地址。线性表的顺序存储结构是一种随机存取的存储结构。只要知道其中一个元素的存储地址,就可以得到线性表中任何一个元素的存储地址。
线性表的顺序存储结构如下图所示:

图 1 线性表的顺序存储结构
由于在 Java 语言中,数组具有存储地址连续、随机存取的特点,因此可采用数组来存储顺序表中的元素。顺序表的存储结构描述如下:
public class SeqList<T> {
static final int LISTSIZE = 100;
private int length;
T list[];
SeqList() {
list = (T[]) new Object[LISTSIZE];
length = 0;
}
}
其中,SeqList 是类名,list 用于存储顺序表中的数据元素,length 表示顺序表当前的数据元素个数。顺序表的构造函数 SeqList() 包含顺序表的成员变量定义及初始化。顺序表的基本操作
1) 顺序表的初始化
顺序表的初始化可通过构造函数来实现:
SeqList() {
list = (T[]) new Object[LISTSIZE];
length = 0;
}
2) 判断顺序表是否为空
public boolean ListEmpty() //判断线性表是否为空
{
if (length == 0)
return true;
else
return false;
}
3) 查找操作
查找操作分为两种:按序号查找和按内容查找。按序号查找就是查找顺序表 L 中的第 i 个元素,若找到该元素的值,则返回该元素的值。
public T GetElem(int i) //取线性表中某一位置上的元素的值
{
if (i >= 1 && i <= length)
return list[i - 1];
else
throw new IllegalArgumentException("i 超出了线性表的有效范围!");
}
按内容查找:
public int LocateElem(T x)
{
int i;
for (i = 0; i < length; i++)
{
if (list[i] == x)
return i + 1;
}
return -1;
}
4) 插入操作
插入操作就是在顺序表 L 中的第 i 个位置插入新元素 e,顺序表的长度也由 n 变成 n+1。要在顺序表中的第 i 个位置插入元素 e,首先需要将表中位置为 n、n-1、…、i 的元素依次后移一个位置,将第 i 个位置空出,然后在该位置插入新元素 e。
当 i=n+1 时,在顺序表的末尾插入元素,无须移动元素,直接将 e 插入表的末尾即可。
例如,要在顺序表 {3,15,49,20,23,44,18,36} 的第 5 个元素之前插入一个元素 22,需要将 36、18、44、23 依次向后移动一个位置,然后在第 5 个位置插入元素 22,顺序表就变成了 {3,15,49,20,22,23,44,18,36},如下图所示。

图 2 在顺序表中插入元素22的过程
public boolean InsertList(int i, T e)
{
if (length >= LISTSIZE) {
System.out.println("顺序表空间已满!");
return false;
}
if (i < 1 || i > length + 1)
{
System.out.println("插入位置不合法");
return false;
}
else {
for (int j = length; j > i - 1; j = j - 1)
list[j] = list[j - 1];
list[i - 1] = e;
length++;
return true;
}
}
在执行插入操作时,插入元素的位置 i 的合法范围应该是1≤i≤L.length+1。当 i=1 时,插入位置在第一个元素之前,对应 Java 语言数组中的第 0 个元素,需要移动所有元素;当 i=L.length+1 时,插入位置在最后一个元素之后,对应 Java 语言数组中的最后一个元素之后的位置。当插入位置是 i=L.length+1 时,不需要移动元素。插入元素之前不仅要判断插入位置是否合法,还要判断顺序表的存储空间是否已满,在插入元素之后要将表长增加 1。
5) 删除操作
删除操作就是将顺序表 L 中的第 i 个位置的元素删除,顺序表的长度也由 n 变成 n-1。为了删除顺序表中的第 i 个元素,需要将第 i+1 个位置之后的元素依次向前移动一个位置,即先将第 i+1 个元素移动到第 i 个位置,再将第 i+2 个元素移动到第 i+1 个位置,以此类推,直到将最后一个元素移动到倒数第二个位置。最后将顺序表的长度减 1。
例如,要删除顺序表 {3,15,49,20,22,23,44,18,36} 的第 4 个元素,需要将序号为 5、6、7、8、9 的元素依次向前移动一个位置,这样就删除了第 4 个元素,最后将表长减 1,如下图所示。

图 3 在顺序表中删除元素20的过程
public boolean DeleteList(int i)
{
if (ListEmpty()) {
System.out.println("顺序表为空,不能进行删除操作!");
return false;
} else if (i >= 1 && i < length) {
for (int j = i; j < length; j++)
list[j - 1] = list[j];
length -= 1;
return true;
} else
return false;
}
删除元素的位置 i 的合法范围应该是1≤i≤L.length。当 i=1 时,表示删除第一个元素(对应 Java 数组中下标为 0 的元素);当 i=L.length 时,表示删除最后一个元素。在删除元素时,首先要判断顺序表中是否有元素,其次要判断要删除的元素的序号是否合法。删除成功后,将顺序表的长度减 1。
6) 求顺序表的长度
public int ListLength()
{
return length;
}
7) 清空顺序表
public void ClearList()
{
length = 0;
}
基本操作性能分析
在以上顺序表的基本操作算法中,除了按内容查找、插入和删除外,算法的时间复杂度都为 O(1)。
在按内容查找的算法中,若要查找的元素在第一个位置,则需要比较一次;若要查找的元素在最后一个位置,则需要比较 n 次(n 为线性表的长度)。设 pi 为在第 i 个位置找到与 e 相等的元素的概率,假设在任何位置找到元素的概率相等,即 pi=1/n,则查找过程中需要比较的平均次数为:
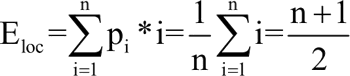
因此,按内容查找的平均时间复杂度为 O(n)。
在顺序表的插入算法中,时间的耗费主要集中在移动元素上。若要插入的元素在第一个位置,则需要移动元素的次数为 n;若要插入的元素在最后一个位置,则需要移动元素的次数为 1;若插入位置在最后一个元素之后,即第 n+1 个位置,则需要移动元素的次数为 0。设 pi 为在第 i 个位置插入元素的概率,假设在任何位置找到元素的概率相等,即 pi=1/(n+1),则顺序表的插入操作需要移动元素的平均次数为:
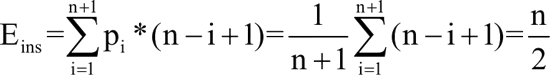
因此,插入操作的平均时间复杂度为 O(n)。
在顺序表的删除算法中,时间的耗费同样在移动元素上。若要删除的元素是第一个元素,则需要移动元素的次数为 n-1;若要删除的元素是最后一个元素,则需要移动元素的次数为 0。设 pi 表示删除第 i 个位置的元素的概率,假设在任何位置找到元素的概率相等,即 pi=1/n,则顺序表的删除操作需要移动元素的平均次数为:
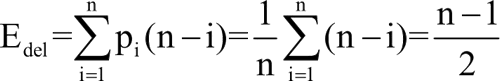
因此,删除操作的平均时间复杂度为 O(n)。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: