十进制转二进制(图文并茂,C语言实现)
在 C语言中,字节(byte)是计算机内存中的基本单位。一个字节通常由 8位(bit)组成,每个位可以表示 0 或 1。这种用 0 和 1 表示一个数字的方式,我们称之为二进制。
下图展示了这个过程:
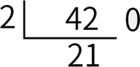
现在我们已经完成了一次短除运算,接下来将商作为新的被除数,重复上述步骤。下图显示了完整的短除法计算结果。
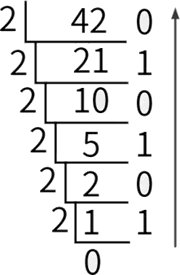
最后,我们从下往上逆序读右侧的余数 101010。这就是十进制数 42 对应的二进制数。
现在,我们可以将这个二进制数转换回十进制数,验证它是否等于 42。要将二进制数转换为十进制数,我们可以将二进制数的各位乘以其所在位的位权,然后将所有乘法结果累加起来,得到转换后的十进制结果。
例如,对于二进制数 101010,高位在左,低位在右,如下图所示:

最低位的位权为 2 的 0 次方,此后的位权依次加 1 次方。高位具有更大的位权,低位具有较小的位权。从最高位开始:
将所有的乘法结果累加起来,得到其十进制表示:
编写一个名为 printBinary 的函数,该函数可以接收一个无符号字符类型的参数,并将其转换为二进制表示,然后进行输出。我们暂时将二进制位数限制为最多 8 位。代码如下:
接下来,我们尝试将十进制数 42 作为参数传递给函数 printBinary():
如果希望高位在前,低位在后,则需要逆序输出每一次计算的余数。
我们将参数 dec 的二进制表示存储在一个长度为 8 的字符数组 bits 中,每个数组元素分别保存每一位的二进制状态。在计算余数之后,我们不再直接进行输出,而是将余数存储在 bits 数组的 count 索引对应的元素中。随后,count 自增 1,以便将新的余数存储在下一个数组元素中。修改后的代码如下:
在这个改进的版本中,我们考虑了当参数 dec 为 0 时的情况。若 dec 为 0,原先的代码将无法进入 while(dec > 0)循环,因此没有输出。为了处理这种情况,我们可以直接在函数开头检查 dec 是否为 0,如果为 0,则直接输出 0 并返回。代码修改如下:
然后,我们考虑将 unsigned char 类型的变量 dec 的 8 个二进制位全部进行输出。在这个改进的版本中,我们将 bits 数组初始化为 0。在计算完余数后,从数组的最后一个元素开始逆序输出,直至数组的第一个元素。这样,我们不再需要对 dec 为 0 的情况进行特殊处理。当 dec 为 0 时,不会进入 while 循环,将直接输出 8 个 0。代码修改如下:
十进制和二进制之间的转换
为了将十进制数据转换为二进制数据,可以使用短除法。例如,将十进制数 42 转换为二进制数,可以按照以下步骤进行操作。- 在被除数 42 的左下角写上符号 |___,表示将对其进行短除运算;
- 在符号 |___ 的左边写上除数 2;
- 计算被除数除以除数的商和余数:42 / 2 = 21 ... 0;
- 将商 21 填入符号 |___ 下方,将余数 0 填入右侧。
下图展示了这个过程:
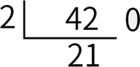
现在我们已经完成了一次短除运算,接下来将商作为新的被除数,重复上述步骤。下图显示了完整的短除法计算结果。

最后,我们从下往上逆序读右侧的余数 101010。这就是十进制数 42 对应的二进制数。
现在,我们可以将这个二进制数转换回十进制数,验证它是否等于 42。要将二进制数转换为十进制数,我们可以将二进制数的各位乘以其所在位的位权,然后将所有乘法结果累加起来,得到转换后的十进制结果。
例如,对于二进制数 101010,高位在左,低位在右,如下图所示:

最低位的位权为 2 的 0 次方,此后的位权依次加 1 次方。高位具有更大的位权,低位具有较小的位权。从最高位开始:
- 第 1 位的位权为 25,该位为 1,积为 25;
- 第 2 位的位权为 24,该位为 0,积为 0;
- 第 3 位的位权为 23,该位为 1,积为 23;
- 第 4 位的位权为 22,该位为 0,积为 0;
- 第 5 位的位权为 21,该位为 1,积为 21;
- 第 6 位的位权为 20,该位为 0,积为 0。
将所有的乘法结果累加起来,得到其十进制表示:
25 + 23 + 21 = 32 + 8 + 2 = 42
C语言实现十进制转二进制
接下来,我们将把十进制转二进制的过程编写成程序。编写一个名为 printBinary 的函数,该函数可以接收一个无符号字符类型的参数,并将其转换为二进制表示,然后进行输出。我们暂时将二进制位数限制为最多 8 位。代码如下:
void printBinary(unsigned char dec)
{
unsigned int quotient; // 商
unsigned int remainder; // 余数
while(dec > 0)
{
// 求除 2 的余数
remainder = dec % 2;
// 求除 2 的商
quotient = dec / 2;
// 输出商
printf("%d", remainder);
// 商作为新的被除数
dec = quotient;
}
putchar('\n');
}
在这个程序中,变量 dec 表示短除法运算中的被除数。变量 quotient 用于存储除以 2 的商,变量 remainder 用于存储除以 2 的余数。每次计算后,我们使用 printf() 输出余数,然后使用商作为新的被除数继续进行短除法运算,直至被除数为 0。接下来,我们尝试将十进制数 42 作为参数传递给函数 printBinary():
printBinary(42);运行程序后,输出结果为 010101,由于上述代码中是按照顺序输出余数的,所以输出结果是低位在前,高位在后。
如果希望高位在前,低位在后,则需要逆序输出每一次计算的余数。
我们将参数 dec 的二进制表示存储在一个长度为 8 的字符数组 bits 中,每个数组元素分别保存每一位的二进制状态。在计算余数之后,我们不再直接进行输出,而是将余数存储在 bits 数组的 count 索引对应的元素中。随后,count 自增 1,以便将新的余数存储在下一个数组元素中。修改后的代码如下:
void printBinary(unsigned char dec)
{
// 存储 dec 的每一位二进制状态
char bits[8];
int count = 0;
int quotient; // 商
int remainder; // 余数
while(dec > 0)
{
// 求除以 2 的余数
remainder = dec % 2;
// 求除以 2 的商
quotient = dec / 2;
// 商作为新的被除数
dec = quotient;
// 将余数保存到 bits
bits[count] = remainder;
count++;
}
// 逆序输出有数据的二进制位
for (int i = count - 1; i >= 0; i--)
printf("%d", bits[i]);
}
在循环结束后,共有 count 个二进制位被存储在 bits 数组中。从数组的 count - 1 索引开始,逆序输出这些二进制位,直至索引 0,即可得到从高位到低位的转换结果。运行结果输出 101010。在这个改进的版本中,我们考虑了当参数 dec 为 0 时的情况。若 dec 为 0,原先的代码将无法进入 while(dec > 0)循环,因此没有输出。为了处理这种情况,我们可以直接在函数开头检查 dec 是否为 0,如果为 0,则直接输出 0 并返回。代码修改如下:
void printBinary(unsigned char dec)
{
// 若 dec 为 0,输出 0 并返回
if (dec == 0)
{
printf("0\n");
return;
}
// 若 dec 非 0,短除计算余数,逆序输出
char bits[8];
int count = 0;
int quotient;
int remainder;
while(dec > 0)
{
remainder = dec % 2;
quotient = dec / 2;
dec = quotient;
bits[count] = remainder;
count++;
}
for (int i = count - 1; i >= 0; i--)
printf("%d", bits[i]);
putchar('\n');
}
然后,我们考虑将 unsigned char 类型的变量 dec 的 8 个二进制位全部进行输出。在这个改进的版本中,我们将 bits 数组初始化为 0。在计算完余数后,从数组的最后一个元素开始逆序输出,直至数组的第一个元素。这样,我们不再需要对 dec 为 0 的情况进行特殊处理。当 dec 为 0 时,不会进入 while 循环,将直接输出 8 个 0。代码修改如下:
void printBinary(unsigned char dec)
{
// 数组初始化为 0
char bits[8] = {0};
int count = 0;
int quotient;
int remainder;
while(dec > 0)
{
remainder = dec % 2;
quotient = dec / 2;
dec = quotient;
bits[count] = remainder;
count++;
}
// 逆序输出所有二进制位
for (int i = 8 - 1; i >= 0; i--)
printf("%d", bits[i]);
putchar('\n');
}
运行结果为 00101010,数据二进制最高位前的两个 0 也被输出了。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: