中序遍历二叉树详解(图文并茂,C语言实现)
中序遍历指首先中序遍历左子树,在左子树为空或已遍历时访问根,然后中序遍历右子树,即 LDR。若二叉树为空,则什么也不做。
1) 中序遍历 A 的左子树:
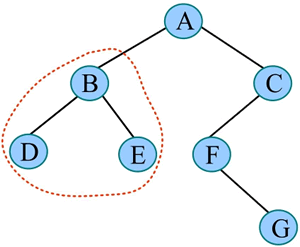
2) 中序遍历 B 的左子树:
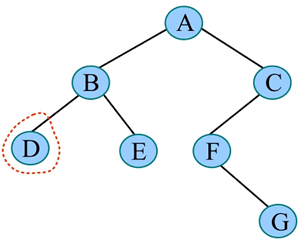
3) 中序遍历 D 的左子树,D 的左子树为空,访问 D,中序遍历 D 的右子树,D 的右子树也为空,返回 B:
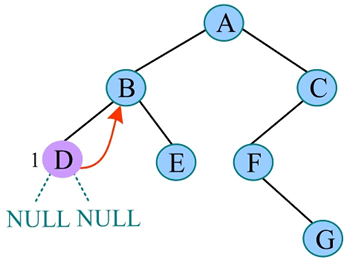
4) 访问 B,中序遍历 B 的右子树:
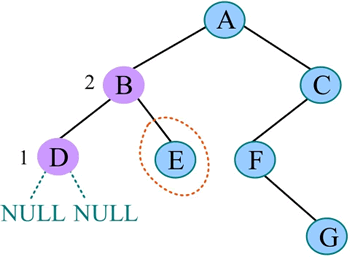
5) 中序遍历 E 的左子树,E 的左子树为空,访问 E,中序遍历 E 的右子树,E 的右子树也为空,返回 A:
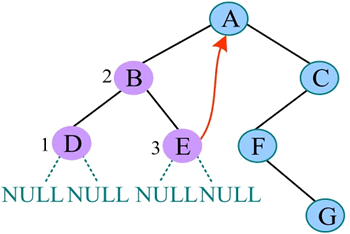
6) 访问 A,中序遍历 A 的右子树:
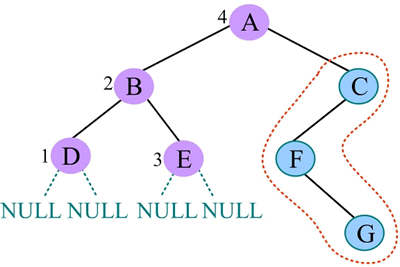
7) 中序遍历 C 的左子树:
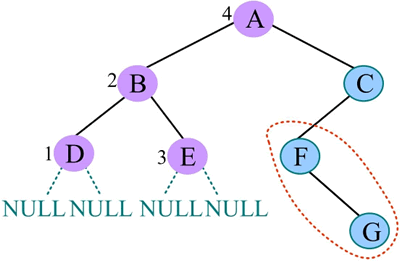
8) 中序遍历 F 的左子树,F 的左子树为空,访问 F,中序遍历 F 的右子树:
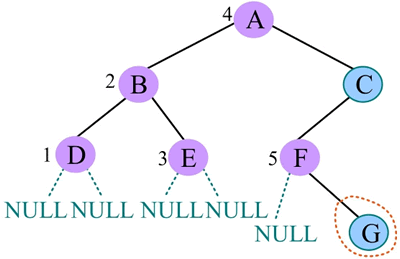
9) 中序遍历 G 的左子树,G 的左子树为空,访问 G,中序遍历 G 的右子树,G 的右子树也为空,返回 C:
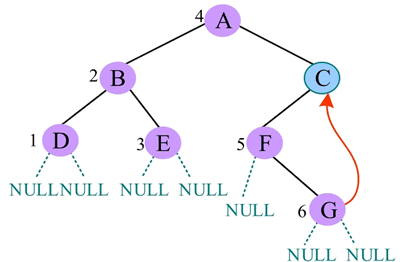
10) 访问 C,中序遍历 C 的右子树,G 的右子树为空,遍历结束:
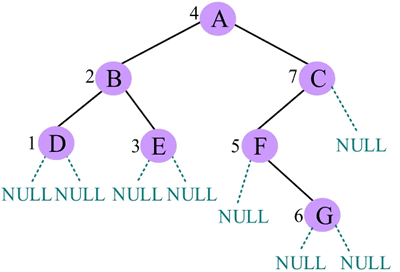 中序遍历序列为
中序遍历序列为
实现中序遍历二叉树的完整代码如下:
图解中序遍历二叉树的过程
一棵二叉树的中序遍历过程如下:1) 中序遍历 A 的左子树:

2) 中序遍历 B 的左子树:

3) 中序遍历 D 的左子树,D 的左子树为空,访问 D,中序遍历 D 的右子树,D 的右子树也为空,返回 B:

4) 访问 B,中序遍历 B 的右子树:

5) 中序遍历 E 的左子树,E 的左子树为空,访问 E,中序遍历 E 的右子树,E 的右子树也为空,返回 A:

6) 访问 A,中序遍历 A 的右子树:

7) 中序遍历 C 的左子树:

8) 中序遍历 F 的左子树,F 的左子树为空,访问 F,中序遍历 F 的右子树:

9) 中序遍历 G 的左子树,G 的左子树为空,访问 G,中序遍历 G 的右子树,G 的右子树也为空,返回 C:

10) 访问 C,中序遍历 C 的右子树,G 的右子树为空,遍历结束:

D B E A F G C。中序遍历的C语言实现
实现中序遍历二叉树的关键代码如下:
void inorder(Btree T) { //中序遍历
if(T) {
inorder(T->lchild);
cout << T->data << " ";
inorder(T->rchild);
}
}
实现中序遍历二叉树的完整代码如下:
#include <stdio.h>
#include <stdlib.h>
#define TElemType char
//构造结点的结构体
typedef struct BiTNode{
TElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
// 初始化树的函数
void CreateBiTree(BiTree *T) {
*T = (BiTNode *)malloc(sizeof(BiTNode)); // 创建根节点A
(*T)->data = 'A';
(*T)->lchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建左子节点B
(*T)->rchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建右子节点C
(*T)->lchild->data = 'B';
(*T)->lchild->lchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建B的左子节点D
(*T)->lchild->rchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建B的右子节点E
(*T)->rchild->data = 'C';
(*T)->rchild->lchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建C的左子节点F
(*T)->rchild->rchild = NULL; // C的右子节点为空
(*T)->lchild->lchild->data = 'D';
(*T)->lchild->lchild->lchild = NULL;
(*T)->lchild->lchild->rchild = NULL;
(*T)->lchild->rchild->data = 'E';
(*T)->lchild->rchild->lchild = NULL;
(*T)->lchild->rchild->rchild = NULL;
(*T)->rchild->lchild->data = 'F';
(*T)->rchild->lchild->lchild = NULL;
(*T)->rchild->lchild->rchild = (BiTNode *)malloc(sizeof(BiTNode));// 创建F的右子节点G
(*T)->rchild->lchild->rchild->data = 'G';
(*T)->rchild->lchild->rchild->lchild = NULL;
(*T)->rchild->lchild->rchild->rchild = NULL;
}
//模拟操作结点元素的函数,输出结点本身的数值
void displayElem(BiTNode* elem){
printf("%c ",elem->data);
}
//中序遍历
void INOrderTraverse(BiTree T){
if (T) {
INOrderTraverse(T->lchild);//遍历左孩子
displayElem(T);//调用操作结点数据的函数方法
INOrderTraverse(T->rchild);//遍历右孩子
}
//如果结点为空,返回上一层
return;
}
int main() {
BiTree Tree;
CreateBiTree(&Tree);
printf("中序遍历算法: \n");
INOrderTraverse(Tree);
}
运行结果为:
中序遍历算法: D B E A F G C
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: