随机森林算法详解(附带Python实例)
随机森林(Random Forest)是一种有监督学习算法,是以决策树为基学习器的集成学习算法。
随机森林非常简单,易于实现,计算开销也很小,但是它在分类和回归上表现出非常惊人的性能,因此,随机森林被誉为“代表集成学习技术水平的方法”。
随机森林,顾名思义就是树林,它包含大量的决策树并以此来辅助做出决定。随机森林中的每棵树的制作策略与单一决策相同。在做出决定时,所有小的决策树进行投票,并以多数票决定类别。
例如,在二元分类问题中,使用不同的设置可以创建数百个决策树。进行预测时,如果有 80% 的树决策为 A 类(从根节点移动到叶子节点),20% 的树决策为 B 类,则最终决策为 A 类。
使用随机森林而不是决策树是有优点的。随机森林可以处理丢失的数据。它们可以用于监督学习任务,同时也可以处理数据中的高维度数据。同样,使用多棵树而不是单一树减少了过拟合的可能性。
但随机森林也有一些缺点,其对模型几乎没有控制权。由于模型是树的组合,因此与单个决策树相比,随机森林的模型非常复杂;同时由于它是由数百或数千棵树组成的,因此难以解释。
因此,随机森林算法的主要流程为:
随机森林也称为集成方法。这些方法分而治之,它使用少量弱学习者来产生强学习者。在随机森林中,弱学习者是小树,加上多数投票的力量,使其成为强学习者。
用随机森林进行特征重要性评估的思想就是看每个特征在随机森林中的每棵树上做了多大的贡献,然后取个平均值,最后比一比特征之间的贡献大小。
贡献大小通常使用基尼指数(Gini Index)或者袋外数据(Out of Band,OOB)错误率作为评估指标来衡量。下面来学习一下基尼指数来评价的方法。
将变量重要性评分(Variable Importance Measures)用 VIM 来表示,将 Gini 指数用 GI 来表示,假设 m 个特征 x1,x2,…,xm,现在要计算出每个特征 xj 的 Gini 指数评分 VIMj(Gini) ,亦即第 j 个特征在 RF 所有决策树中节点分裂不纯度的平均改变量。
Gini 指数的计算公式为:
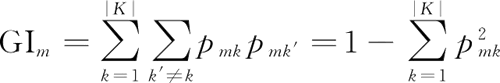
其中,K 表示有 K 个类别。pmk 表示节点 m 中类别 k 所占的比例。
直观地说,就是随机从节点 m 中抽取两个样本,其类别标记不一致的概率。
特征 xj 在节点 m 中的重要性,即节点 m 分支前后的 Gini 指数变化量为:
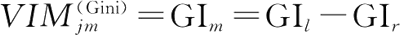
其中,GIl 和 GIr 分别表示分支后两个新节点的 Gini 指数。
如果特征 xj 在决策树 i 中出现的节点在集合 M 中,那么 xj 在第 i 棵树的重要性为:
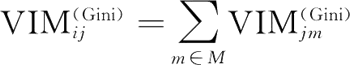
假设 RF 中共有 n 棵树,那么:
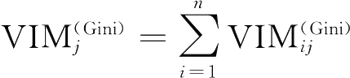
最后,把所有求得的重要性评分做归一化处理即可:
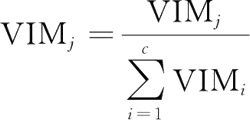
【实例 1】利用随机森林进行特征选择。
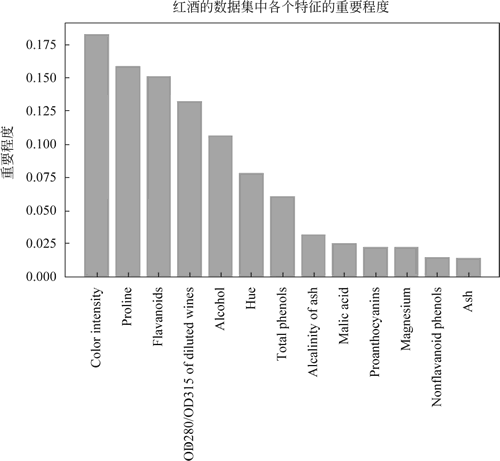
图 6 各特征效果图
【实例 2】利用SVR进行训练。
随机森林非常简单,易于实现,计算开销也很小,但是它在分类和回归上表现出非常惊人的性能,因此,随机森林被誉为“代表集成学习技术水平的方法”。
随机森林是什么
使用贪心算法在数据上创建一个单独的决策树,使用交叉验证技术来训练算法以避免过拟合。在决策树中,模型由一棵树的形式给出,通过从上到下遍历树来完成预测,并在叶子节点做出决策。随机森林,顾名思义就是树林,它包含大量的决策树并以此来辅助做出决定。随机森林中的每棵树的制作策略与单一决策相同。在做出决定时,所有小的决策树进行投票,并以多数票决定类别。
例如,在二元分类问题中,使用不同的设置可以创建数百个决策树。进行预测时,如果有 80% 的树决策为 A 类(从根节点移动到叶子节点),20% 的树决策为 B 类,则最终决策为 A 类。
使用随机森林而不是决策树是有优点的。随机森林可以处理丢失的数据。它们可以用于监督学习任务,同时也可以处理数据中的高维度数据。同样,使用多棵树而不是单一树减少了过拟合的可能性。
但随机森林也有一些缺点,其对模型几乎没有控制权。由于模型是树的组合,因此与单个决策树相比,随机森林的模型非常复杂;同时由于它是由数百或数千棵树组成的,因此难以解释。
因此,随机森林算法的主要流程为:
- 假设训练数据集中有 N 个记录。使用替换法从该数据集中选择 N 个记录创建样本。这意味着首先从 N 条记录中随机选择一条记录,然后再次从 N 条记录中选择一条记录。在这个策略中,记录可能会重复;
- 选择一个数字 m,该数字小于属性数量 K。它是在构建小型树时(m<K),从总属性中随机选择的属性数量;
- 使用不同样本,并且随机选择 m 个属性来建立 p 棵树;
- 在不剪枝的情况下,决策树增长直到所有属性完成或没有更多分割的可能性(只剩下一个类)为止;
- 通过对所有树进行多数表决来做出预测。
随机森林也称为集成方法。这些方法分而治之,它使用少量弱学习者来产生强学习者。在随机森林中,弱学习者是小树,加上多数投票的力量,使其成为强学习者。
特征重要评估
现实情况下,一个数据集中往往有成百上千个特征,如何在其中选择对结果影响最大的那几个特征,以此来缩减建立模型时的特征数是我们比较关心的问题。这样的方法其实很多,比如主成分分析,Lasso 等。不过这里我们学习的是用随机森林来进行特征筛选。用随机森林进行特征重要性评估的思想就是看每个特征在随机森林中的每棵树上做了多大的贡献,然后取个平均值,最后比一比特征之间的贡献大小。
贡献大小通常使用基尼指数(Gini Index)或者袋外数据(Out of Band,OOB)错误率作为评估指标来衡量。下面来学习一下基尼指数来评价的方法。
将变量重要性评分(Variable Importance Measures)用 VIM 来表示,将 Gini 指数用 GI 来表示,假设 m 个特征 x1,x2,…,xm,现在要计算出每个特征 xj 的 Gini 指数评分 VIMj(Gini) ,亦即第 j 个特征在 RF 所有决策树中节点分裂不纯度的平均改变量。
Gini 指数的计算公式为:
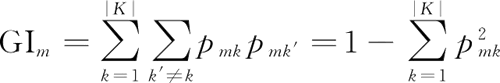
其中,K 表示有 K 个类别。pmk 表示节点 m 中类别 k 所占的比例。
直观地说,就是随机从节点 m 中抽取两个样本,其类别标记不一致的概率。
特征 xj 在节点 m 中的重要性,即节点 m 分支前后的 Gini 指数变化量为:
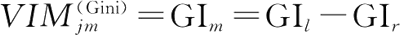
其中,GIl 和 GIr 分别表示分支后两个新节点的 Gini 指数。
如果特征 xj 在决策树 i 中出现的节点在集合 M 中,那么 xj 在第 i 棵树的重要性为:
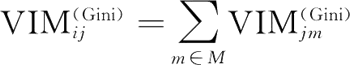
假设 RF 中共有 n 棵树,那么:
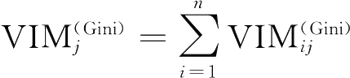
最后,把所有求得的重要性评分做归一化处理即可:
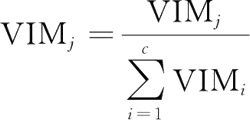
随机森林的实现
下面直接通过实例来演示随机森林的应用。【实例 1】利用随机森林进行特征选择。
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
# matplotlib inline
# url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data'
url = pd.read_csv('wine.data', header=None)
url.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
'Color intensity', 'Hue', 'OD280/OD315 of diluted wines', 'Proline']
#除去标签之外,共有13个特征,数据集的大小为178
#下面将数据集分为训练集和测试集
from sklearn.model_selection import train_test_split
print(type(url))
x, y = url.iloc[:, 1:].values, url.iloc[:, 0].values
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)
feat_labels = url.columns[1:]
# n_estimators:森林中树的数量
# n_jobs 为整数,可选 (默认=1),适合和预测并行运行的作业数,如果为-1,则将作业数设置为核心数
forest = RandomForestClassifier(n_estimators=10000, random_state=0, n_jobs=-1)
forest.fit(x_train, y_train)
#下面对训练好的随机森林,完成重要性评估
# feature_importances_ 可以调取关于特征重要程度
importances = forest.feature_importances_
print("重要性:", importances)
x_columns = url.columns[1:]
indices = np.argsort(importances)[::-1]
x_columns_indices = []
for f in range(x_train.shape[1]):
#对于最后需要逆序排序,做了类似决策树回溯的取值,从叶子收放
#到根,根据重要程度高于叶子
print("% 2d) %-*s %f" % (f + 1, 30, feat_labels[indices[f]], importances[indices[f]]))
x_columns_indices.append(feat_labels[indices[f]])
print(x_columns_indices)
print(x_columns.shape[0])
print(np.arange(x_columns.shape[0]))
#筛选变量(选择重要性比较高的变量)
threshold = 0.15
x_selected = x_train[:, importances > threshold]
#可视化
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.title("红酒的数据集中各个特征的重要程度", fontsize=18)
plt.ylabel("重要程度", fontsize=15, rotation=90)
plt.rcParams['font.sans-serif'] = ["SimHei"]
plt.rcParams['axes.unicode_minus'] = False
for i in range(x_columns.shape[0]):
plt.bar(i, importances[indices[i]], color='orange', align='center')
plt.xticks(np.arange(x_columns.shape[0]), x_columns_indices, rotation=90, fontsize=15)
plt.show()
运行程序,输出如下:
<class 'pandas.core.frame.DataFrame'>
重要性: [0.10658906 0.02539968 0.01391619 0.03203319 0.02207807 0.0607176
0.15094795 0.01464516 0.02235112 0.18248262 0.07824279 0.1319868
0.15860977]
1) Color intensity 0.182483
2) Proline 0.158610
3) Flavanoids 0.150948
4) OD280/OD315 of diluted wines 0.131987
5) Alcohol 0.106589
6) Hue 0.078243
7) Total phenols 0.060718
8) Alcalinity of ash 0.032033
9) Malic acid 0.025400
10) Proanthocyanins 0.022351
11) Magnesium 0.022078
12) Nonflavanoid phenols 0.014645
13) Ash 0.013916
['Color intensity', 'Proline', 'Flavanoids', 'OD280/OD315 of diluted wines',
'Alcohol', 'Hue', 'Total phenols', 'Alcalinity of ash', 'Malic acid',
'Proanthocyanins', 'Magnesium', 'Nonflavanoid phenols', 'Ash']
13
Index(['Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium',
'Total phenols', 'Flavanoids', 'Nonflavanoid phenols',
'Proanthocyanins', 'Color intensity', 'Hue',
'OD280/OD315 of diluted wines', 'Proline'],
dtype='object')
[ 0 1 2 3 4 5 6 7 8 9 10 11 12]
效果如下图所示:
图 6 各特征效果图
【实例 2】利用SVR进行训练。
from sklearn.svm import SVR # SVM中的回归算法
import pandas as pd
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
# 数据预处理,使得数据更加有效地被模型或者评估器识别
from sklearn import preprocessing
from sklearn.externals import joblib
# 获取数据
origin_data = pd.read_csv('wine.data', header=None)
X = origin_data.iloc[:, 1:].values
Y = origin_data.iloc[:, 0].values
print(type(Y))
# print(type(Y.values))
# 总特征。按照特征的重要性排序的所有特征
all_feature = [ 9, 12, 6, 11, 0, 10, 5, 3, 1, 8, 4, 7, 2]
# 此处选取前三个特征
topN_feature = all_feature[:3]
print(topN_feature)
# 获取重要特征的数据
data_X = X[:, topN_feature]
# 将每个特征值归一化到一个固定范围
# 原始数据标准化,为了加速收敛,最小最大规模化对原始数据进行线性变换,变换到[0,1]区间
data_X = preprocessing.MinMaxScaler().fit_transform(data_X)
# 利用 train_test_split 将训练集和测试集分开
X_train, X_test, y_train, y_test = train_test_split(data_X, Y, test_size=0.3)
# 通过多种模型预测
model_svrl = SVR(kernel='rbf', C=50, max_iter=10000)
# 训练
model_svrl.fit(X_train, y_train)
# 得分
score = model_svrl.score(X_test, y_test)
print(score)
运行程序,输出如下:
<class'numpy.ndarray'> [9,12,6] 0.9293427463178472
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: