随机森林算法(非常详细,附带实例)
随机森林就是通过集成学习的思想将多棵树集成的一种算法,它的基本单元是决策树,而它的本质属于机器学习的一大分支——集成学习(ensemble learning)方法。
把分别建立的多个决策树放到一起就是森林,这些决策树都是为了解决同一任务建立的,最终的目标也都是一致的,最后取其结果的平均即可,如下图所示。
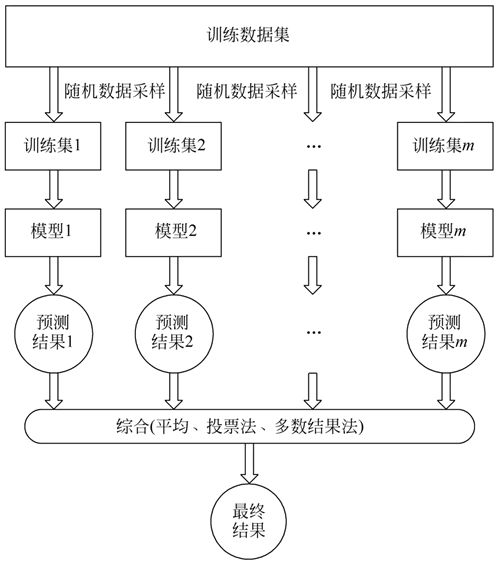
图 1 随机森林结构图
在随机森林中,数据是随机进行选取的,选取步骤如下:
如下图所示,假设随机森林中有 3 棵子决策树,2 棵子树的分类结果是 A 类,1 棵子树的分类结果是 B 类,那么随机森林的分类结果就是 A。

图 2 数据的随机选取
与数据集的随机选取类似,随机森林中的子树的每一个分裂过程并未用到所有的待选特征,而是从所有的待选特征中随机选取一定的特征,之后再在随机选取的特征中选取最优的特征。这样能使随机森林中的决策树都能彼此不同,提升系统的多样性,从而提升分类性能。
下图中,左边是一棵决策树的特征选取过程,通过在待选特征中选取最优的分裂特征,完成分裂。右边是一个随机森林中的子树的特征选取过程。

图 3 待选特征
随机森林算法的优点主要表现在以下几点:
随机森林算法的缺点主要表现在以下几点:
【实例】利用随机森林算法对 iris 数据集进行分类。

图 4 分类效果
把分别建立的多个决策树放到一起就是森林,这些决策树都是为了解决同一任务建立的,最终的目标也都是一致的,最后取其结果的平均即可,如下图所示。

图 1 随机森林结构图
随机森林的构建
随机森林算法实现步骤如下:- 一个样本容量为 N 的样本,有放回地抽取 N 次,每次抽取 1 个,最终形成了 N 个样本。选择好了的 N 个样本用来训练一个决策树,作为决策树根节点处的样本。
- 当每个样本有 M 个属性时,在决策树的每个节点需要分裂时,随机从这 M 个属性中选取出 m 个属性,满足条件 m≪M。然后从这 m 个属性中采用某种策略(如信息增益)来选择 1 个属性作为该节点的分裂属性。
- 决策树形成过程中每个节点都要按照步骤 2 来分裂(很容易理解,如果下一次该节点选出来的属性是刚刚其父节点分裂时用过的属性,则该节点已经达到了叶节点,无须继续分裂了),一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
- 按照步骤 1~3 建立大量的决策树,这样就构成了随机森林。
在随机森林中,数据是随机进行选取的,选取步骤如下:
- 从原始的数据集中采取有放回的抽样,构造子数据集,子数据集的数据量和原始数据集相同。不同子数据集的元素可以重复,同一个子数据集中的元素也可以重复。
- 利用子数据集构建子决策树,将这个数据放到每棵子决策树中,每棵子决策树输出一个结果。
- 如果有了新的数据,需要通过随机森林得到分类结果,通过对子决策树的判断结果的投票,得到随机森林的输出结果。
如下图所示,假设随机森林中有 3 棵子决策树,2 棵子树的分类结果是 A 类,1 棵子树的分类结果是 B 类,那么随机森林的分类结果就是 A。

图 2 数据的随机选取
与数据集的随机选取类似,随机森林中的子树的每一个分裂过程并未用到所有的待选特征,而是从所有的待选特征中随机选取一定的特征,之后再在随机选取的特征中选取最优的特征。这样能使随机森林中的决策树都能彼此不同,提升系统的多样性,从而提升分类性能。
下图中,左边是一棵决策树的特征选取过程,通过在待选特征中选取最优的分裂特征,完成分裂。右边是一个随机森林中的子树的特征选取过程。

图 3 待选特征
随机森林优缺点
跟其他算法相比,随机森林算法有其自身的优势与不足。随机森林算法的优点主要表现在以下几点:
- 它可以求出很高维度(特征很多)的数据,并且不用降维,无须做特征选择;
- 不容易过度拟合;
- 对于不平衡的数据集来说,它可以平衡误差;
- 如果有很大一部分的特征遗失,仍可以维持准确度。
随机森林算法的缺点主要表现在以下几点:
- 随机森林已经被证明在某些噪声较大的分类或回归问题上会过度拟合;
- 由于随机森林使用许多决策树,因此在较大的项目上可能需要大量内存,这使它比其他一些更有效的算法速度慢。
随机森林算法实战
前面已对随机森林算法的定义、构建、优缺点等进行了介绍,下面通过实战演示随机森林算法应用。【实例】利用随机森林算法对 iris 数据集进行分类。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
print('Class labels:', np.unique(y))
# 将数据分成 70 % 的训练数据和 30 % 的测试数据:
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.3, random_state = 1, stratify = y)
X_combined = np.vstack((X_train, X_test))
y_combined = np.hstack((y_train, y_test))
def plot_decision_regions(X, y, classifier, test_idx = None, resolution = 0.02):
# 设置标记生成器和颜色映射
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# 绘制决策面
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution) +
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha = 0.3, cmap = cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x = X[y == cl, 0],
y = X[y == cl, 1],
alpha = 0.8,
c = colors[idx],
marker = markers[idx],
label = cl,
edgecolor = 'black')
# 突出显示测试样本
if test_idx:
# 绘制所有样本
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0],
X_test[:, 1],
c = 'y',
edgecolor = 'black',
alpha = 1.0,
linewidth = 1,
marker = 'o',
s = 100,
label = 'test set')
forest = RandomForestClassifier(criterion = 'gini',
n_estimators = 25,
random_state = 1,
n_jobs = 2)
forest.fit(X_train, y_train)
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 中文
plot_decision_regions(X_combined, y_combined,
classifier = forest, test_idx = range(105, 150))
plt.xlabel('花瓣长度/cm')
plt.ylabel('花瓣宽度/cm')
plt.legend(loc = 'upper left')
plt.title('Random Forest')
plt.show()
运行程序,输出如下:
Class labels:[0 1 2]
效果如下图所示:
图 4 分类效果
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: