TensorBoard add_embedding()的用法(附带实例)
使用 add_embedding() 方法在二维或三维空间可视化 Embedding 向量,语法格式如下:
add_embedding() 是一个很实用的方法,不仅可以将高维特征使用 PCA、T-SNE 等方法降维至二维平面或三维空间显示,还可观察每一个数据点在降维前的特征空间的 K 近邻情况。下面取 MNIST 训练集中的 100 个数据,将图像展成一维向量直接作为 Embedding,使用 TensorBoardX 可视化出来。
示例代码如下:
这样,通过 SummaryWriter 可以将嵌入向量以及相关的信息记录下来,然后使用 TensorBoard 等工具进行可视化和分析。这种方式常用于可视化和监控模型学习到的特征表示。
可以发现,虽然还没有做任何特征提取的工作,但 MNIST 的数据已经呈现出聚类的效果,相同数字之间的距离更近一些(有没有想到 KNN 分类器)。我们还可以单击左下方的 T-SNE,用 T-SNE 的方法进行可视化。
使用 add_embedding 方法时需要注意以下几点:
采用 PCA 降维后,在三维空间的可视化结果如下图所示:
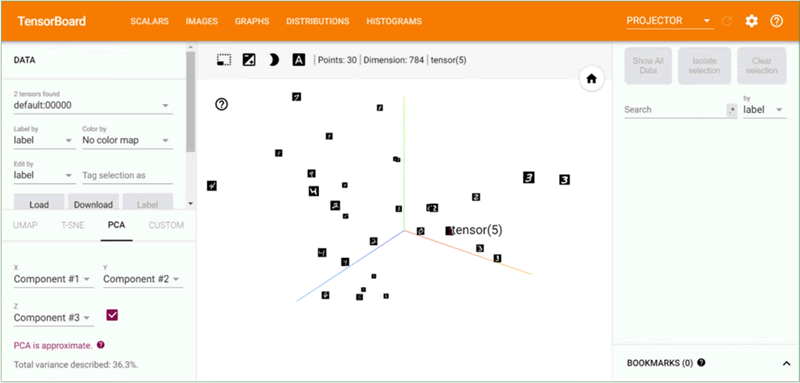
图 1 可视化向量
add_embedding(mat, metadata=None, label_img=None, global_step=None, tag='default', metadata_header=None)参数说明如下:
- mat (torch.Tensor or numpy.array):一个矩阵,每行代表特征空间的一个数据点;
- metadata (list or torch.Tensor or numpy.array, optional):一个一维列表,矩阵中每行数据的标签,大小应和矩阵行数相同;
- label_img (torch.Tensor, optional):一个形如 N×C×H×W 的张量,对应矩阵每一行数据显示出的图像,N 应和矩阵行数相同;
- global_step (int, optional):训练的步长;
- tag (string, optional):数据名称,不同名称的数据将分别展示。
add_embedding() 是一个很实用的方法,不仅可以将高维特征使用 PCA、T-SNE 等方法降维至二维平面或三维空间显示,还可观察每一个数据点在降维前的特征空间的 K 近邻情况。下面取 MNIST 训练集中的 100 个数据,将图像展成一维向量直接作为 Embedding,使用 TensorBoardX 可视化出来。
示例代码如下:
# 导入相关库
import torchvision
from tensorboardX import SummaryWriter
# 创建一个 SummaryWriter 对象,指定日志保存的路径为'runs/vector'
writer = SummaryWriter('runs/vector')
# 从 torchvision 中加载 MNIST 数据集,下载选项设置为 False
mnist = torchvision.datasets.MNIST('./', download=False)
# 添加嵌入向量
writer.add_embedding(
# 将 MNIST 数据集的图像数据转换为嵌入向量,并取前30个样本
mnist.data.reshape((-1, 28 * 28))[:30,:],
metadata=mnist.targets[:30], # 对应的标签
# 图像数据,用于显示每个嵌入向量对应的图像
label_img = mnist.data[:30,:,:].reshape((-1, 1, 28, 28)).float() / 255,
global_step=0 # 全局步骤
)
这段代码的主要目的是将 MNIST 数据集的一部分图像数据转换为嵌入向量,并将这些嵌入向量以及相关的元数据和图像添加到 SummaryWriter 中。这样,通过 SummaryWriter 可以将嵌入向量以及相关的信息记录下来,然后使用 TensorBoard 等工具进行可视化和分析。这种方式常用于可视化和监控模型学习到的特征表示。
可以发现,虽然还没有做任何特征提取的工作,但 MNIST 的数据已经呈现出聚类的效果,相同数字之间的距离更近一些(有没有想到 KNN 分类器)。我们还可以单击左下方的 T-SNE,用 T-SNE 的方法进行可视化。
使用 add_embedding 方法时需要注意以下几点:
- mat 是二维的(M×N),metadata 是一维的(N),label_img 是四维的(N×C×H×W);
- label_img 记得归一化为 0~1 的 float 值。
采用 PCA 降维后,在三维空间的可视化结果如下图所示:

图 1 可视化向量
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: