什么是优化器,PyTorch常见的优化器算法(非常详细)
优化器是深度学习中用于更新模型参数以最小化(或最大化)损失的算法。在深度学习和机器学习中,优化器的作用非常关键,它负责根据模型的性能指标(如损失函数)来调整模型的参数,以便找到最优的模型配置。
优化器的工作原理基于计算图上的梯度信息,通常遵循以下步骤:
常见的优化器有梯度下降(Gradient Descent)、随机梯度下降(Stochastic Gradient Descent,SGD)、标准动量优化算法(Momentum),以及一系列自适应学习率算法,如 AdaGrad、RMSprop 和 Adam 等。
例如,如果你需要从山上下来,如何选择下山的路径?这就需要根据周围的环境信息来选择。这个时候,可以利用梯度下降算法来帮助自己下山,以当前所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着下山的方向走,每走一段距离,反复采用同一个方法,如下图所示。

图 1 梯度下降
梯度下降的基本过程和下山的场景很类似。首先,我们有一个可微分的函数。这个函数就代表着一座山,我们的目标就是找到这个函数的最小值。对应到函数中,就是找到给定点的梯度,然后朝着梯度相反的方向,就能让函数值下降得最快。因为梯度的方向就是函数值变化最快的方向。所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。
梯度下降算法的公式如下:

α 在梯度下降算法中被称作学习率或步长,这意味着我们可以通过 α 来控制每一步走的距离,不能太大,也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点。
梯度前加一个负号,就意味着朝着梯度相反的方向前进。梯度的方向实际上就是函数在此点上升最快的方向,而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号。
常见的梯度下降算法有梯度下降(Full Gradient Descent)算法,随机梯度下降算法、随机平均梯度下降(Stochastic Average Gradient Descent)算法、小批量梯度下降(Mini-Batch Gradient Descent)算法。
1958 年,Rosenblatt 等研制出的感知机采用了随机梯度下降算法的思想,即每轮随机选取一个误分类样本,求其对应损失函数的梯度,再基于给定的步长更新参数。
1986年,Rumelhart 等分析了多层神经网络的误差反向传播算法,该算法每次按顺序或随机选取一个样本来更新参数,这实际上是小批量梯度下降法的一个特例。
批量梯度下降算法在梯度下降时,每次迭代都要计算整个训练数据上的梯度,当遇到大规模训练数据时,计算资源需求多,数据通常会非常冗余。随机梯度下降算法则把数据拆成几个小批次样本,每次只随机选择一个样本来更新神经网络参数。
实验表明,每次使用小批量样本,虽然不足以反映整体数据的情况,但却在很大程度上加速了神经网络的参数学习过程,并且不会丢失太多准确率。
对比批量梯度下降算法,假设从一批训练样本 n 中随机选取一个样本 is。模型参数为 W,代价函数为 J(W),梯度为 ΔJ(W),学习率为 ηt,则使用随机梯度下降算法更新参数表达式为:
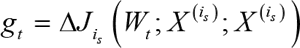
is ∈1,2,…,n 表示随机选择的一个梯度方向,Wt 表示 t 时刻的模型参数。E(gt )=ΔJ(Wt),这里虽然引入了随机性和噪声,但期望仍然等于正确的梯度下降。
该算法的优点是,虽然随机梯度下降算法需要走很多步的样子,但是对梯度的要求很低(计算梯度快)。而对于引入噪声,大量的理论和实践工作证明,只要噪声不是特别大,随机梯度下降算法都能很好地收敛。在应用大型数据集中,训练速度很快。比如每次从百万数据样本中取几百个数据点,计算一个随机梯度下降算法的梯度,更新一下模型参数。相比于标准梯度下降算法的遍历全部样本,每输入一个样本更新一次参数,要快得多。
该算法的缺点是,随机梯度下降算法在随机选择梯度的同时会引入噪声,使得权值更新的方向不一定正确。此外,随机梯度下降算法也没能单独克服局部最优解的问题。
这样,每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值,当某个参数在最近一段时间内的梯度方向不一致时,其真的参数更新幅度变小;相反,当在最近一段时间内的梯度方向都一致时,其真实的参数更新幅度变大,起到加速作用,相比随机梯度下降算法,能更快地达到最优。
动量主要解决随机梯度下降算法的两个问题:一是随机梯度的方法(引入的噪声);二是 Hessian 矩阵病态问题(可以理解为随机梯度下降算法在收敛过程中和正确梯度相比来回摆动比较大的问题)。
简单来说,由于当前权值的改变会受到上一次权值改变的影响,类似于小球向下滚动的时候带上了惯性。这样可以加快小球向下滚动的速度。
AdaGrad 算法借鉴正则化思想,每次迭代时自适应地调整每个参数的学习率,在进行第t次迭代时,先计算每个参数梯度平方的累计值,其表达式为:
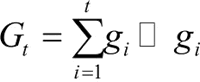
其中,⊙ 为按元素乘积,gt 是第 t 次迭代时的梯度。然后计算参数的更新差值,表达式为:
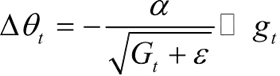
其中,α 是初始的学习率,ε 是为了保持数值稳定性而设置的非常小的常数。
在 AdaGrad 算法中,如果某个参数的偏导数累积比较大,其学习率相对较小;相反,如果其偏导数累积较小,其学习率相对较大。但整体随着迭代次数的增加,学习率逐渐缩小。
RMSProp 算法首先计算每次迭代梯度 gt 平方的指数衰减移动平均:
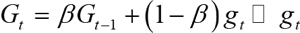
其中,β 为衰减率,然后用和 AdaGrad 算法同样的方法计算参数更新差值,从表达式中可以看出,RMSProp 算法的每个学习参数的衰减趋势既可以变小又可以变大。
RMSProp 算法在经验上已经被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习从业者经常采用的优化方法之一。
Adam 算法一方面计算梯度平方的指数加权平均(和 RMSprop 类似),另一方面计算梯度的指数加权平均(和 Momentum 法类似),其表达式为:
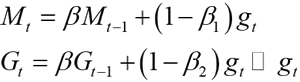
其中,β1 和 β2 分别为两个移动平均的衰减率,Adam 算法的参数更新差值为:
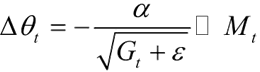
Adam 算法集合了 Momentum 算法和 RMSProp 算法的优点,因此相比之下,Adam 算法能更快、更好地找到最优值,迅速收敛。
以上我们介绍了几种常见的优化器算法,在实际应用中选择合适的优化器对于模型的训练至关重要,不同的优化器适用于不同的问题和场景。
在选择优化器时,需要考虑模型的复杂性、数据的特性以及训练的效率等因素。此外,还需要通过实验来调整优化器的学习率和其他超参数,以达到最佳的训练效果。
优化器的工作原理基于计算图上的梯度信息,通常遵循以下步骤:
- 计算损失:模型会对输入数据进行预测,并与真实值比较以计算出损失;
- 反向传播:使用链式法则(通过自动求导框架,如 PyTorch 的 .backward() 方法)计算损失相对于模型参数的梯度;
- 更新权重:优化器使用这些梯度来更新模型的权重。
常见的优化器有梯度下降(Gradient Descent)、随机梯度下降(Stochastic Gradient Descent,SGD)、标准动量优化算法(Momentum),以及一系列自适应学习率算法,如 AdaGrad、RMSprop 和 Adam 等。
梯度及梯度下降算法
梯度是微积分中一个很重要的概念,在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率,在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点上升最快的方向。例如,如果你需要从山上下来,如何选择下山的路径?这就需要根据周围的环境信息来选择。这个时候,可以利用梯度下降算法来帮助自己下山,以当前所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着下山的方向走,每走一段距离,反复采用同一个方法,如下图所示。

图 1 梯度下降
梯度下降的基本过程和下山的场景很类似。首先,我们有一个可微分的函数。这个函数就代表着一座山,我们的目标就是找到这个函数的最小值。对应到函数中,就是找到给定点的梯度,然后朝着梯度相反的方向,就能让函数值下降得最快。因为梯度的方向就是函数值变化最快的方向。所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。
梯度下降算法的公式如下:

α 在梯度下降算法中被称作学习率或步长,这意味着我们可以通过 α 来控制每一步走的距离,不能太大,也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点。
梯度前加一个负号,就意味着朝着梯度相反的方向前进。梯度的方向实际上就是函数在此点上升最快的方向,而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号。
常见的梯度下降算法有梯度下降(Full Gradient Descent)算法,随机梯度下降算法、随机平均梯度下降(Stochastic Average Gradient Descent)算法、小批量梯度下降(Mini-Batch Gradient Descent)算法。
随机梯度下降算法
随机梯度下降算法源于 1951 年 Robbins 和 Monro 提出的随机逼近,最初被应用于模式识别和神经网络。这种方法在迭代过程中随机选择一个或几个样本的梯度来替代总体梯度,从而大大降低了计算复杂度。1958 年,Rosenblatt 等研制出的感知机采用了随机梯度下降算法的思想,即每轮随机选取一个误分类样本,求其对应损失函数的梯度,再基于给定的步长更新参数。
1986年,Rumelhart 等分析了多层神经网络的误差反向传播算法,该算法每次按顺序或随机选取一个样本来更新参数,这实际上是小批量梯度下降法的一个特例。
批量梯度下降算法在梯度下降时,每次迭代都要计算整个训练数据上的梯度,当遇到大规模训练数据时,计算资源需求多,数据通常会非常冗余。随机梯度下降算法则把数据拆成几个小批次样本,每次只随机选择一个样本来更新神经网络参数。
实验表明,每次使用小批量样本,虽然不足以反映整体数据的情况,但却在很大程度上加速了神经网络的参数学习过程,并且不会丢失太多准确率。
对比批量梯度下降算法,假设从一批训练样本 n 中随机选取一个样本 is。模型参数为 W,代价函数为 J(W),梯度为 ΔJ(W),学习率为 ηt,则使用随机梯度下降算法更新参数表达式为:
Wt+1=Wt-ηtgt
其中: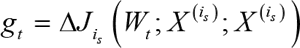
is ∈1,2,…,n 表示随机选择的一个梯度方向,Wt 表示 t 时刻的模型参数。E(gt )=ΔJ(Wt),这里虽然引入了随机性和噪声,但期望仍然等于正确的梯度下降。
该算法的优点是,虽然随机梯度下降算法需要走很多步的样子,但是对梯度的要求很低(计算梯度快)。而对于引入噪声,大量的理论和实践工作证明,只要噪声不是特别大,随机梯度下降算法都能很好地收敛。在应用大型数据集中,训练速度很快。比如每次从百万数据样本中取几百个数据点,计算一个随机梯度下降算法的梯度,更新一下模型参数。相比于标准梯度下降算法的遍历全部样本,每输入一个样本更新一次参数,要快得多。
该算法的缺点是,随机梯度下降算法在随机选择梯度的同时会引入噪声,使得权值更新的方向不一定正确。此外,随机梯度下降算法也没能单独克服局部最优解的问题。
标准动量优化算法
标准动量优化(Momentum)算法则将动量运用到神经网络的优化中,用累计的动量来替代真正的梯度,计算负梯度的“加权移动平均”来作为参数的更新方向,其参数更新表达式为:Δθt =ρΔθt-1-αgt
其中,ρ 为动量因子,通常设为 0.9,α 为学习率。这样,每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值,当某个参数在最近一段时间内的梯度方向不一致时,其真的参数更新幅度变小;相反,当在最近一段时间内的梯度方向都一致时,其真实的参数更新幅度变大,起到加速作用,相比随机梯度下降算法,能更快地达到最优。
动量主要解决随机梯度下降算法的两个问题:一是随机梯度的方法(引入的噪声);二是 Hessian 矩阵病态问题(可以理解为随机梯度下降算法在收敛过程中和正确梯度相比来回摆动比较大的问题)。
简单来说,由于当前权值的改变会受到上一次权值改变的影响,类似于小球向下滚动的时候带上了惯性。这样可以加快小球向下滚动的速度。
AdaGrad算法
在标准的梯度下降算法中,每个参数在每次迭代时都使用相同的学习率,AdaGrad 算法则改变了这一传统思想,由于每个参数维度上的收敛速度都不相同,因此根据不同参数的收敛情况分别设置学习率。AdaGrad 算法借鉴正则化思想,每次迭代时自适应地调整每个参数的学习率,在进行第t次迭代时,先计算每个参数梯度平方的累计值,其表达式为:
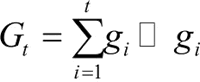
其中,⊙ 为按元素乘积,gt 是第 t 次迭代时的梯度。然后计算参数的更新差值,表达式为:
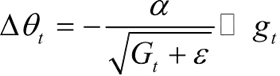
其中,α 是初始的学习率,ε 是为了保持数值稳定性而设置的非常小的常数。
在 AdaGrad 算法中,如果某个参数的偏导数累积比较大,其学习率相对较小;相反,如果其偏导数累积较小,其学习率相对较大。但整体随着迭代次数的增加,学习率逐渐缩小。
RMSProp算法
RMSProp 算法对 AdaGrad 算法进行了改进,在 AdaGrad 算法中由于学习率逐渐减小,在经过一定次数的迭代依然没有找到最优点时,便很难再继续找到最优点,RMSProp 算法则可在有些情况下避免这种问题。RMSProp 算法首先计算每次迭代梯度 gt 平方的指数衰减移动平均:
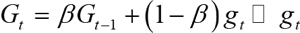
其中,β 为衰减率,然后用和 AdaGrad 算法同样的方法计算参数更新差值,从表达式中可以看出,RMSProp 算法的每个学习参数的衰减趋势既可以变小又可以变大。
RMSProp 算法在经验上已经被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习从业者经常采用的优化方法之一。
Adam算法
Adam 算法即自适应动量估计算法,是 Momentum 算法和 RMSProp 算法的结合,不但使用动量作为参数更新方向,而且可以自适应调整学习率。Adam 算法一方面计算梯度平方的指数加权平均(和 RMSprop 类似),另一方面计算梯度的指数加权平均(和 Momentum 法类似),其表达式为:
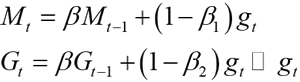
其中,β1 和 β2 分别为两个移动平均的衰减率,Adam 算法的参数更新差值为:
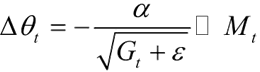
Adam 算法集合了 Momentum 算法和 RMSProp 算法的优点,因此相比之下,Adam 算法能更快、更好地找到最优值,迅速收敛。
以上我们介绍了几种常见的优化器算法,在实际应用中选择合适的优化器对于模型的训练至关重要,不同的优化器适用于不同的问题和场景。
在选择优化器时,需要考虑模型的复杂性、数据的特性以及训练的效率等因素。此外,还需要通过实验来调整优化器的学习率和其他超参数,以达到最佳的训练效果。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: