什么是激活函数,PyTorch常见的激活函数有哪些(非常详细)
在深度学习中,信号从一个神经元传入下一层神经元之前是通过线性叠加来计算的,而进入下一层神经元需要经过非线性的激活函数,继续往下传递,如此循环下去。由于这些非线性函数的反复叠加,才使得神经网络有足够的能力来抓取复杂的特征。
如果不使用非线性的激活函数,这种情况下每一层输出都是上一层输入的线性函数。无论神经网络有多少层,输出都是输入的线性函数,这样就和只有一个隐藏层的效果是一样的。这种情况相当于多层感知机(Multilayer Perceptron,MLP)。多层感知机是一种基础的前馈人工神经网络,用于解决分类和回归问题。
激活函数的发展经历了 Sigmoid->Tanh->ReLU->Leaky ReLU 等多种不同类型的及其改进结构,还有一个特殊的激活函数 Softmax,因为它只会被用在网络中的最后一层,所以主要用来进行最后的分类和归一化。
Sigmoid 函数常被用作神经网络的阈值函数,因为它在信息科学中具备单增、反函数单增等性质,所以它可以将变量映射到 0~1,其公式如下:
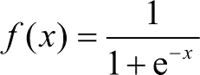
Sigmoid 是几十年来应用最多的激活函数之一,它的应用范围比较广泛,值域在 0 和 1 之间,因此可以将其输出作为预测二值型变量取值为 1 的概率,有很好的概率解释性。
Sigmoid 激活函数在其大部分定义域内都饱和,仅仅当输入接近 0 时才会对输入强烈敏感。它能够控制数值的幅度,并在深层网络中保持数据幅度不会出现大的变化。
绘制函数曲线的代码如下:
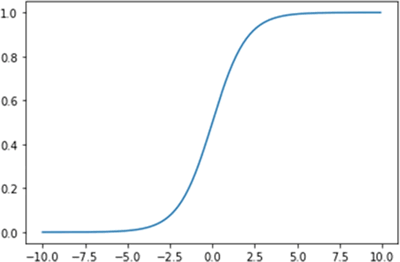
图 2 Sigmoid激活函数图形
Sigmoid 函数具有明显的优势,首先,Sigmoid 函数限定了神经元的输出范围为 0~1,在一些问题中,这种形式的输出可以被看作概率取值。其次,当神经网络的损失函数取交叉熵时,S 函数可用于输入数据的归一化操作,且交叉熵与 Sigmoid 函数的配合能够有效地改善算法迭代速度慢的问题。
在数学中,双曲正切是由基本双曲函数双曲正弦和双曲余弦推导而来的,其公式如下:
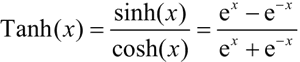
在分类任务中,Tanh 激活函数正逐渐取代 Sigmoid 激活函数成为神经网络的激活函数部分,根据图像可以看出,它关于原点对称,解决了 Sigmoid 函数中输出值都为正数的问题,而其他属性大多与 Sigmoid 函数相同,具有连续性和可微性。
绘制函数曲线的代码如下:
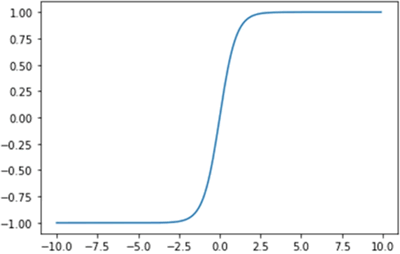
图 4 Tanh激活函数图形
Tanh 函数关于原点对称,是一个 0 均值的函数,这是它较之 Sigmoid 函数有所改进的地方。Sigmoid 函数的输出具有偏移现象,即输出均为大于 0 的实值。而 Tanh 的输出则均匀地分布在 y 轴两侧。生物神经元的激活具有稀疏性,而 Tanh 函数的输出结果更趋于 0,从而使人工神经网络更接近生物自然状态。
另外,ReLU 也是非 0 均值的激活函数,但是其本身具有的稀疏激活性在一定程度上可以抵消非 0 均值输出带来的影响。
绘制函数曲线的代码如下:
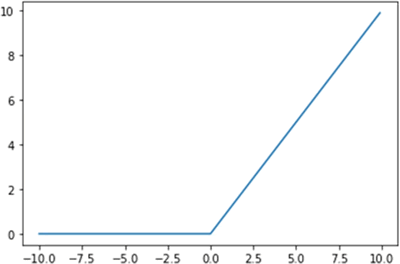
图 5 ReLU激活函数图形
ReLU 函数近年来应用较为广泛,相对于 Sigmoid 和 Tanh 函数,它解决了这两个函数存在的致命缺陷——梯度弥散问题。根据图像不难看出,函数在正无穷处的梯度是一个常量,而不是像前两个函数一样为 0,并且由于函数组成简单,因此运算速度比包含指数函数的 Sigmoid 和 Tanh 要快很多。
为了解决 ReLU 函数的这个缺点,在ReLU函数的负半区间引入了一个泄露(Leaky)值,所以称为 Leaky ReLU 函数,其公式如下:
绘制激活函数曲线的代码如下:
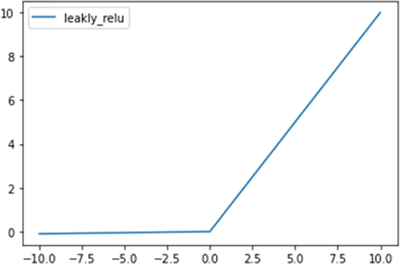
图 6 Leaky ReLU激活函数图形
如果不使用非线性的激活函数,这种情况下每一层输出都是上一层输入的线性函数。无论神经网络有多少层,输出都是输入的线性函数,这样就和只有一个隐藏层的效果是一样的。这种情况相当于多层感知机(Multilayer Perceptron,MLP)。多层感知机是一种基础的前馈人工神经网络,用于解决分类和回归问题。
激活函数的发展经历了 Sigmoid->Tanh->ReLU->Leaky ReLU 等多种不同类型的及其改进结构,还有一个特殊的激活函数 Softmax,因为它只会被用在网络中的最后一层,所以主要用来进行最后的分类和归一化。
Sigmoid激活函数
在生物学中,有一个常见的 S 型生长曲线,这就是 Sigmoid 函数。Sigmoid 函数常被用作神经网络的阈值函数,因为它在信息科学中具备单增、反函数单增等性质,所以它可以将变量映射到 0~1,其公式如下:
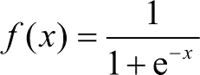
Sigmoid 是几十年来应用最多的激活函数之一,它的应用范围比较广泛,值域在 0 和 1 之间,因此可以将其输出作为预测二值型变量取值为 1 的概率,有很好的概率解释性。
Sigmoid 激活函数在其大部分定义域内都饱和,仅仅当输入接近 0 时才会对输入强烈敏感。它能够控制数值的幅度,并在深层网络中保持数据幅度不会出现大的变化。
绘制函数曲线的代码如下:
import numpy as np import matplotlib.pyplot as plt # 定义sigmoid函数,用于计算输入x的sigmoid值 def sigmoid(x): return 1. / (1. + np.exp(-x)) # 定义plot_sigmoid函数,用于绘制sigmoid函数图像 def plot_sigmoid(): # 生成x轴数据,范围为-10~10,步长为0.1 x = np.arange(-10, 10, 0.1) # 计算对应的y轴数据,即sigmoid值 y = sigmoid(x) # 绘制图像 plt.plot(x, y) # 显示图像 plt.show() # 程序入口 if __name__ == '__main__': plot_sigmoid()绘制的 Sigmoid 激活函数图形如下图所示:

图 2 Sigmoid激活函数图形
Sigmoid 函数具有明显的优势,首先,Sigmoid 函数限定了神经元的输出范围为 0~1,在一些问题中,这种形式的输出可以被看作概率取值。其次,当神经网络的损失函数取交叉熵时,S 函数可用于输入数据的归一化操作,且交叉熵与 Sigmoid 函数的配合能够有效地改善算法迭代速度慢的问题。
Tanh激活函数
Tanh 是双曲函数中的一个成员,它表示的是双曲正切函数。在数学中,双曲正切是由基本双曲函数双曲正弦和双曲余弦推导而来的,其公式如下:
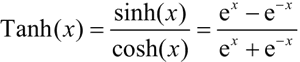
在分类任务中,Tanh 激活函数正逐渐取代 Sigmoid 激活函数成为神经网络的激活函数部分,根据图像可以看出,它关于原点对称,解决了 Sigmoid 函数中输出值都为正数的问题,而其他属性大多与 Sigmoid 函数相同,具有连续性和可微性。
绘制函数曲线的代码如下:
import numpy as np import matplotlib.pyplot as plt # 定义tanh函数,用于计算输入x的双曲正切值 def tanh(x): return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x)) # 定义plot_tanh函数,用于绘制tanh函数图像 def plot_tanh(): # 生成x轴数据,范围为-10~10,步长为0.1 x = np.arange(-10, 10, 0.1) # 计算对应的y轴数据,即tanh值 y = tanh(x) # 绘制图像 plt.plot(x, y) # 显示图像 plt.show() # 程序入口 if __name__ == '__main__': plot_tanh()绘制的 Tanh 激活函数图形如下图所示:

图 4 Tanh激活函数图形
Tanh 函数关于原点对称,是一个 0 均值的函数,这是它较之 Sigmoid 函数有所改进的地方。Sigmoid 函数的输出具有偏移现象,即输出均为大于 0 的实值。而 Tanh 的输出则均匀地分布在 y 轴两侧。生物神经元的激活具有稀疏性,而 Tanh 函数的输出结果更趋于 0,从而使人工神经网络更接近生物自然状态。
ReLU激活函数
2001 年,线性分段激活函数 ReLU(Rectified Linear Unit)首次被提出,伴随深度神经网络的产生而兴起,其公式如下:f(x)=max(0,x)ReLU 函数的一个直观特点就是形式简单,抑制所有小于 0 的输入,仅保留净激活大于 0 的部分。因此,当 x<0 时,函数的导数为 0,即 ReLU 在 x 轴右侧饱和。但与 Sigmoid 函数和 Tanh 函数同时存在左右两个饱和区的情况相比,ReLU 陷入单侧饱和的概率已经大大降低。
另外,ReLU 也是非 0 均值的激活函数,但是其本身具有的稀疏激活性在一定程度上可以抵消非 0 均值输出带来的影响。
绘制函数曲线的代码如下:
import numpy as np import matplotlib.pyplot as plt def relu(x): return np.maximum(0,x) def plot_relu(): x=np.arange(-10,10,0.1) y=relu(x) plt.plot(x,y) plt.show() if __name__ == '__main__': plot_relu()绘制的 ReLU 激活函数图形如下图所示:

图 5 ReLU激活函数图形
ReLU 函数近年来应用较为广泛,相对于 Sigmoid 和 Tanh 函数,它解决了这两个函数存在的致命缺陷——梯度弥散问题。根据图像不难看出,函数在正无穷处的梯度是一个常量,而不是像前两个函数一样为 0,并且由于函数组成简单,因此运算速度比包含指数函数的 Sigmoid 和 Tanh 要快很多。
Leaky ReLU激活函数
当 ReLU 的输入值为负的时候,输出始终为 0,其一阶导数也始终为 0,这样会导致神经元不能更新参数,也就是神经元不学习了,这种现象叫作“神经元坏死”。为了解决 ReLU 函数的这个缺点,在ReLU函数的负半区间引入了一个泄露(Leaky)值,所以称为 Leaky ReLU 函数,其公式如下:
f(x)=max(0.01x,x)带泄露修正线性单元的 Leaky ReLU 函数是经典(以及广泛使用的)的 ReLU 激活函数的变体,该函数输出对负值输入有很小的坡度。由于导数总是不为零,因此能够减少静默神经元的出现,允许基于梯度的学习(虽然会很慢),解决了 ReLU 函数进入负区间后,导致神经元不学习的问题。
绘制激活函数曲线的代码如下:
import numpy as np import matplotlib.pyplot as plt # 定义leaky_relu函数,用于计算输入x的Leaky ReLU值 def leaky_relu(x): return np.array([i if i > 0 else 0.01*i for i in x ]) # 定义lea_relu_diff函数,用于计算输入x的Leaky ReLU导数值 def lea_relu_diff(x): return np.where(x > 0, 1, 0.01) # 生成x轴数据,范围为-10~10,步长为0.01 x = np.arange(-10, 10, step=0.01) # 计算对应的y轴数据,即Leaky ReLU值 y_sigma = leaky_relu(x) # 计算对应的y轴数据,即Leaky ReLU导数值 y_sigma_diff = lea_relu_diff(x) # 创建一个子图 axes = plt.subplot(111) # 绘制Leaky ReLU曲线 axes.plot(x, y_sigma, label='leakly_relu') # 添加图例 axes.legend() # 显示图像 plt.show()绘制的 Leaky ReLU 激活函数图形如下图所示:

图 6 Leaky ReLU激活函数图形
其他类型的激活函数
除了前面介绍的 4 类激活函数外,PyTorch 2.2 中还有 24 类激活函数,如下表所示,具体用法和参数含义可以参考 PyTorch 官方文档的介绍。| 编号 | 激活函数 | 调用方法 |
|---|---|---|
| 1 | nn.ELU | torch.nn.ELU(alpha=1.0, inplace=False) |
| 2 | nn.Hardshrink | torch.nn.Hardshrink(lambd=0.5) |
| 3 | nn.Hardsigmoid | torch.nn.Hardsigmoid(inplace=False) |
| 4 | nn.Hardtanh | torch.nn.Hardtanh(min_val=-1.0, max_val=1.0, ...) |
| 5 | nn.Hardswish | torch.nn.Hardswish(inplace=False) |
| 6 | nn.LogSigmoid | torch.nn.LogSigmoid() |
| 7 | nn.MultiheadAttention | torch.nn.MultiheadAttention(embed_dim, num_heads, ...) |
| 8 | nn.PReLU | torch.nn.PReLU(num_parameters=1, init=0.25) |
| 9 | nn.ReLU6 | torch.nn.ReLU6(inplace=False) |
| 10 | nn.RReLU | torch.nn.RReLU(lower=0.125, upper=0.33, inplace=False) |
| 11 | nn.SELU | torch.nn.SELU(inplace=False) |
| 12 | nn.CELU | torch.nn.CELU(alpha=1.0, inplace=False) |
| 13 | nn.GELU | torch.nn.GELU() |
| 14 | nn.SiLU | torch.nn.SiLU(inplace=False) |
| 15 | nn.Softplus | torch.nn.Softplus(beta=1, threshold=-20) |
| 16 | nn.Softshrink | torch.nn.Softshrink(lambd=0.5) |
| 17 | nn.Softsign | torch.nn.Softsign() |
| 18 | nn.Tanhshrink | torch.nn.Tanhshrink() |
| 19 | nn.Threshold | torch.nn.Threshold(threshold, value, inplace=False) |
| 20 | nn.Softmin | torch.nn.Softmin(dim=None) |
| 21 | nn.Softmax | torch.nn.Softmax(dim=None) |
| 22 | nn.Softmax2d | torch.nn.Softmax2d() |
| 23 | nn.LogSoftmax | torch.nn.LogSoftmax(dim=None) |
| 24 | nn.AdaptiveLogSoftmaxWithLoss | torch.nn.AdaptiveLogSoftmaxWithLoss(...) |
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: