Prim普里姆算法求最小生成树(Java实现)
最小生成树是指在一个连通网的所有生成树中,其中所有边的代价之和最小的那棵生成树。代价在网中通过权值来表示,一棵生成树的代价就是生成树各边的代价之和。
例如要在 n 个城市建立一个交通图,就是要在 n(n-1)/2 条线路中选择 n-1 条代价最小的线路,各个城市可以看成是图的顶点,城市的线路可以看作图的边。
最小生成树具有一个重要的性质,假设一个连通网 N=(V,E),V 是顶点的集合,E 是边的集合,V 有一个非空子集 U。如果 (u,v) 是一条具有最小权值的边,其中 u∈U、v∈V-U,那么一定存在一个最小生成树包含边 (u,v)。
下面用反证法证明以上性质。假设所有的最小生成树都不存在这样的一条边 (u,v)。设 T 是连通网 N 中的一棵最小生成树,如果将边 (u,v) 加入 T 中,那么根据生成树的定义,T 一定出现包含 (u,v) 的回路。另外,T 中一定存在一条边 (u',v') 的权值大于或等于 (u,v) 的权值,若删除边 (u',v'),则得到一棵代价小于或等于 T 的生成树 T'。T' 是包含边 (u,v) 的最小生成树,这与假设矛盾。由此,以上性质得证。
最小生成树的构造算法有两个,分别是 Prim(普里姆)算法和 Kruskal(克鲁斯卡尔)算法,本节重点讲解 prim 算法。
这时,边集合 TE 一定有 n-1 条边,T={V,TE} 就是连通网 N 的最小生成树。
例如,如下图所示就是利用 Prim 算法构造最小生成树的过程。
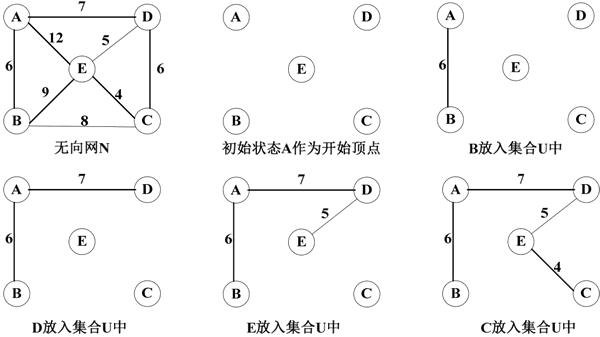
图 1 利用Prim算法构造最小生成树的过程
在实现算法时,需要设置一个数组 closeedge[MaxSize],用来保存 U 到 V-U 最小代价的边。对于每个顶点 v∈V-U,在数组中存在一个分量 closeedge[v],它包括两个域 adjvex 和 lowcost,其中,adjvex 域用来表示该边中属于 U 中的顶点,lowcost 域用来存储该边对应的权值。用公式描述如下:
根据 Prim 算法构造最小生成树,其对应过程中各个参数的变化情况如下表所示:
Prim 算法描述如下:
【实例】利用邻接矩阵创建一个如图 1 所示的无向网 N,然后利用 Prim 算法求该无向网的最小生成树。
分析如下:
主要考查 Prim 算法无向网的最小生成树算法。数组 closeedge 有两个域:adjvex 域和 lowcost 域:
因此,查找无向网 N 中的最小权值的边就是在数组 lowcost 中找到最小值,输出生成树的边后,要将新的顶点对应的数组值赋为 0,即将新顶点加入集合 U 中。以此类推,直到所有的顶点都加入集合 U 中。
数组 closeedge 中的 adjvex 域和 lowcost 域的变化情况如下图所示。
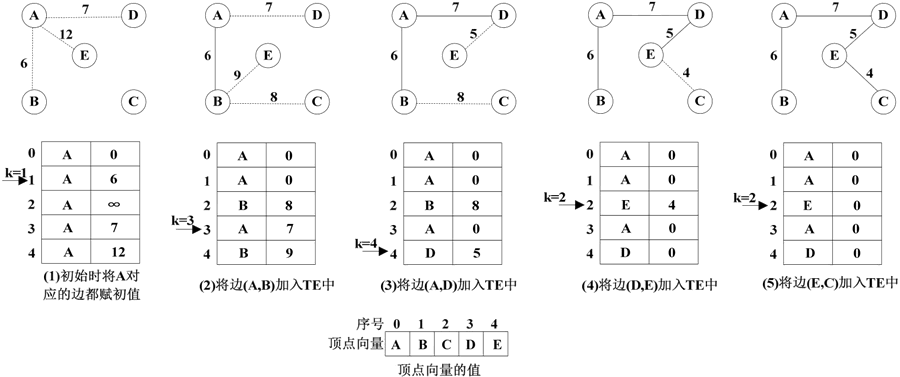
图 2 数组closeedge值的变化情况
根据 Prim 算法的思想,可根据给定的无向网构造最小生成树,其最小生成树算法实现如前面所述,求最小生成树的测试代码如下:
例如要在 n 个城市建立一个交通图,就是要在 n(n-1)/2 条线路中选择 n-1 条代价最小的线路,各个城市可以看成是图的顶点,城市的线路可以看作图的边。
最小生成树具有一个重要的性质,假设一个连通网 N=(V,E),V 是顶点的集合,E 是边的集合,V 有一个非空子集 U。如果 (u,v) 是一条具有最小权值的边,其中 u∈U、v∈V-U,那么一定存在一个最小生成树包含边 (u,v)。
下面用反证法证明以上性质。假设所有的最小生成树都不存在这样的一条边 (u,v)。设 T 是连通网 N 中的一棵最小生成树,如果将边 (u,v) 加入 T 中,那么根据生成树的定义,T 一定出现包含 (u,v) 的回路。另外,T 中一定存在一条边 (u',v') 的权值大于或等于 (u,v) 的权值,若删除边 (u',v'),则得到一棵代价小于或等于 T 的生成树 T'。T' 是包含边 (u,v) 的最小生成树,这与假设矛盾。由此,以上性质得证。
最小生成树的构造算法有两个,分别是 Prim(普里姆)算法和 Kruskal(克鲁斯卡尔)算法,本节重点讲解 prim 算法。
Prim算法
Prim 算法的具体描述是,假设 N={V,E} 是连通网,TE 是 N 的最小生成树的边的集合。执行以下操作:- 初始时,令 U={u0}(u0∈V)、TE=ϕ。
- 对于所有的边 u∈U,v∈V-U 的边 (u,v)∈E,将一条代价最小的边 (u0, v0) 放到集合 TE 中,同时将顶点 v0 放进集合 U 中。
- 重复执行第 2 个步骤,直到 U=V 为止。
这时,边集合 TE 一定有 n-1 条边,T={V,TE} 就是连通网 N 的最小生成树。
例如,如下图所示就是利用 Prim 算法构造最小生成树的过程。

图 1 利用Prim算法构造最小生成树的过程
- 初始时,集合 U={A},集合 V-U={B,C,D,E},边集合为 ϕ。
- A∈U 且 U 中只有一个元素,将 A 从 U 中取出,比较顶点 A 与集合 V-U 中顶点构成的代价最小边,在 (A,B)、(A,D)、(A,E) 中,最小的边是 (A,B)。将顶点 B 加入集合 U 中,边 (A,B) 加入 TE 中;
- U={A,B}、V-U={C,D,E}、TE=={(A,B)}。然后在集合 U 与集合 V-U 构成的所有边 (A,E)、(A,D)、(B,E)、(B,C) 中,其中最小边为 (A,D),故将顶点 D 加入集合 U 中,边 (A,D) 加入 TE 中,因此有 U={A,B,D}、V-U={C,E}、TE=={(A,B,D)};
- 以此类推,直到所有的顶点都加入 U 中。
在实现算法时,需要设置一个数组 closeedge[MaxSize],用来保存 U 到 V-U 最小代价的边。对于每个顶点 v∈V-U,在数组中存在一个分量 closeedge[v],它包括两个域 adjvex 和 lowcost,其中,adjvex 域用来表示该边中属于 U 中的顶点,lowcost 域用来存储该边对应的权值。用公式描述如下:
closeedge[v].lowcost=Min({cost(u,v)|u∈U})
根据 Prim 算法构造最小生成树,其对应过程中各个参数的变化情况如下表所示:
| i | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | U | V-U | k | (u0,v0) | ||
| closeedge[i] |
adjvex lowcost |
0 |
A 6 |
A ∞ |
A 7 |
A 12 |
{A} | {B,C,D,E} | 1 | (A,B) |
|
adjvex lowcost |
0 | 0 |
B 8 |
A 7 |
B 9 |
{A,B} | {C,D,E} | 3 | (A,D) | |
|
adjvex lowcost |
0 | 0 |
B 8 |
0 |
D 5 |
{A,B,D} | {C,E} | 4 | (D,E) | |
|
adjvex lowcost |
0 | 0 |
E 4 |
0 | 0 | {A,B,D,E} | {C} | 2 | (E,C) | |
|
adjvex lowcost |
0 | 0 | 0 | 0 | 0 | {A,B,D,E,C} | {} | |||
Prim 算法描述如下:
class CloseEdge
// 记录从顶点集合 U 到 v - U 的代价最小的边的定义
{
String adjvex;
double lowcost;
CloseEdge(String adjvex, double lowcost)
{
this.adjvex = adjvex;
this.lowcost = lowcost;
}
}
public class MinSpanningTree
{
public void Prim(MGraph M, String u, CloseEdge closedge[])
// 利用 Prim 算法求从第 u 个顶点出发构造网 G 的最小生成树
{
int k = M.LocateVertex(u); // k 为顶点 u 对应的序号
int m = 0;
for (int j = 0; j < M.vexnum; j++) // 数组初始化
{
CloseEdge close_edge = new CloseEdge(u, M.arc[k][j]);
closedge[m++] = close_edge;
}
closedge[k].lowcost = 0; // 初始时集合 U 只包括顶点 u
System.out.println("最小代价生成树的各条边为:");
for (int i = 1; i < M.vexnum; i++) // 选择剩下的 M.vexnum - 1 个顶点
{
k = MinNum(M, closedge); // k 为与 U 中顶点相邻接的下一个顶点的序号
System.print("(" + closedge[k].adjvex + "-" + M.vex[k] + ")");
// 输出生成树的边
closedge[k].lowcost = 0; // 第 k 个顶点并入 U 集
for (int j = 0; j < M.vexnum; j++) {
if (M.arc[k][j] < closedge[j].lowcost) // 新顶点加入 U 集后重新将最小边存入数组
{
closedge[j].adjvex = M.vex[k];
closedge[j].lowcost = M.arc[k][j];
}
}
}
}
}
Prim 算法中有两个嵌套的 for 循环,假设顶点的个数是 n,则第一层循环的频度为 n-1,第二层循环的频度为 n,因此该算法的时间复杂度为 O(n^2)。【实例】利用邻接矩阵创建一个如图 1 所示的无向网 N,然后利用 Prim 算法求该无向网的最小生成树。
分析如下:
主要考查 Prim 算法无向网的最小生成树算法。数组 closeedge 有两个域:adjvex 域和 lowcost 域:
- adjvex 域用来存放依附于集合 U 的顶点;
- lowcost 域用来存放数组下标对应的顶点到顶点(adjvex 中的值)的最小权值。
因此,查找无向网 N 中的最小权值的边就是在数组 lowcost 中找到最小值,输出生成树的边后,要将新的顶点对应的数组值赋为 0,即将新顶点加入集合 U 中。以此类推,直到所有的顶点都加入集合 U 中。
数组 closeedge 中的 adjvex 域和 lowcost 域的变化情况如下图所示。

图 2 数组closeedge值的变化情况
根据 Prim 算法的思想,可根据给定的无向网构造最小生成树,其最小生成树算法实现如前面所述,求最小生成树的测试代码如下:
public int MinNum(MGraph M, CloseEdge edge[])
// 将 lowcost 的最小值的序号返回
{
int i = 0;
while (edge[i].lowcost == 0) // 忽略数组中为 0 的值
i += 1;
double min = edge[i].lowcost; // min 为第一个不为 0 的值
int k = i;
for (int j = i + 1; j < M.vexnum; j++) {
if (edge[j].lowcost > 0 && edge[j].lowcost < min) // 将最小值对应的序号赋值给 k
{
min = edge[j].lowcost;
k = j;
}
}
return k;
}
public static void main(String args[]) {
System.out.println("创建一个无向网 N: ");
MGraph N = new MGraph();
N.CreateGraph2(Kind.UN);
System.out.println("输出网的顶点和弧: ");
N.DisplayGraph();
CloseEdge closedge[] = new CloseEdge[20];
MinSpanningTree MST = new MinSpanningTree();
MST.Prim(N, "A", closedge);
MST.Kruskal(N);
}
程序运行结果如下:
创建一个无向网 N:
请输入无向网 N 的顶点数, 弧数:
5 8
请输入 5 个顶点的值 (字符), 以空格分隔各个字符:
A B C D E
请输入 8 条弧的弧尾 弧头 权值 (以空格作为间隔):
A B 6
A D 7
A E 12
B C 8
B E 9
C D 6
C E 4
D E 5
输出网的顶点和弧:
有向网具有 5 个顶点 8 条弧,顶点依次是:A B C D E
有向网 N 的:
序号 i=
0 1 2 3 4
0 ∞ 6 ∞ 7 12
1 6 ∞ 8 ∞ 9
2 ∞ 8 ∞ 6 4
3 7 ∞ 6 ∞ 5
4 12 9 4 5 ∞
最小代价生成树的各条边为:
(A-B) (A-D) (D-E) (E-C)
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: