并查集详解(Java实现)
并查集(Disjoint Set Union)是一种主要用于处理互不相交的集合的合并和查询操作的树形结构。这种数据结构把一些元素按照一定的关系组合在一起。
关于并查集的运算,通常可采用树结构实现。其主要操作有并查集的初始化、查找 x 结点的根结点、合并 x 和 y。
并查集的基本运算如下表所示。
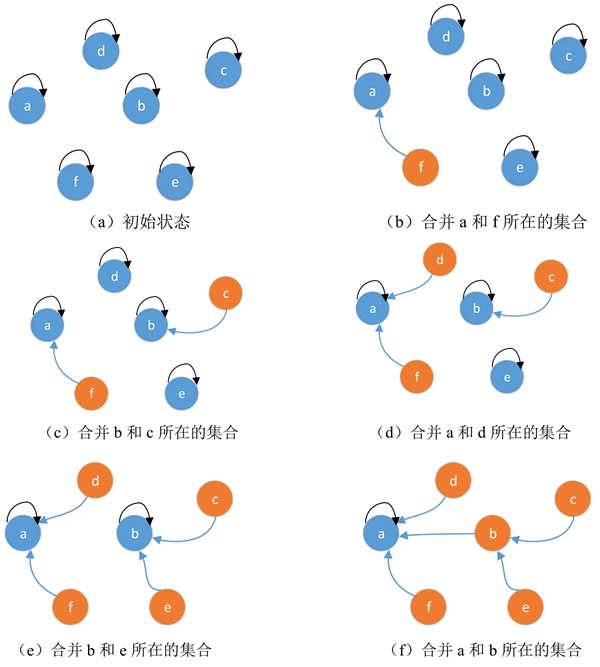
图 1 并查集的合并过程
将 b 和 c 所在的集合合并,使 b 成为父结点,如图 1(c)所示。继续将其他结点所在的集合合并,直到所有结点构成一棵树,如图 1(f)所示。
例如,查找结点 e 的根结点是沿着 e→b→a 路径找到根结点 a。
因此,可在查找的过程中使用路径压缩的方法,令查找路径上的结点逐个指向根结点,如下图所示。
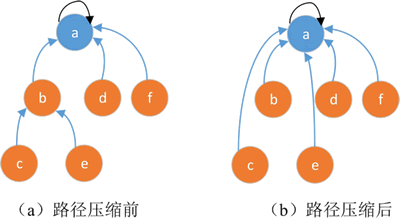
图 2 查找过程中的路径压缩
带路径压缩的查找算法实现如下:
为了方便理解,可将以上查找算法转换为以下非递归算法来实现:
两棵树合并后如下图所示:
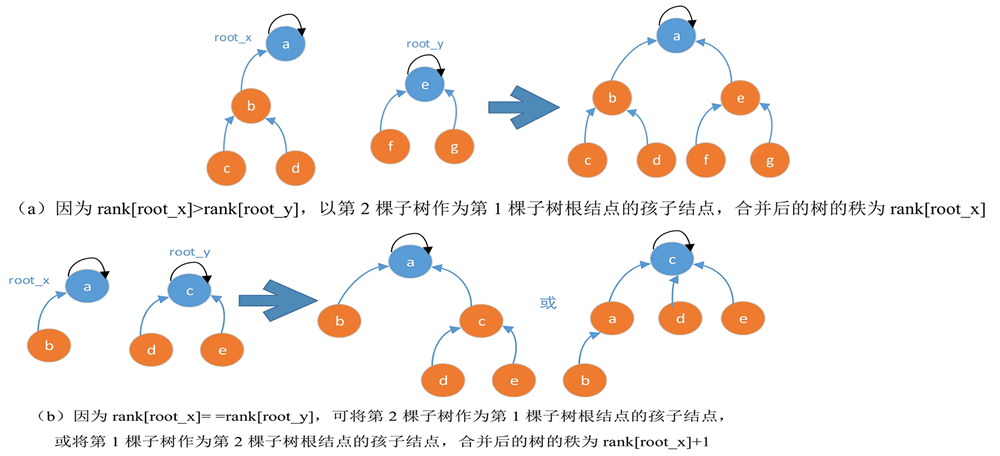
图 3 两棵子树的合并
合并算法实现如下:
判断包含 N 个顶点 M 条边的无向图是否为一棵树的充分必要条件是 N=M+1 且 N 个点连通。因此,关键在于判断这 N 个点是不是连通的。
判断连通性一般有两种方法:
算法实现如下:
并查集的定义
对于并查集,在一些有 N 个元素的集合应用问题中,初始时通常将每个元素看成是一个单元素的集合,然后按一定次序将属于同一组的元素所在的集合两两合并,其间要反复查找一个元素在哪个集合中。关于并查集的运算,通常可采用树结构实现。其主要操作有并查集的初始化、查找 x 结点的根结点、合并 x 和 y。
并查集的基本运算如下表所示。
| 基本操作 | 基本操作方法 |
|---|---|
| 初始化 | DisjointSet() |
| 查找 x 所属的集合(根结点) | Find(self,x) |
| 将 x 和 y 所属的两个集合(两棵树)合并 | Merge(self,x,y) |
并查集的实现
并查集的实现包括初始化、查找和合并操作。这些操作可以在一个类中实现。下面我们首先定义一个 DisjointSet 类。1) 初始化
初始化时,每个元素代表一棵树。假设有 n 个编号分别为 1,2,…,n 的元素,使用数组 parent 存储每个元素的父结点,初始化时,先将父结点设为自身。
public class DisjointSet {
final int MAXSIZE = 100;
int parent[];
int rank[];
DisjointSet(int n) {
parent = new int[n+1];
rank = new int[n+1];
for(int i = 0; i < n+1; i++)
parent[i] = i;
}
}
并查集的初始状态如图 1(a)所示。将 a 和 f 所在的集合(a 和 f 两棵树)合并后,使 a 成为两个结点构成的树的父结点,如图 1(b)所示。
图 1 并查集的合并过程
将 b 和 c 所在的集合合并,使 b 成为父结点,如图 1(c)所示。继续将其他结点所在的集合合并,直到所有结点构成一棵树,如图 1(f)所示。
2) 查找
查找操作是查找 x 结点所在子树的根结点。从图 1 可以看出,一棵子树的根结点满足条件:parent[y]=y。这可以通过不断顺着分支查找双亲结点找到,即 y=parent[y]。例如,查找结点 e 的根结点是沿着 e→b→a 路径找到根结点 a。
public int Find(int x) {
if (parent[x] == x)
return x;
else
return Find(parent[x]);
}
随着树的高度不断增加,想从终端结点找到根结点,其效率就会变得越来越低。有没有更好的办法呢?若每个结点都指向根结点,则查找效率会提高很多。因此,可在查找的过程中使用路径压缩的方法,令查找路径上的结点逐个指向根结点,如下图所示。

图 2 查找过程中的路径压缩
带路径压缩的查找算法实现如下:
public int Find2(int x) {
if (parent[x] == x)
return x;
parent[x] = Find2(x);
return parent[x];
}
为了方便理解,可将以上查找算法转换为以下非递归算法来实现:
public int Find_NonRec(int x) {
int root = x;
while (parent[root] != root) { // 查找根结点 root
root = parent[root];
}
int y = x;
while (y != root) { // 路径压缩
parent[y] = root;
y = parent[y];
}
return root;
}
经过以上路径压缩后,可以显著提高查找算法的效率。3) 合并
两棵树的合并操作就是将 x 和 y 所属的两棵子树合并为一棵子树。其合并算法的主要思想是,找到 x 和 y 所属子树的根结点 root_x 和 root_y,若 root_x==root_y,则表明它们属于同一棵子树,不需要合并;否则,需要比较两棵子树的高度,即秩,使合并后的子树的高度尽可能小:- 若 x 所在子树的秩 rank[root_x]<rank[root_y],则将秩较小的 root_x 作为 root_y 的孩子结点,此时 root_y 的秩不变。
- 若 x 所在子树的秩 rank[root_x]>rank[root_y],则将秩较小的 root_y 作为 root_x 的孩子结点,此时 root_x 的秩不变。
- 若 x 所在子树的秩 rank[root_x]==rank[root_y],则可将 root_x 作为 root_y 的孩子结点,也可将 root_y 作为 root_x 的孩子结点,合并后子树的秩加 1。
两棵树合并后如下图所示:

图 3 两棵子树的合并
合并算法实现如下:
public void Merge(int x, int y) {
int root_x = Find_NonRec(x);
int root_y = Find_NonRec(y); // 找到两个根结点
if (rank[root_x] <= rank[root_y]) // 若前者树的高度小于或等于后者
parent[root_x] = root_y;
else // 否则
parent[root_y] = root_x;
if (rank[root_x] == rank[root_y] && root_x != root_y) // 若高度相等且根结点不同,则新的根结点的高度 + 1
rank[root_y]++;
}
并查集的应用
给定一个包含 N 个顶点 M 条边的无向图 G,判断 G 是否为一棵树。判断包含 N 个顶点 M 条边的无向图是否为一棵树的充分必要条件是 N=M+1 且 N 个点连通。因此,关键在于判断这 N 个点是不是连通的。
判断连通性一般有两种方法:
- 利用图的连通性来判断。从一个顶点(比如 1 号顶点)开始进行深度或广度优先搜索遍历,搜索的过程中把遇到的顶点都进行标记,最后检查这 N 个顶点是否都被标记了。统计被标记顶点的数量是否等于 N,若为 N,则表明这是一棵树,否则不是一棵树。
- 用并查集的基本操作实现判断。依次搜索每条边,把每条边相关联的两个顶点都合并到一个集合中,最后检查是不是 N 个顶点都在同一个集合中。若 N 个顶点都在同一个集合中,则是一棵树,否则不是一棵树。
算法实现如下:
public int FindParent(int x, int parent[]) // 在并查集中查找 x 结点的根结点
{
if(x == parent[x])
return x;
parent[x] = FindParent(parent[x], parent);
return parent[x];
}
public static void main(String args[]) {
int SIZE = 100;
int parent[] = new int[SIZE];
System.out.println("请分别输入结点数和边数: ");
Scanner sc = new Scanner(System.in);
String str[] = sc.nextLine().split(" ");
int n = Integer.parseInt(str[0]);
int m = Integer.parseInt(str[1]);
boolean flag = false;
DisjointSet ds = new DisjointSet(n);
if (m != n - 1)
flag = true;
for(int i = 1; i < n + 1; i++)
parent[i] = i;
int iter = 1;
while (m != 0) {
System.out.print("请输入第" + iter + "条边对应的顶点:");
str = sc.nextLine().split(" ");
int x = Integer.parseInt(str[0]);
int y = Integer.parseInt(str[1]);
int fx = ds.FindParent(x, parent);
int fy = ds.FindParent(y, parent);
if (parent[fx] != parent[fy])
parent[fx] = parent[fy];
m--;
iter++;
}
int root = ds.FindParent(parent[1], parent);
for (int i = 2; i < n + 1; i++) {
if (ds.FindParent(parent[i], parent) != root) {
flag = true;
break;
}
}
if (flag)
System.out.println("这不是一棵树!");
else
System.out.println("这是一棵树!");
}
程序运行结果如下:
请分别输入结点数和边数:
5 4
请输入第 1 条边对应的顶点:1 2
请输入第 2 条边对应的顶点:1 3
请输入第 3 条边对应的顶点:2 4
请输入第 4 条边对应的顶点:2 5
这是一棵树!
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: