Python绘制矩阵散点图的多种方法（附带实例）

矩阵散点图（Matrix Scatter Plot）是一种用于可视化多个变量之间的关系的图表。它通过在一个矩阵中绘制多个散点图的组合来展示变量之间的相互作用和相关性。

矩阵散点图的优点是可以同时展示多个变量之间的关系，帮助我们观察和发现不同变量之间的模式、趋势和相关性。通过矩阵散点图，我们可以更全面地了解变量之间的相互作用，以发现潜在的关联和趋势。

然而，当变量数量较多时，矩阵散点图可能会变得复杂且难以解读。因此，在使用矩阵散点图时，应谨慎选择变量数量，并根据可视化目的选择合适的变量和展示方式，以确保图表的可读性和准确传达变量之间的关系。

在矩阵散点图中，每个变量都会沿着轴的方向占据一行或一列，图中的每个小格子代表一个变量对。对角线上的小格子通常展示的是该变量自身的分布情况，而其他位置的小格子则展示了两个变量之间的关系，即散点图。通过观察这些散点图，可以直观地了解各个变量之间的相关性、趋势以及异常值。

矩阵散点图对于探索性数据分析非常有用，因为它能够同时显示多个变量之间的关系，帮助研究人员发现变量之间的相互作用和规律。在数据集中存在多个变量时，使用矩阵散点图可以更全面地了解数据的特征，并为进一步的分析提供线索。

利用 Seaborn 库中的 pairplot() 函数可以绘制矩阵散点图。

【实例 1】绘制一个散点矩阵图，展示 iris 数据集中各个特征两两之间的关系，并根据花的种类进行着色区分。

# 导入 matplotlib.pyplot 模块
import matplotlib.pyplot as plt
# 导入 seaborn 模块
import seaborn as sns

df = sns.load_dataset('iris')          # 加载 iris 数据集
sns.pairplot(df, kind="reg")           # 绘制带回归线的矩阵散点图
plt.show()

sns.pairplot(df, kind="scatter")       # 绘制不带回归线的矩阵散点图
plt.show()

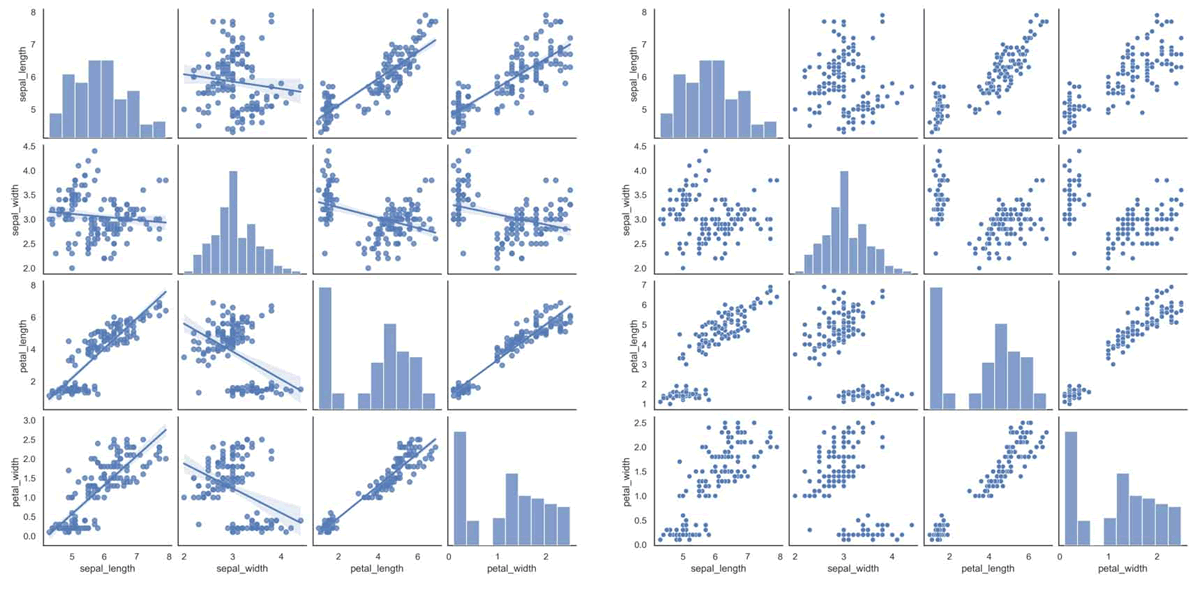
上述代码使用 Seaborn 库加载了 iris 数据集，并绘制了带有回归线和不带回归线的矩阵散点图。首先，通过 sns.load_dataset('iris') 加载了 iris 数据集。然后，分别使用 sns.pairplot(df,kind="reg") 和 sns.pairplot(df,kind="scatter") 绘制了带有回归线和不带回归线的矩阵散点图。

输出的结果如下图所示：

# 绘制左边图：矩阵散点图，并按照 'species' 列进行着色
sns.pairplot(df, kind="scatter", hue="species", # hue 定义数据子集的变量
             markers=["o", "s", "D"], # markers 标记形状列表
             palette="Set2") # palette 用于映射色调变量的颜色集
plt.show()

# 绘制右边图：矩阵散点图，并按照 'species' 列进行着色，同时设置绘图参数
sns.pairplot(df, kind="scatter", hue="species", plot_kws=dict(s=80, edgecolor="white", linewidth=2.5)) # plotkws 用于修改图形元素的关键字参数字典
plt.show()

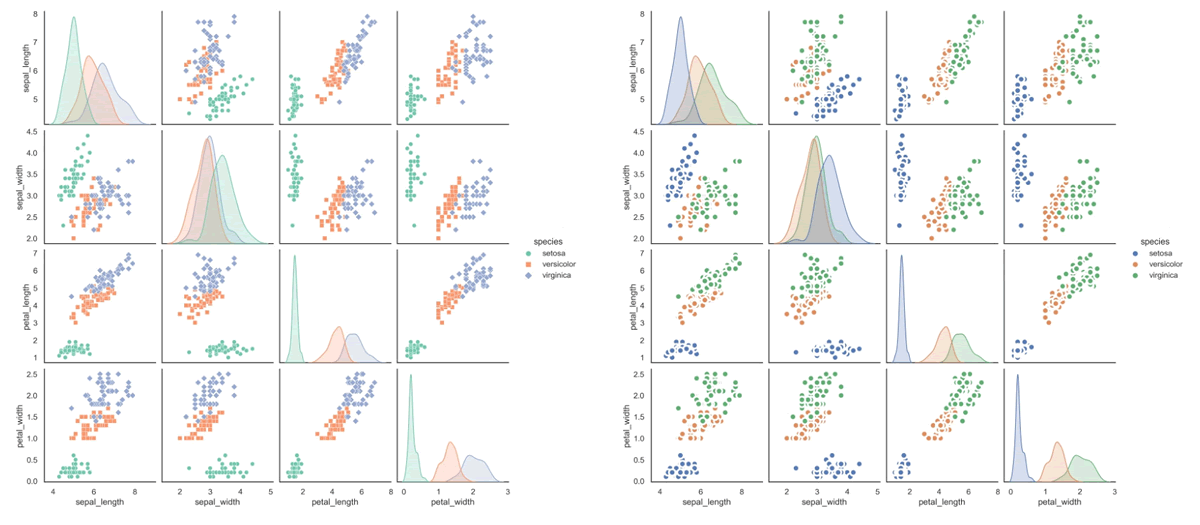
上述代码使用 Seaborn 库绘制了两个矩阵散点图：

左边的图根据 'species' 列进行着色，使用不同的标记形状和颜色集；
右边的图同样根据 'species' 列进行着色，并通过 plot_kws 参数自定义了标记的大小、边缘颜色和线宽。

输出的结果如下图所示：

# 绘制密度图矩阵
sns.pairplot(df, diag_kind="kde")
# 绘制直方图矩阵
sns.pairplot(df, diag_kind="hist")

# 将其自定义为密度图或直方图
sns.pairplot(df, diag_kind="kde",
             diag_kws=dict(shade=True, bw_adjust=.05, vertical=False))
# diag_kind 设置对角子图的类型（包括 'auto'、'hist'、'kde'、None）
plt.show()

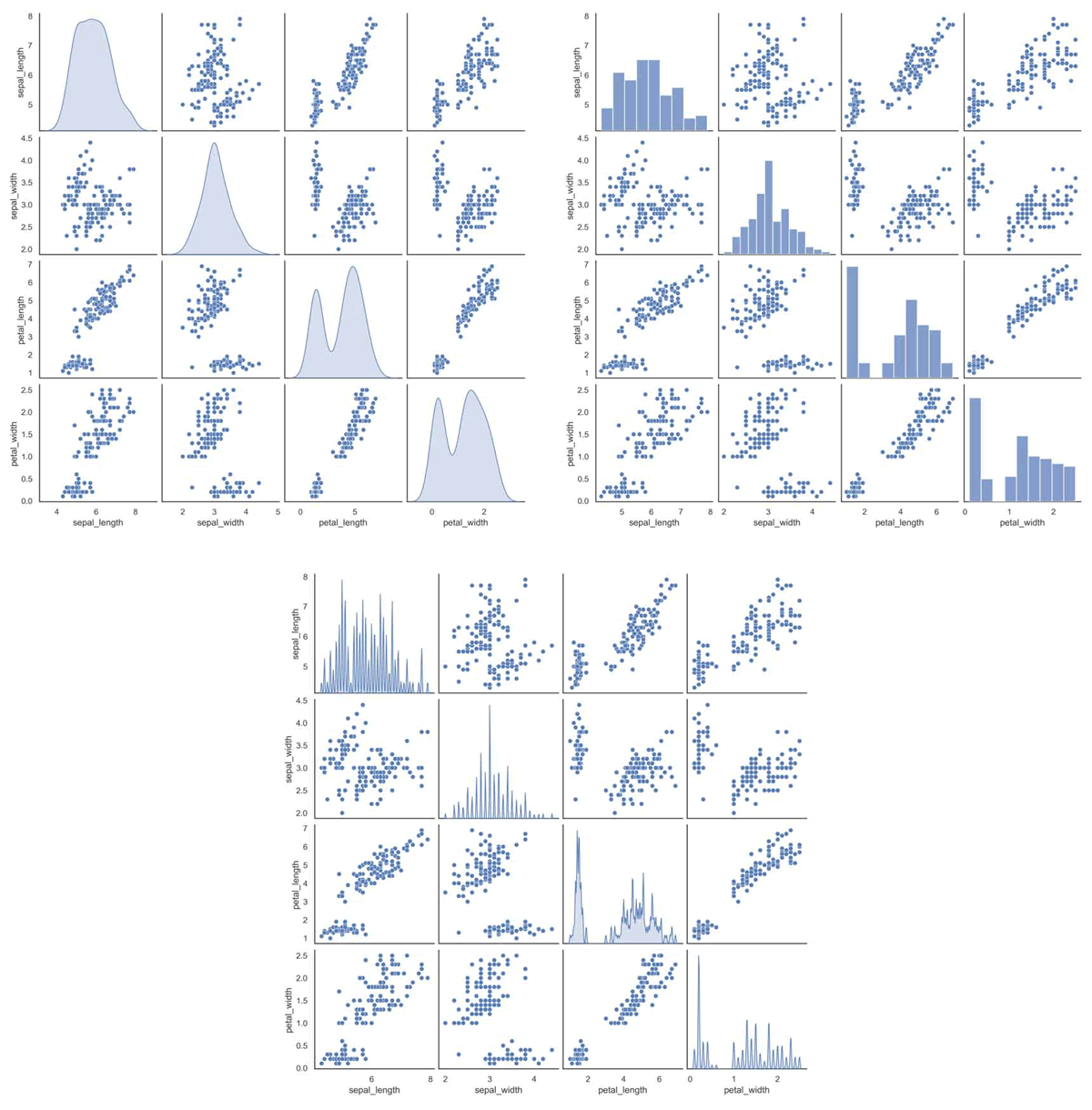
上述代码使用 Seaborn 库绘制了不同类型的对角子图矩阵，包括密度图矩阵、直方图矩阵以及自定义参数的密度图矩阵。输出的结果如下图所示：

【实例 2 】绘制一个散点矩阵图，展示 iris 数据集中各个特征两两之间的关系，并根据花的种类进行着色区分。

import matplotlib.pyplot as plt
from mlxtend.data import iris_data
from mlxtend.plotting import scatterplotmatrix

X, y = iris_data()
scatterplotmatrix(X, figsize=(10, 8))
plt.tight_layout()
plt.show()

names = ['sepal length [cm]', 'sepal width [cm]',
         'petal length [cm]', 'petal width [cm]']
fig, axes = scatterplotmatrix(X[y == 0], figsize=(10, 8), alpha=0.5)
fig, axes = scatterplotmatrix(X[y == 1], fig_axes=(fig, axes), alpha=0.5)
fig, axes = scatterplotmatrix(X[y == 2], fig_axes=(fig, axes), alpha=0.5, names=names)
plt.tight_layout()
plt.show()

上述代码使用 Mlxtend 库中的 scatterplotmatrix() 函数绘制了两个散点图矩阵。第一个散点图矩阵展示了 iris 数据集中所有特征的散点图关系。接着，根据类别标签绘制了三个子图矩阵，每个子图矩阵中展示了特定类别的样本点。

输出的结果如下图所示：

Python绘制矩阵散点图的多种方法（附带实例）

相关文章