堆排序(图文并茂,Java实现)
堆排序的算法思想主要是利用二叉树的性质进行排序。
堆排序是利用二叉树的树形结构,按照完全二叉树的编号次序,将元素序列的关键字依次存放在相应的结点。然后从叶子结点开始,从互为兄弟的两个结点中(没有兄弟结点的除外)选择一个较大(或较小)者与其双亲结点比较,若该结点大于(或小于)双亲结点,则将两者进行交换,使较大(或较小)者成为双亲结点。
对所有的结点都进行类似操作,直到根结点为止。此时,根结点的元素值的关键字最大(或最小)。这样就构成了堆,堆中的每一个结点都大于(或小于)其孩子结点。
堆的数学形式定义为:假设存在 n 个元素,其关键字序列为 (k1,k2,…,ki,…,kn),如果有:
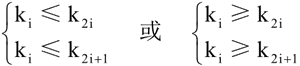
其中 i=1,2,...,⌊n/2⌋,称此元素序列构成了一个堆。
若将这些元素的关键字存放在数组中,将此数组中的元素与完全二叉树一一对应起来,则完全二叉树中的每个非叶子结点的值都不小于(或不大于)孩子结点的值。
在堆中,堆的根结点元素值一定是所有结点元素值的最大值或最小值。例如,序列 (87,64,53,51,23,21,48,32) 和 (12,35,27,46,41,39,48,55,89,76)都是堆,相应的完全二叉树表示如下图所示:
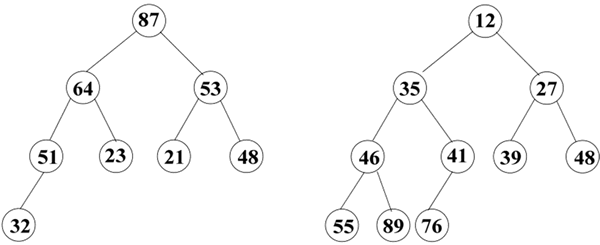
图 2 大顶堆和小顶堆
在图 2 中,一个是非叶子结点的元素值不小于其孩子结点的元素值,这样的堆称为大顶堆;另一个是非叶子结点的元素值不大于其孩子结点的元素值,这样的堆称为小顶堆。
若将堆中的根结点(堆顶)输出之后,将剩余的 n-1 个结点的元素值重新建立一个堆,则新堆的堆顶元素值是次大(或次小)值,将该堆顶元素输出。然后将剩余的 n-2 个结点的元素值重新建立一个堆,反复执行以上操作,直到堆中没有结点,就构成了一个有序序列,这样的重复建堆并输出堆顶元素的过程称为堆排序。
假设将待排序的元素的关键字存放在数组 a 中,第 1 个元素的关键字 a[1] 表示二叉树的根结点,剩下的元素的关键字 a[2…n] 分别与二叉树中的结点按照层次从左到右一一对应。
例如,根结点的左孩子结点存放在 a[2] 中,右孩子结点存放在 a[3] 中,a[i] 的左孩子结点存放在 a[2i] 中,右孩子结点存放在 a[2i+1] 中。
若是大顶堆,则有 a[i].key≥a[2i].key 且:
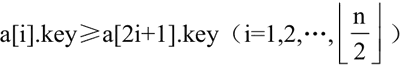
若是小顶堆,则有 a[i].key≤a[2i].key 且:
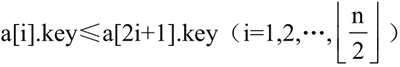
建立一个大顶堆就是将一个无序的关键字序列构建为一个满足条件 a[i]≥a[2i] 与 a[i]≥a[2i+1],其中 i=1,2,...,⌊n/2⌋ 的序列。
建立大顶堆的算法思想:从位于元素序列中的最后一个非叶子结点,即第 ⌊n/2⌋ 个元素开始,逐层比较,直到根结点为止。
假设当前结点的序号为 i,则当前元素为 a[i],其左、右孩子结点元素分别为 a[2i] 和 a[2i+1]。将 a[2i].key 和 a[2i+1].key 较大者与 a[i] 比较,若孩子结点的元素值大于当前结点值,则交换两者,否则不进行交换。
逐层向上执行此操作,直到根结点,这样就建立了一个大顶堆。建立小顶堆的算法与此类似。
例如,给定一组元素,其关键字序列为(21,47,39,51,39,57,48,56),建立大顶堆的过程如下图所示。结点的旁边为对应的序号。
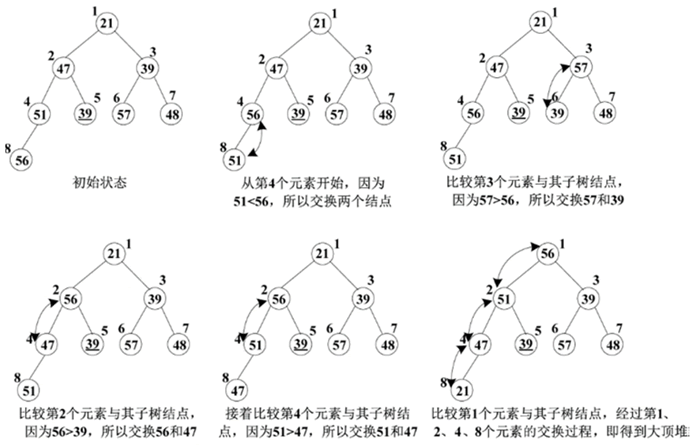
图 5 建立大顶堆的过程
从图 5 可以看出,建立后的大顶堆,其非叶子结点的元素值均不小于左、右子树结点的元素值。
建立大顶堆的算法描述如下:
其实,这也是一个建堆的过程,由于除堆顶元素外,剩下的元素本身就具有 a[i].key≥a[2i].key 且:
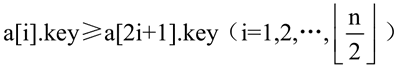
的性质,关键字按照由大到小的顺序逐层排列,因此调整剩下的元素构成新的大顶堆,只需要从上往下进行比较,找出最大的关键字并将其放在根结点的位置,就构成了一个新堆。
具体实现:当堆顶元素输出后,可以将堆顶元素放在堆的最后,即将第 1 个元素与最后一个元素交换,需要调整的元素序列就是 a[1…n-1]。
从根结点开始,若其左、右子树结点的元素值大于根结点的元素值,则选择较大的一个进行交换。也就是说:
重复执行此操作,直到叶子结点不存在,就完成了堆的调整,构成了一个新堆。
例如,一个大顶堆的关键字序列为 (87,64,53,51,23,21,48,32),当输出 87 后,调整剩余的关键字序列为一个新的大顶堆的过程如下图所示:

图 7 输出堆顶元素后,调整堆的过程
重复输出堆顶元素,即将堆顶元素与堆的最后一个元素交换,然后重新调整剩余的元素序列使其构成一个新的大顶堆,直到没有需要输出的元素为止。重复执行以上操作,就会把元素序列调整为一个有序序列,即完成排序的过程。
例如,一个大顶堆的元素的关键字序列为 (87,64,49,51,49,21,48,32),其相应的完整的堆排序过程如下图所示。
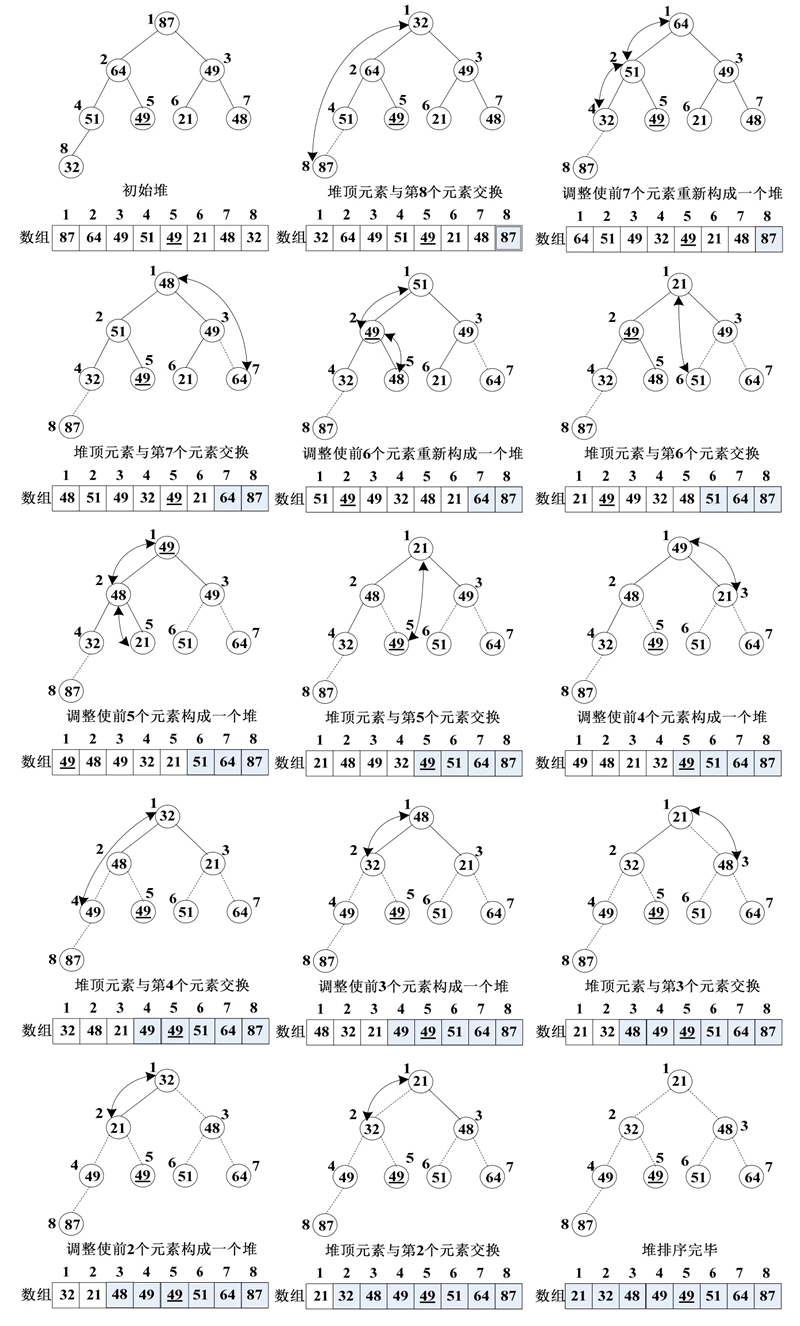
图 8 一个完整的堆排序过程
堆排序是一种不稳定的排序。堆排序的时间主要耗费在建立堆和不断调整堆的过程。堆排序在最坏的情况下时间复杂度为 O(nlog2n)。堆排序适用于待排序的数据量较大的情况。
堆排序是利用二叉树的树形结构,按照完全二叉树的编号次序,将元素序列的关键字依次存放在相应的结点。然后从叶子结点开始,从互为兄弟的两个结点中(没有兄弟结点的除外)选择一个较大(或较小)者与其双亲结点比较,若该结点大于(或小于)双亲结点,则将两者进行交换,使较大(或较小)者成为双亲结点。
对所有的结点都进行类似操作,直到根结点为止。此时,根结点的元素值的关键字最大(或最小)。这样就构成了堆,堆中的每一个结点都大于(或小于)其孩子结点。
堆的数学形式定义为:假设存在 n 个元素,其关键字序列为 (k1,k2,…,ki,…,kn),如果有:
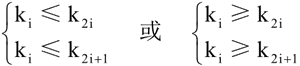
其中 i=1,2,...,⌊n/2⌋,称此元素序列构成了一个堆。
若将这些元素的关键字存放在数组中,将此数组中的元素与完全二叉树一一对应起来,则完全二叉树中的每个非叶子结点的值都不小于(或不大于)孩子结点的值。
在堆中,堆的根结点元素值一定是所有结点元素值的最大值或最小值。例如,序列 (87,64,53,51,23,21,48,32) 和 (12,35,27,46,41,39,48,55,89,76)都是堆,相应的完全二叉树表示如下图所示:

图 2 大顶堆和小顶堆
在图 2 中,一个是非叶子结点的元素值不小于其孩子结点的元素值,这样的堆称为大顶堆;另一个是非叶子结点的元素值不大于其孩子结点的元素值,这样的堆称为小顶堆。
若将堆中的根结点(堆顶)输出之后,将剩余的 n-1 个结点的元素值重新建立一个堆,则新堆的堆顶元素值是次大(或次小)值,将该堆顶元素输出。然后将剩余的 n-2 个结点的元素值重新建立一个堆,反复执行以上操作,直到堆中没有结点,就构成了一个有序序列,这样的重复建堆并输出堆顶元素的过程称为堆排序。
堆的建立
堆排序的过程就是建立堆和不断调整使剩余结点构成新堆的过程。假设将待排序的元素的关键字存放在数组 a 中,第 1 个元素的关键字 a[1] 表示二叉树的根结点,剩下的元素的关键字 a[2…n] 分别与二叉树中的结点按照层次从左到右一一对应。
例如,根结点的左孩子结点存放在 a[2] 中,右孩子结点存放在 a[3] 中,a[i] 的左孩子结点存放在 a[2i] 中,右孩子结点存放在 a[2i+1] 中。
若是大顶堆,则有 a[i].key≥a[2i].key 且:
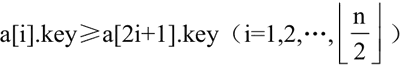
若是小顶堆,则有 a[i].key≤a[2i].key 且:
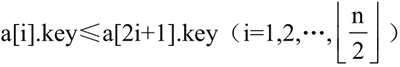
建立一个大顶堆就是将一个无序的关键字序列构建为一个满足条件 a[i]≥a[2i] 与 a[i]≥a[2i+1],其中 i=1,2,...,⌊n/2⌋ 的序列。
建立大顶堆的算法思想:从位于元素序列中的最后一个非叶子结点,即第 ⌊n/2⌋ 个元素开始,逐层比较,直到根结点为止。
假设当前结点的序号为 i,则当前元素为 a[i],其左、右孩子结点元素分别为 a[2i] 和 a[2i+1]。将 a[2i].key 和 a[2i+1].key 较大者与 a[i] 比较,若孩子结点的元素值大于当前结点值,则交换两者,否则不进行交换。
逐层向上执行此操作,直到根结点,这样就建立了一个大顶堆。建立小顶堆的算法与此类似。
例如,给定一组元素,其关键字序列为(21,47,39,51,39,57,48,56),建立大顶堆的过程如下图所示。结点的旁边为对应的序号。

图 5 建立大顶堆的过程
从图 5 可以看出,建立后的大顶堆,其非叶子结点的元素值均不小于左、右子树结点的元素值。
建立大顶堆的算法描述如下:
public void CreateHeap(int n)
// 建立大顶堆
{
for(int i=n/2-1; i>=0; i--) // 从序号 n/2 开始建立大顶堆
AdjustHeap(i, n-1);
}
public void AdjustHeap(int s, int m)
// 调整 H.data[s...m] 的关键字,使其成为一个大顶堆
{
int t = data[s]; // 将根结点暂时保存在 t 中
int j=2*s+1;
while(j<=m) {
if (j < m && data[j] < data[j + 1]) // 沿关键字较大的孩子结点向下筛选
j++;
if (t > data[j]) // 若孩子结点的值小于根结点的值,则不进行交换
break;
data[s] = data[j];
s = j;
j *= 2 + 1;
}
data[s] = t; // 将根结点插入正确位置
}
调整堆
建立一个大顶堆后,当输出堆顶元素后,如何调整剩下的元素,使其构成一个新的大顶堆呢?其实,这也是一个建堆的过程,由于除堆顶元素外,剩下的元素本身就具有 a[i].key≥a[2i].key 且:
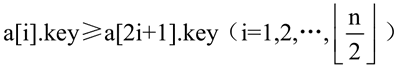
的性质,关键字按照由大到小的顺序逐层排列,因此调整剩下的元素构成新的大顶堆,只需要从上往下进行比较,找出最大的关键字并将其放在根结点的位置,就构成了一个新堆。
具体实现:当堆顶元素输出后,可以将堆顶元素放在堆的最后,即将第 1 个元素与最后一个元素交换,需要调整的元素序列就是 a[1…n-1]。
从根结点开始,若其左、右子树结点的元素值大于根结点的元素值,则选择较大的一个进行交换。也就是说:
- 若 a[2]>a[3],则将 a[1] 与 a[2] 进行比较,若 a[1]>a[2],则将 a[1] 与 a[2] 交换,否则不交换;
- 若 a[2]<a[3],则将 a[1] 与 a[3] 进行比较,若 a[1]>a[3],则将 a[1] 与 a[3]交换,否则不交换。
重复执行此操作,直到叶子结点不存在,就完成了堆的调整,构成了一个新堆。
例如,一个大顶堆的关键字序列为 (87,64,53,51,23,21,48,32),当输出 87 后,调整剩余的关键字序列为一个新的大顶堆的过程如下图所示:

图 7 输出堆顶元素后,调整堆的过程
重复输出堆顶元素,即将堆顶元素与堆的最后一个元素交换,然后重新调整剩余的元素序列使其构成一个新的大顶堆,直到没有需要输出的元素为止。重复执行以上操作,就会把元素序列调整为一个有序序列,即完成排序的过程。
public void HeapSort()
// 对顺序表 H 进行堆排序
{
CreateHeap(length); // 创建堆
for(int i=length-1; i>0; i--) // 将堆顶元素与最后一个元素交换,重新调整堆
{
int t = data[0];
data[0] = data[i];
data[i] = t;
AdjustHeap(0, i - 1); // 将 data[1~i - 1] 调整为大顶堆
}
}
例如,一个大顶堆的元素的关键字序列为 (87,64,49,51,49,21,48,32),其相应的完整的堆排序过程如下图所示。

图 8 一个完整的堆排序过程
堆排序是一种不稳定的排序。堆排序的时间主要耗费在建立堆和不断调整堆的过程。堆排序在最坏的情况下时间复杂度为 O(nlog2n)。堆排序适用于待排序的数据量较大的情况。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: