快速排序算法(图文并茂,C++实现)
在生活中到处都会用到排序算法,例如比赛、奖学金评选、推荐系统等。排序算法有很多种,能不能找到更快速、高效的排序算法呢?
有人通过实验对各种排序算法做了对比(单位:毫秒),对比结果如下表所示。
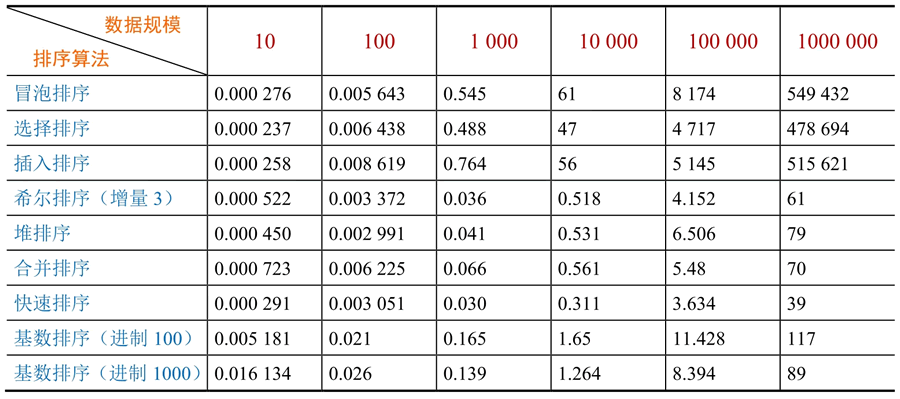
从上表可以看出,若对 10 万个数据进行排序,则采用冒泡排序需要 8174 毫秒,采用快速排序只需 3.634 毫秒!
快速排序是比较快速的排序算法,它的基本思想:首先通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据小,然后按此方法对这两部分数据分别进行快速排序,最终得到有序序列。
和合并排序一样,快速排序算法也是遵循分治策略实现的。合并排序的划分很简单,每次都从中间位置把问题一分为二,一直分解到不能再分解时执行合并操作,但合并操作需要在辅助数组中完成,是一种异地排序算法。合并排序分解容易、合并困难,属于“先易后难”。而快速排序是原地排序,不需要辅助数组,但分解困难、合并容易,属于“先难后易”。
如何分解是一个难题,因为若基准元素选取不当,原序列就有可能被分解为规模为 0 和 n-1 的两个子序列,这样快速排序就退化为冒泡排序了。
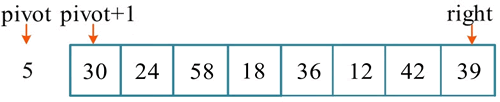
例如,有序列(30,24,5,58,18,36,12,42,39),采用快速排序的分治策略,第 1 次选取 5 作为基准元素,序列被分解后如下图所示。
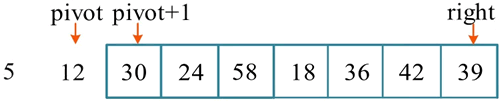
第 2 次选取 12 作为基准元素,序列被分解后如下图所示:
这样做的效率是最低的,最理想的状态是将原序列分解为两个规模相当的子序列,那么怎样选取基准元素呢?一般来说,可通过以下方法选取基准元素:
至此完成一趟排序。此时以 mid 为界,将原序列分解为两个子序列,左侧的子序列都小于或等于 pivot,右侧的子序列都大于或等于 pivot。接着对这两个子序列分别进行快速排序。
下面以序列(30,24,5,58,18,36,12,42,39)为例,演示快速排序的过程。
1) 初始化。i=left,j=right,pivot=r[left]=30。

2) 从右向左扫描,找小于或等于 pivot 的数,找到 a[j]=12。

a[i]=a[j],i++,如下图所示:

3) 从左向右扫描,找大于或等于 pivot 的数,找到 a[i]=58。

a[j]=a[i],j--,如下图所示:

4) 从右向左扫描,找小于或等于 pivot 的数,找到 a[j]=18。

a[i]=a[j],i++,如下图所示:

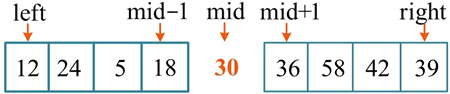
5) 此时 i=j,第一趟排序结束,将 pivot 放到中间,即 a[i]=pivot,返回 i 的位置,mid=i,如下图所示:
此时以 mid 为界,将原序列分解为两个子序列,左侧的子序列都比 pivot 小,右侧的子序列都比 pivot 大。接着分别对两个子序列(12,24,5,18)、(36,58,42,39)进行快速排序。
先从右向左扫描,找小于或等于 pivot 的数,找到后 a[i++]=a[j];再从左向右扫描,找大于或等于 pivot 的数,找到后 a[j--]=a[i]。扫描交替进行,直到 i=j 时停止,将 pivot 放到中间,返回划分的中间位置 i。
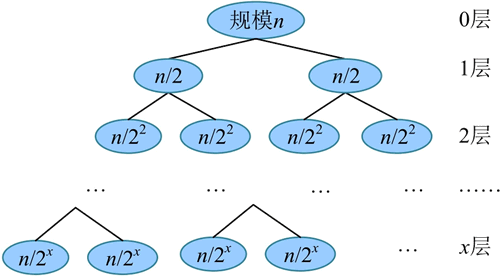
解决子问题:在最好情况下,每次划分都将问题分解为两个规模为 n/2 的子问题,递归求解两个规模为 n/2 的子问题,所需时间为 2T(n/2),如下图所示。

合并:因为是原地排序,所以合并操作不涉及时间复杂度,如下图所示。
总运行时间如下:
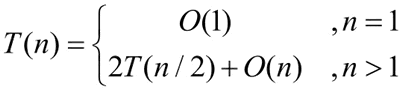
与合并排序的分析方法相同,快速排序在最好情况下的时间复杂度为 O(nlogn)。
空间复杂度:程序中变量的辅助空间是常数阶的,递归调用所使用的栈空间为递归树的高度O(logn),快速排序在最好情况下的空间复杂度为 O(logn)。
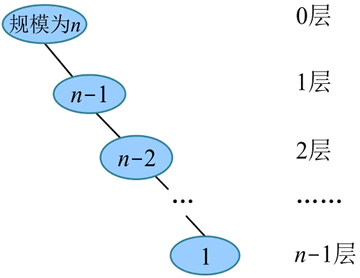
解决子问题:在最坏情况下,在每次划分并将问题分解后,基准元素左侧(或者右侧)都没有元素,基准元素另一侧都为一个规模为 n-1 的子问题,递归求解这个规模为 n-1 的子问题,所需时间为 T(n-1),如下图所示。

合并:因为是原地排序,所以合并操作不涉及时间复杂度,如下图所示:
所以总运行时间如下:
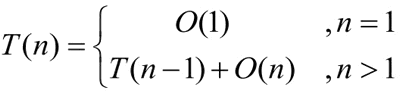
当 n>1 时,可以递推求解:
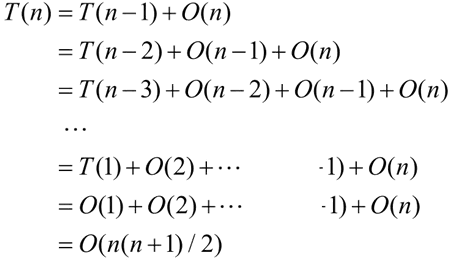
快速排序在最坏情况下的时间复杂度为 O(n^2)。
空间复杂度:程序中变量的辅助空间是常数阶的,递归调用所使用的栈空间为递归树的高度 O(n),快速排序在最坏情况下的空间复杂度为 O(n)。

则:
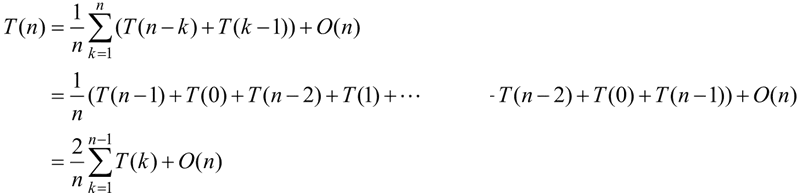
由归纳法可以得出,T(n) 的数量级也为 O(nlogn)。快速排序在平均情况下的时间复杂度为 O(nlogn)。递归调用所使用的栈空间为 O(logn),快速排序在平均情况下的空间复杂度为 O(logn)。
算法代码:
有人通过实验对各种排序算法做了对比(单位:毫秒),对比结果如下表所示。

从上表可以看出,若对 10 万个数据进行排序,则采用冒泡排序需要 8174 毫秒,采用快速排序只需 3.634 毫秒!
快速排序是比较快速的排序算法,它的基本思想:首先通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据小,然后按此方法对这两部分数据分别进行快速排序,最终得到有序序列。
和合并排序一样,快速排序算法也是遵循分治策略实现的。合并排序的划分很简单,每次都从中间位置把问题一分为二,一直分解到不能再分解时执行合并操作,但合并操作需要在辅助数组中完成,是一种异地排序算法。合并排序分解容易、合并困难,属于“先易后难”。而快速排序是原地排序,不需要辅助数组,但分解困难、合并容易,属于“先难后易”。
快速排序算法设计
快速排序算法的思想如下:- 分解:先从原序列中取出一个元素作为基准元素。以基准元素为界,将原序列分解为两个子序列,小于或等于基准元素的子序列在基准元素左侧,大于或等于基准元素的子序列在基准元素右侧;
- 治理:对两个子序列分别进行快速排序;
- 合并:将两个有序子序列合并为一个有序序列,得到原问题的解。
如何分解是一个难题,因为若基准元素选取不当,原序列就有可能被分解为规模为 0 和 n-1 的两个子序列,这样快速排序就退化为冒泡排序了。
例如,有序列(30,24,5,58,18,36,12,42,39),采用快速排序的分治策略,第 1 次选取 5 作为基准元素,序列被分解后如下图所示。

第 2 次选取 12 作为基准元素,序列被分解后如下图所示:

这样做的效率是最低的,最理想的状态是将原序列分解为两个规模相当的子序列,那么怎样选取基准元素呢?一般来说,可通过以下方法选取基准元素:
- 选取第一个元素;
- 选取最后一个元素;
- 选取中间位置的元素;
- 选取第一个元素、最后一个元素、中间位置的元素这三者的中位数;
- 选取区间位置随机数 k(left≤k≤right),选取 a[k] 作为基准元素。
快速排序算法图解
因为不确定通过哪种方法选取基准元素效果最好,在此选取第一个元素作为基准元素。假设当前待排序序列为 a[left:right],其中 left≤right:- 选取数组的第一个元素作为基准元素,pivot=a[left],i=left,j=right;
- 从右向左扫描,找小于或等于 pivot 的数,令 a[i]=a[j],i++;
- 从左向右扫描,找大于或等于 pivot 的数,令 a[j]=a[i],j--;
- 重复第 2~3 步,直到 i 和 j 重合,将 pivot 放到中间,即 a[i]=pivot,返回 mid=i。
至此完成一趟排序。此时以 mid 为界,将原序列分解为两个子序列,左侧的子序列都小于或等于 pivot,右侧的子序列都大于或等于 pivot。接着对这两个子序列分别进行快速排序。
下面以序列(30,24,5,58,18,36,12,42,39)为例,演示快速排序的过程。
1) 初始化。i=left,j=right,pivot=r[left]=30。

2) 从右向左扫描,找小于或等于 pivot 的数,找到 a[j]=12。

a[i]=a[j],i++,如下图所示:

3) 从左向右扫描,找大于或等于 pivot 的数,找到 a[i]=58。

a[j]=a[i],j--,如下图所示:

4) 从右向左扫描,找小于或等于 pivot 的数,找到 a[j]=18。

a[i]=a[j],i++,如下图所示:

5) 此时 i=j,第一趟排序结束,将 pivot 放到中间,即 a[i]=pivot,返回 i 的位置,mid=i,如下图所示:

此时以 mid 为界,将原序列分解为两个子序列,左侧的子序列都比 pivot 小,右侧的子序列都比 pivot 大。接着分别对两个子序列(12,24,5,18)、(36,58,42,39)进行快速排序。
快速排序算法实现
1) 划分函数
通过划分函数,以基准元素 pivot 为界,将原序列分解为两个子序列:- 小于或等于 pivot 的子序列在 pivot 左侧;
- 大于或等于 pivot 的子序列在 pivot 右侧。
先从右向左扫描,找小于或等于 pivot 的数,找到后 a[i++]=a[j];再从左向右扫描,找大于或等于 pivot 的数,找到后 a[j--]=a[i]。扫描交替进行,直到 i=j 时停止,将 pivot 放到中间,返回划分的中间位置 i。
int partition(int left, int right) { // 划分函数
int i = left, j = right, pivot = a[left]; // 选取第一个元素作为基准元素
while (i < j) {
while (a[j] > pivot && i < j) j--; // 找右侧小于或等于 pivot 的数
if (i < j)
a[i++] = a[j]; // 覆盖
while (a[i] < pivot && i < j) i++; // 找左侧大于或等于 pivot 的数
if (i < j)
a[j--] = a[i]; // 覆盖
}
a[i] = pivot; // 把 pivot 放到中间
return i;
}
2) 快速排序
首先对原序列进行划分,得到划分的中间位置 mid。然后以中间位置为界,分别对左半部分(left,mid-1)进行快速排序,对右半部分(mid+1,right)进行快速排序。递归结束的条件是 left≥right。
void quicksort(int left, int right) { // 快速排序
if (left < right) {
int mid = partition(left, right); // 划分
quicksort(left, mid - 1); // 将左侧的子序列快速排序
quicksort(mid + 1, right); // 将右侧的子序列快速排序
}
}
快速排序算法分析
下面将快速排序分为最好情况、最坏情况和平均情况进行算法分析。1) 最好情况
分解:划分函数需要扫描每个元素,每次扫描的元素数量都不超过 n,因此时间复杂度为 O(n)。解决子问题:在最好情况下,每次划分都将问题分解为两个规模为 n/2 的子问题,递归求解两个规模为 n/2 的子问题,所需时间为 2T(n/2),如下图所示。

合并:因为是原地排序,所以合并操作不涉及时间复杂度,如下图所示。

总运行时间如下:
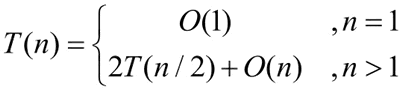
与合并排序的分析方法相同,快速排序在最好情况下的时间复杂度为 O(nlogn)。
空间复杂度:程序中变量的辅助空间是常数阶的,递归调用所使用的栈空间为递归树的高度O(logn),快速排序在最好情况下的空间复杂度为 O(logn)。
2) 最坏情况
分解:划分函数需要扫描每个元素,每次扫描的元素数量都不超过 n,因此时间复杂度为 O(n)。解决子问题:在最坏情况下,在每次划分并将问题分解后,基准元素左侧(或者右侧)都没有元素,基准元素另一侧都为一个规模为 n-1 的子问题,递归求解这个规模为 n-1 的子问题,所需时间为 T(n-1),如下图所示。

合并:因为是原地排序,所以合并操作不涉及时间复杂度,如下图所示:

所以总运行时间如下:
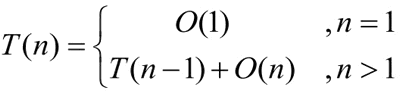
当 n>1 时,可以递推求解:
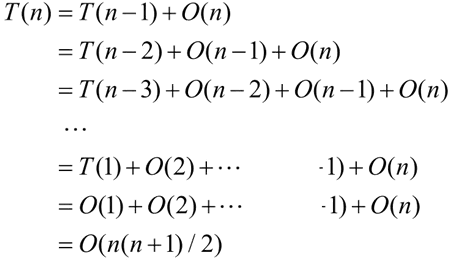
快速排序在最坏情况下的时间复杂度为 O(n^2)。
空间复杂度:程序中变量的辅助空间是常数阶的,递归调用所使用的栈空间为递归树的高度 O(n),快速排序在最坏情况下的空间复杂度为 O(n)。
3) 平均情况
假设划分后的基准元素在第 k(k=1,2,…,n)个位置,如下图所示:
则:
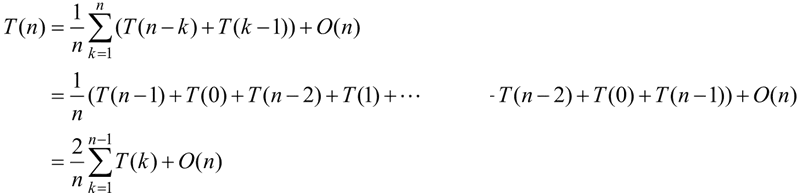
由归纳法可以得出,T(n) 的数量级也为 O(nlogn)。快速排序在平均情况下的时间复杂度为 O(nlogn)。递归调用所使用的栈空间为 O(logn),快速排序在平均情况下的空间复杂度为 O(logn)。
快速排序优化拓展
为避免出现最坏情况,可以在选取基准元素时引入随机化策略,首先生成一个 [left,right] 区间的随机数 k,然后将 a[k] 和 a[left] 交换,其他代码保持不变。算法代码:
int partition2(int left, int right) { // 划分函数,引入随机化策略
int k = left + rand() % (right - left + 1); // 生成 [left, right] 区间的随机数
swap(a[k], a[left]);
int i = left, j = right, pivot = a[left];
while (i < j) {
while (a[j] > pivot && i < j) j--; // 找右侧小于或等于 pivot 的数
if (i < j)
a[i++] = a[j]; // 覆盖
while (a[i] < pivot && i < j) i++; // 找左侧大于或等于 pivot 的数
if (i < j)
a[j--] = a[i]; // 覆盖
}
a[i] = pivot; // 放到中间
return i;
}
注意:
- 选取基准元素时应尽量引入随机化策略。选取第一个元素或最后一个元素作为基准元素时,若序列本身有序,则会退化为最坏情况,出现超时的情况;
- 在划分函数中,与 pivot 比较的语句不要带等号。若该语句带有等号,例如 while(a[j]>=pivot&&i<j),当序列元素均等时,则会退化为最坏情况,出现超时的情况。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: