梯度下降求极值
在《线性回归:损失函数和假设函数》一节,从数学的角度解释了假设函数和损失函数,我们最终的目的要得到一个最佳的“拟合”直线,因此就需要将损失函数的偏差值减到最小,我们把寻找极小值的过程称为“优化方法”,常用的优化方法有很多,比如共轭梯度法、梯度下降法、牛顿法和拟牛顿法。你可能对于上述方法感到陌生,甚至于害怕,其实大可不必,它们只不过应用了一些数学公式而已。
本节我们重点学习梯度下降法(Gradient Descent),在认识该方法之前,我们先复习一下高中时的数学知识。
导数有其严格的数学定义,它巧妙的利用了极限的思想,也就是无限趋近于 0 的思想。设函数 y=f(x) 在点 x0 的某个邻域内有定义,当自变量 x 在 x0 处有增量 Δx,(x0+Δx)也在该邻域内时,相应地函数取得增量 Δy=f(x0+Δx)-f(x0);如果 Δy 与 Δx 之比当 Δx→0 时极限存在,则称函数 y=f(x) 在点 x0 处可导,并称这个极限为函数 y=f(x) 在点 x0 处的导数记做 :
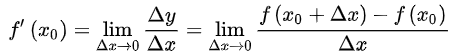
那么什么样的函数具有导数呢?是不是所有的函数都有导数?当然不是,而且函数也不一定在其所有点上都有导数。如果某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。可导的函数一定连续;不连续的函数一定不可导。
导数的发明者是伟大的科学家牛顿与布莱尼茨,它是微积分的一个重要的支柱。在机器学习中,我们只需会用前辈科学家们留下来的知识就行了,比如熟悉常见的导函数公式,以下列举了常用的导数公式:
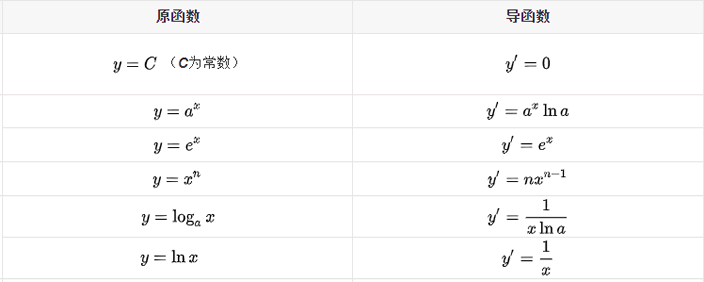
有如下函数 z = x2 + 3xy + y2,分别求 z 对于 x 、y 的偏导数。如下所示:
梯度是微积分学的术语,它本质上是一个向量,表示函数在某一点处的方向导数上沿着特定的方向取得最大值,即函数在该点处沿着该方向变化最快,变化率最大。梯度下降法的计算过程就是沿梯度方向求解极小值,当然你也可以沿梯度上升的方向求解极大值。
那么如何能够更好的理解“梯度下降”呢?如果不考虑其他外在因素,其实你可以把它想象成“下山”的场景,如何从一个高山上以最快的时间走到山脚下呢?其实很简单,以你所在的当前位置为基准,寻找该位置最陡峭的地方,然后沿着此方向向下走,并且每走一段距离,都要寻找当前位置“最陡峭的地方”,反复采用上述方法,最终就能以最快的时间抵达山脚下。
在这个下山的过程中,“寻找所处位置最陡峭的地方,并沿此位置向下走”最为关键,如果把这个做法对应到函数中,就是找到“给定点的梯度”而梯度的方向就是函数值变化最快的方向。
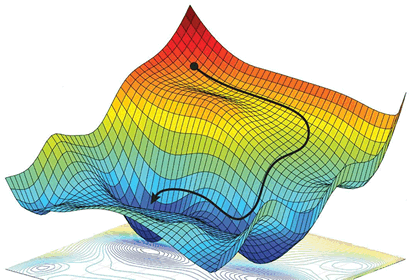
图1:示意图
从上述描述中,你可能感觉到平淡无奇,其实每一个词语都蕴含着数学知识,比如“以当前所在位置为基准,找到最陡峭的地方”从数学角度来讲就是找到所在点的“切线”方向,也就是对这点“求导”,然后循着切线轨迹点反复使用此方法,就可以到达极小值点。
在《线性回归:损失函数和假设函数》一节,我们讲解了线性回归的损失函数,而梯度下降作为一种优化方法,其目的是要使得损失值最小。因此“梯度下降”就需要控制损失函数的
“学习率”是一个由外部输入的参数,被称为“超参数”,可以形象地把它理解为下山时走的“步长”大小,想要 w 多调整一点,就把学习率调高一点。不过学习率也不是越高越好,过高的学习率可能导致调整幅度过大,导致无法求得真正的最小值。当损失函数取得极小值时,此时的参数值被称为“最优参数”。因此,在机器学习中最重要的一点就是寻找“最优参数”。
梯度下降是个大家族,它有很多成员,比如批量梯度下降(BGD)、随机梯度下降(SGD)、小批量梯度下降(MBGD),其中批量梯度下降是最常用的,相关内容后续会详细介绍。
本节我们重点学习梯度下降法(Gradient Descent),在认识该方法之前,我们先复习一下高中时的数学知识。
导数
导数也叫导函数,或者微商,它是微积分中的重要基础概念,从物理学角度来看,导数是研究物体某一时刻的瞬时速度,比如你开车从家 8:00 出发到公司上班,9:00 到到达公司,这一个小时内的平均车速是 80km/h,而途中8:15:30这一时刻的速度,就被称为瞬时速度,此刻的速度可能是 100km/h,也可能是 20km/h。而从几何意义上来讲,你可以把它理解为该函数曲线在一点上的切线斜率。导数有其严格的数学定义,它巧妙的利用了极限的思想,也就是无限趋近于 0 的思想。设函数 y=f(x) 在点 x0 的某个邻域内有定义,当自变量 x 在 x0 处有增量 Δx,(x0+Δx)也在该邻域内时,相应地函数取得增量 Δy=f(x0+Δx)-f(x0);如果 Δy 与 Δx 之比当 Δx→0 时极限存在,则称函数 y=f(x) 在点 x0 处可导,并称这个极限为函数 y=f(x) 在点 x0 处的导数记做 :
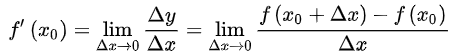
那么什么样的函数具有导数呢?是不是所有的函数都有导数?当然不是,而且函数也不一定在其所有点上都有导数。如果某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。可导的函数一定连续;不连续的函数一定不可导。
导数的发明者是伟大的科学家牛顿与布莱尼茨,它是微积分的一个重要的支柱。在机器学习中,我们只需会用前辈科学家们留下来的知识就行了,比如熟悉常见的导函数公式,以下列举了常用的导数公式:

关于导数的的推断过程详细可参见百度百科。
偏导数
偏导数虽然和导数只有一字之差,但是却相差甚多,从它们的定义来看,偏导数是指对含有两个自变量的函数中的一个自变量求导,也就是说偏导数要求函数必须具备两个自变量。比如拿 z=f(x,y) 举例,如果只有自变量x变化,而自变量y固定(即看作常量),这时它就是x的一元函数,这函数对x的导数,就称为二元函数z对于x的偏导数,记做 fx(x,y) 。有如下函数 z = x2 + 3xy + y2,分别求 z 对于 x 、y 的偏导数。如下所示:
fx(x,y) = 2x + 3y # 关于 x 的偏导数 fy(x,y) = 3x + 2y # 关于 y 的偏导数当求 x 的偏导时就要把 y 当做常数项来对待,而当求 y 的偏导时就要把 x 当做常数项对待。关于偏导数还会涉及到高阶偏,如果感兴趣的话可以点击了解一下。
梯度下降
梯度下降是机器学习中常用的一种优化方法,主要用来解决求极小值的问题,某个函数在某点的梯度指向该函数取得最大值的方向,那么它的反反向自然就是取得最小值的方向。在解决线性回归和 Logistic(逻辑) 回归问题时,梯度下降方法有着广泛的应用。梯度是微积分学的术语,它本质上是一个向量,表示函数在某一点处的方向导数上沿着特定的方向取得最大值,即函数在该点处沿着该方向变化最快,变化率最大。梯度下降法的计算过程就是沿梯度方向求解极小值,当然你也可以沿梯度上升的方向求解极大值。
那么如何能够更好的理解“梯度下降”呢?如果不考虑其他外在因素,其实你可以把它想象成“下山”的场景,如何从一个高山上以最快的时间走到山脚下呢?其实很简单,以你所在的当前位置为基准,寻找该位置最陡峭的地方,然后沿着此方向向下走,并且每走一段距离,都要寻找当前位置“最陡峭的地方”,反复采用上述方法,最终就能以最快的时间抵达山脚下。
在这个下山的过程中,“寻找所处位置最陡峭的地方,并沿此位置向下走”最为关键,如果把这个做法对应到函数中,就是找到“给定点的梯度”而梯度的方向就是函数值变化最快的方向。

图1:示意图
从上述描述中,你可能感觉到平淡无奇,其实每一个词语都蕴含着数学知识,比如“以当前所在位置为基准,找到最陡峭的地方”从数学角度来讲就是找到所在点的“切线”方向,也就是对这点“求导”,然后循着切线轨迹点反复使用此方法,就可以到达极小值点。
在《线性回归:损失函数和假设函数》一节,我们讲解了线性回归的损失函数,而梯度下降作为一种优化方法,其目的是要使得损失值最小。因此“梯度下降”就需要控制损失函数的
w和b参数来找到最小值。比如控制 w 就会得到如下方法:
w新=w旧 - 学习率 * 损失值
通过梯度下降计算极小值时,需要对损失函数的w求偏导求得,这个偏导也就是“梯度”,通过损失值来调节w,不断缩小损失值直到最小,这也正是梯度下降的得名来由。“学习率”是一个由外部输入的参数,被称为“超参数”,可以形象地把它理解为下山时走的“步长”大小,想要 w 多调整一点,就把学习率调高一点。不过学习率也不是越高越好,过高的学习率可能导致调整幅度过大,导致无法求得真正的最小值。当损失函数取得极小值时,此时的参数值被称为“最优参数”。因此,在机器学习中最重要的一点就是寻找“最优参数”。
梯度下降是个大家族,它有很多成员,比如批量梯度下降(BGD)、随机梯度下降(SGD)、小批量梯度下降(MBGD),其中批量梯度下降是最常用的,相关内容后续会详细介绍。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: