Python LinearRegression()实现最小二乘法回归(附带实例)
在 Python 中,无须理会烦琐的线性回归求解过程,直接使用 Scikit-Learn 的 linear_model 模块就可以实现线性回归分析。linear_model 模块提供了很多线性模型,包括最小二乘法回归、岭回归、Lasso、贝叶斯回归等。
首先导入 linear_model 模块,程序代码如下:
线性回归是数据挖掘中的基础算法之一,线性回归的思想其实就是解一组方程,得到回归系数,不过在出现误差项之后,方程的解法就发生了改变,一般使用最小二乘法进行计算。
所谓“二乘”,就是平方的意思,最小二乘法也称最小平方和,其目的是通过最小化误差的平方和,使得预测值与真实值无限接近。
linear_model 模块的 LinearRegression() 函数用于实现最小二乘法回归。LinearRegression() 函数拟合一个带有回归系数的线性模型,使得预测值和真实值之间的残差平方和最小,与真实值无限接近。
LinearRegression() 函数语法格式如下:
主要属性:
主要方法:
LinearRegression() 函数调用 fit 属性来拟合数组 X、y,并且将线性模型的回归系数存储在其成员变量 coef_ 属性中。
【实例】假设某地房屋楼层、面积和单价的关系如下图所示:
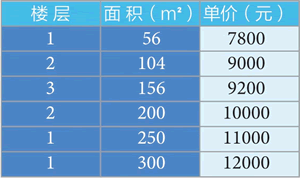
图 1 房屋楼层、面积、单价关系
下面使用 LinearRegression() 函数预测 2 楼面积为 170 平方米的房屋单价。
首先导入 linear_model 模块,程序代码如下:
from sklearn import linear_model导入 linear_model 模块后,在程序中就可以使用相关函数实现线性回归分析了。
线性回归是数据挖掘中的基础算法之一,线性回归的思想其实就是解一组方程,得到回归系数,不过在出现误差项之后,方程的解法就发生了改变,一般使用最小二乘法进行计算。
所谓“二乘”,就是平方的意思,最小二乘法也称最小平方和,其目的是通过最小化误差的平方和,使得预测值与真实值无限接近。
linear_model 模块的 LinearRegression() 函数用于实现最小二乘法回归。LinearRegression() 函数拟合一个带有回归系数的线性模型,使得预测值和真实值之间的残差平方和最小,与真实值无限接近。
LinearRegression() 函数语法格式如下:
linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)参数说明:
- fit_intercept:布尔值,指明是否需要计算截距,默认值为 True。
- normalize:布尔值,指明是否需要标准化,默认值为 False,和参数 fit_intercept 有关。当 fit_intercept 参数值为 False 时,将忽略该参数;当 fit_intercept 参数值为 True 时,则回归前对回归量 X 进行归一化处理,取均值相减,再除以 L2 范数。
- copy_X:布尔值,指明是否复制X数据,默认值为 True,如果为 False,则覆盖 X 数据。
- n_jobs:整型,代表 CPU 工作效率的核数,默认值为 1,-1 表示与 CPU 核数一致。
主要属性:
- coef_:数组或形状,表示线性回归分析的回归系数。
- intercept_:数组,表示截距。
主要方法:
- fit(X, y, sample_weight=None):拟合线性模型;
- predict(X):使用线性模型返回预测值;
- score(X, y, sample_weight=None):返回预测的确定系数 R^2。
LinearRegression() 函数调用 fit 属性来拟合数组 X、y,并且将线性模型的回归系数存储在其成员变量 coef_ 属性中。
【实例】假设某地房屋楼层、面积和单价的关系如下图所示:

图 1 房屋楼层、面积、单价关系
下面使用 LinearRegression() 函数预测 2 楼面积为 170 平方米的房屋单价。
# 导入相关模块
from sklearn import linear_model
import numpy as np
# 创建数据
x = np.array([[1, 56], [2, 104], [3, 156], [2, 200], [1, 250], [1, 300]])
y = np.array([7800, 9000, 9200, 10000, 11000, 12000])
clf = linear_model.LinearRegression() # 创建模型
clf.fit(x, y) # 拟合线性模型
k = clf.coef_ # 回归系数
b = clf.intercept_ # 截距
x0 = np.array([[2, 170]]) # 新数据
# 通过给定的 x0 预测 y0,y0 = 截距 + x0 × 回归系数
y0 = clf.predict(x0) # 预测值
print("回归系数:", k)
print("截距:", b)
print("预测值:", y0)
运行程序,结果如下:
回归系数:[-124.53522378 16.03749212]
截距:7191.56427294429
预测值:[9668.86748582]
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: