C++广度优先搜索算法详解(附带示例)
广度优先搜索是一种基础且重要的算法,通过逐层向外拓展的方式进行搜索,适用于解决等权最短路径或最小操作次数等问题,广泛应用于各种搜索场景。
在广度优先搜索过程中,该算法使用队列记录待拓展的结点。每一步从队列头部(即队伍前端)取出一个结点作为当前拓展点,确保搜索过程按照“逐层推进”的顺序进行。
下图展示了广度优先搜索的顺序:
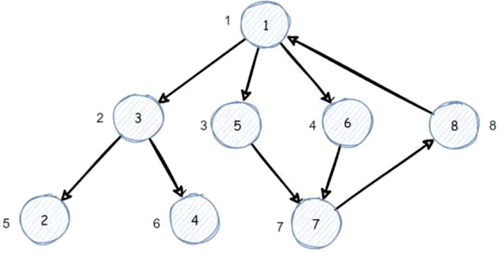
图 1 广度优先搜索示意图
实施广度优先搜索(BFS)时,需要准备一个队列 q 来存储待拓展的顶点,同时使用一个布尔数组(也可以用 bitset 替代)来标记某个顶点是否已被探索(即该顶点已被处理过,后续再次到达此顶点时无须重复处理),并使用一个数组 d 来记录从起点到各顶点的最短距离。
每次拓展的流程如下:
【实例 1】给定一个具有 n 个点、m 条边的有向图,边的权重均为 1,求从点 1 到点 n 的最短距离。可能存在重边与自环。
输入格式:
本题有多组测试样例。第一行包含一个整数 T,表示测试用例的数量(1≤T≤10)。
对于每组测试用例:
输出格式:
对于每组测试用例,输出一个整数表示答案,若不存在从 1 到 n 的路径,则输出 −1。
样例输入:
样例输出
解题思路:本题为广度优先搜索(BFS)模板题,按照 BFS 算法流程编写即可。
【实例 2】小e走迷宫。给定一个大小为 n×m 的矩阵,表示一个迷宫,在矩阵中:
最初,小 e 位于迷宫的左上角 (1,1) 处,每秒钟他可以向上、左、下、右任意一个方向移动一个位置。
现在他想走到迷宫的右下角 (n,m) 处。请你判断他能否到达目的地,若能到达,所需的最短时间是多少呢?
输入格式:
输出格式:
若无法到达 (n,m),则输出 −1;否则,输出所需的最短时间。
样例输入:
样例输出:
本题是经典的广度优先搜索(BFS)例题。从起点出发,搜索每个方向的邻接点,利用 vis 数组标记已访问的点,BFS 算法“一层一层往外走”的特性可以保证搜索到的路径是最短的。
在广度优先搜索过程中,该算法使用队列记录待拓展的结点。每一步从队列头部(即队伍前端)取出一个结点作为当前拓展点,确保搜索过程按照“逐层推进”的顺序进行。
下图展示了广度优先搜索的顺序:

图 1 广度优先搜索示意图
等权的最短路径
当图中所有边的权值相同时,广度优先搜索可以用来解决从特定起点到所有其他顶点的最短路径问题,这通常被称为单源最短路径问题。实施广度优先搜索(BFS)时,需要准备一个队列 q 来存储待拓展的顶点,同时使用一个布尔数组(也可以用 bitset 替代)来标记某个顶点是否已被探索(即该顶点已被处理过,后续再次到达此顶点时无须重复处理),并使用一个数组 d 来记录从起点到各顶点的最短距离。
每次拓展的流程如下:
- 从队列中取出队头的顶点 x;
- 遍历顶点 x 的所有邻接点 y;
- 如果顶点 y 未被更新过,则认定边 x→y 为首次访问 y 的边,因此设置 d[y]=d[x]+1,将 y 加入队列,并标记为已更新状态 vis[y]=true。如果最终发现 d[n] 等于无穷大,则表示不存在从起点到顶点 n 的路径。
【实例 1】给定一个具有 n 个点、m 条边的有向图,边的权重均为 1,求从点 1 到点 n 的最短距离。可能存在重边与自环。
输入格式:
本题有多组测试样例。第一行包含一个整数 T,表示测试用例的数量(1≤T≤10)。
对于每组测试用例:
- 一行包含两个整数 n 和 m(1≤n, m≤10^5)。
- 接下来 m 行,每行包含两个整数 x 和 y(1≤x, y≤n),表示存在一条从 x 指向 y 的边。
输出格式:
对于每组测试用例,输出一个整数表示答案,若不存在从 1 到 n 的路径,则输出 −1。
样例输入:
2
3 2
1 2
2 3
5 4
1 3
3 4
1 2
2 4
样例输出
2
-1
解题思路:本题为广度优先搜索(BFS)模板题,按照 BFS 算法流程编写即可。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 9;
// 定义常量 N,表示结点数量的最大值
const ll inf = 2e18;
// 定义无穷大的值
vector<int> g[N];
// 邻接表存储图的信息
ll n, m, d[N];
// n 表示结点数,m 表示边数,d 数组用于存储从起点到每个结点的最短距离
// bfs() 函数:广度优先搜索算法,用于计算从起点 st 到其他所有结点的最短距离
void bfs(int st) {
for (int i = 1; i <= n; ++i)
d[i] = inf; // 初始化所有结点的距离为无穷大
queue<int> q; // 创建一个队列用于存储待处理的结点
bitset<N> vis; // 使用 bitset 记录每个结点是否已经入过队
d[st] = 0; // 起点到自身的距离为 0
q.push(st); // 将起点加入队列
while (q.size()) { // 当队列不为空时循环
int x = q.front(); // 取出队首元素
q.pop(); // 弹出队首元素
for (const auto &y : g[x]){ // 遍历与 x 相邻的所有结点
if (vis[y]) // 如果 y 已经被访问过,则跳过
continue;
d[y] = d[x] + 1; // 更新 y 的距离为 x 的距离加 1
q.push(y); // 将 y 加入队列
vis[y] = true; // 标记 y 已被访问
}
}
}
// solve() 函数:解决一次测试用例,读取输入数据并调用 bfs() 函数计算最短距离
void solve() {
cin >> n >> m; // 读取结点数和边数
for (int i = 1; i <= n; ++i)
g[i].clear(); // 清空邻接表
for (int i = 1; i <= m; ++i) { // 读取边的信息并构建邻接表
int x, y;
cin >> x >> y;
g[x].push_back(y); // 添加一条从 x 到 y 的边
}
bfs(1); // 从结点 1 开始进行广度优先搜索
// 输出从结点 1 到结点 n 的最短距离,如果无法到达,则输出 -1
cout << (d[n] == inf ? -1 : d[n]) << '\n';
}
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 优化输入/输出流性能
int T;
cin >> T; // 读取测试用例的数量
while (T--) // 对每个测试用例进行处理
solve();
return 0;
}
【实例 2】小e走迷宫。给定一个大小为 n×m 的矩阵,表示一个迷宫,在矩阵中:
- 0 表示空白处,可以行走;
- 1 表示障碍物,不可通过。
最初,小 e 位于迷宫的左上角 (1,1) 处,每秒钟他可以向上、左、下、右任意一个方向移动一个位置。
现在他想走到迷宫的右下角 (n,m) 处。请你判断他能否到达目的地,若能到达,所需的最短时间是多少呢?
输入格式:
- 第一行包含两个整数 n 和 m(1≤n, m≤1000),分别表示矩阵的行数和列数。
- 接下来 n 行,每行包含 m 个整数(0 或 1),表示迷宫矩阵。数据保证 (1,1) 和 (n,m) 均为 0。
输出格式:
若无法到达 (n,m),则输出 −1;否则,输出所需的最短时间。
样例输入:
5 5
0 1 0 0 0
0 0 0 1 0
1 1 0 1 0
0 0 1 0 0
1 0 0 1 0
样例输出:
10
本题是经典的广度优先搜索(BFS)例题。从起点出发,搜索每个方向的邻接点,利用 vis 数组标记已访问的点,BFS 算法“一层一层往外走”的特性可以保证搜索到的路径是最短的。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
typedef pair<int, int> PII;
const int N = 1009;
int g[N][N], n, m;
// 定义地图数组 g,以及地图的行数 n 和列数 m
int d[N][N];
// 定义距离数组 d,用于存储每个点到起点的距离
bitset<N> vis[N];
// 定义访问标记数组 vis,用于记录每个点是否被访问过
int dx[] = {0, 0, 1, -1}; // 定义 4 个方向的横坐标偏移量
int dy[] = {1, -1, 0, 0}; // 定义 4 个方向的纵坐标偏移量
// 判断坐标 (x, y) 是否在地图范围内
bool inmp(int x, int y) {
return x >= 1 && x <= n && y >= 1 && y <= m;
}
// 广度优先搜索函数,从起点 (sx, sy) 开始搜索
void bfs(int sx, int sy) {
queue<PII> q;
// 定义一个队列 q,用于存储待访问的点
memset(d, 0, sizeof d);
// 初始化距离数组 d 为 0
vis[sx][sy] = true;
// 标记起点已被访问
q.push({sx, sy});
// 将起点加入队列
while (q.size()) { // 当队列不为空时循环
int x = q.front().first; // 取出队首点的横坐标
int y = q.front().second; // 取出队首点的纵坐标
q.pop(); // 弹出队首点
for (int i = 0; i < 4; ++i) { // 遍历 4 个方向
int nx = x + dx[i], ny = y + dy[i];
// 计算下一个点的坐标
if (inmp(nx, ny) && !g[nx][ny] && !vis[nx][ny]) {
// 如果下一个点在地图范围内、未被访问过且不是障碍物
d[nx][ny] = d[x][y] + 1; // 更新距离数组
q.push({nx, ny}); // 将下一个点加入队列
vis[nx][ny] = true; // 标记下一个点已被访问
}
}
}
}
// 解决问题的函数
void solve() {
cin >> n >> m; // 输入地图的行数和列数
for (int i = 1; i <= n; ++i) // 遍历地图的每一行
for (int j = 1; j <= m; ++j) // 遍历地图的每一列
cin >> g[i][j]; // 输入地图上的障碍物信息
bfs(1, 1); // 从起点 (1, 1) 开始广度优先搜索
if (vis[n][m]) cout << d[n][m] << '\n'; // 如果终点被访问过,则输出最短距离
else cout << -1; // 否则输出 -1,表示无法到达终点
}
// 主函数
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 优化输入/输出流性能
int _ = 1; // 测试用例的数量,这里只处理一个测试用例
while (_--) solve(); // 调用 solve() 函数处理测试用例
return 0;
}
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: