首页 > 编程笔记 > Java笔记 阅读：71

Java用队列实现杨辉三角（解析+完整实现源码）

杨辉三角是一个由数字排列成的三角形数表，一个 8 阶的杨辉三角图形如下图所示。


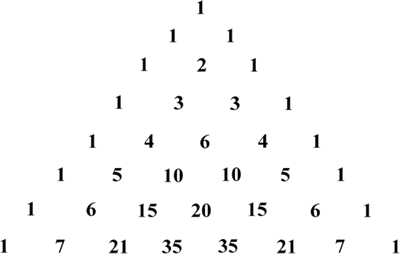
图 1 8 阶的杨辉三角

从上图可以看出，杨辉三角具有以下性质：

队列实现杨辉三角

杨辉三角的第 i 行元素是根据第 i-1 行元素得到的，杨辉三角的形成序列是具有先后顺序的，因此杨辉三角可以通过队列来构造。

可以把杨辉三角分为 2 个部分来构造队列：所有的两端元素 1 作为已知部分，剩下的元素作为要构造的部分。

我们可以通过循环队列来实现杨辉三角的打印，在循环队列中依次存入第 i-1 行元素，再利用第 i-1 行元素得到第 i 行元素，然后依次入队，同时第 i-1 行元素出队并打印输出。

从整体来考虑，利用队列构造杨辉三角的过程，其实就是利用上一层元素序列产生下一层元素序列并入队，然后将上一层元素出队并输出，接着由队列中的元素生成下一层元素，以此类推，直到生成最后一层元素并输出。

我们以第 8 行元素为例来理解杨辉三角的具体构造过程：
1) 在第 8 行中，第一个元素先入队。假设队列为 Q： 
Q.queue[rear]=1
Q.rear=(Q.rear+1)%QUEUESIZE

2) 第 8 行的中间 6 个元素通过第 7 行元素（已经入队）得到并入队： 
Q.queue[rear]=Q.queue[front]+Q.queue[front+1]
Q.rear=(Q.rear+1)% QUEUESIZ
Q.front=(Q.front+1)% QUEUESIZE

3) 第 7 行最后一个元素出队： 
Q.front=(Q.front+1)% QUEUESIZE

4) 第 8 行最后一个元素入队： 
Q.queue[rear]=1
Q.rear=(Q.rear+1)% QUEUESIZE

至此，第 8 行的所有元素都已经入队。其他行的入队操作类似。

杨辉三角队列的实现

打印杨辉三角可以使用顺序队列或链式队列的基本算法实现，也可以直接使用数组模拟队列实现。下面只给出打印杨辉三角的顺序队列实现，使用数组模拟队列实现留给读者自行完成。

【实例】打印杨辉三角。 
public class YangHuiTriangleTest {
    int count;          // 记录输出的行

    public void YangHuiTriangle(int N) throws Exception { // 顺序队列实现打印杨辉三角
        int QUEUESIZE = 20;
        Integer temp[] = new Integer[QUEUESIZE]; // 用于存放每一行的元素
        int k = 0;
        SeqQueue Q = new SeqQueue(); // 初始化顺序队列
        Q.EnQueue(1); // 第一行元素入队
        for (int i = 2; i < N + 1; i++) { // 产生第 i 行元素并入队,同时将第 i-1 行元素保存在临时数组中
            k = 0;
            Q.EnQueue(1); // 第 i 行的第一个元素入队
            for (int j = 1; j < i - 1; j++) { // 利用队列中第 i - 1 行元素产生第 i 行的中间 i - 2 个元素并入队
                Integer t = Q.DeQueue(); // 将第 i - 1 行元素存入临时数组
                temp[k++] = t;
                Integer e = Q.GetHead(); // 取队头元素
                t = t + e; // 利用队列中第 i - 1 行元素产生第 i 行元素
                Q.EnQueue(t);
            }
            Integer t = Q.DeQueue();
            temp[k++] = t; // 将第 i - 1 行的最后一个元素存入临时数组
            PrintArray(temp, k, N); // 第 i 行的最后一个元素入队
            Q.EnQueue(1);
        }
        k = 0;
        while (!Q.IsEmpty()) // 将最后一行元素存入数组之前，要将下标 k 置为 0 // 将最后一行元素存入临时数组
        {
            Integer t = Q.DeQueue();
            temp[k++] = t;
            if (Q.IsEmpty())
                PrintArray(temp, k, N);
        }
    }

    public void PrintArray(Integer a[], int n, int N) // 打印数组中的元素，使其以正确的形式输出
    // 打印数组中的元素，使其以正确的形式输出
    {
        for (int i = 0; i < N - count; i++) // 打印空格
            System.out.print("   ");
        count++;
        for (int i = 0; i < n; i++) // 打印数组中的元素
            System.out.print(a[i] + "   ");
        System.out.println();
    }

    public static void main(String args[]) throws Exception {
        YangHuiTriangleTest Yanghui = new YangHuiTriangleTest();
        System.out.print("请输入要打印的行数: n=");
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        Yanghui.YangHuiTriangle(n);
    }
}
程序运行结果如下： 
请输入要打印的行数: n=5
    1  
   1 1 
  1 2 1
1 3 3 1 
1 4 6 4 1

相关文章