C++ next_permutation()和prev_permutation()函数的用法(附带实例)
在程序设计竞赛中,排列是常见的主题,而 next_permutation() 和 prev_permutation() 函数是处理排列的重要工具。
调用 next_permutation() 函数,可以逐个生成所有可能的排列,该函数接收的参数是数组的起始和结束地址(或迭代器)。该函数的返回值为一个布尔值,若存在下一个排列,则返回 true,并修改原数组为下一个排列;若不存在下一个排列,则返回 false,数组保持不变。
next_permutation() 函数对于解决与排列相关的问题非常有帮助,如旅行商问题、八皇后问题等。需要注意的是,在生成下一个排列时,next_permutation() 函数会修改原始排列,将其变为下一个排列。
与 next_permutation() 函数类似,prev_permutation() 函数在生成上一个排列时会修改数组原来的排列。
【实例 1】假设有一个包含 3 个整数的序列 {3,2,1},要找到这个序列的前一个排列,可以调用 prev_permutation() 函数,示例代码如下:
在这个例子中,循环将生成序列的以下排列:
与 next_permutation() 函数类似,调用 prev_permutation() 函数可以方便地生成序列的所有前一个排列。这在解决排列组合问题、生成全排列等应用场景中非常有用。
同样地,需要包含头文件 <algorithm> 以使用 prev_permutation() 函数。
【实例 2】给定一个数字 n,请按照字典序输出排列 [1,2,…,n] 的全排列。
1) 输入格式:
一个整数 n(1≤n≤10)。
2) 输出格式:
每行输出一个排列,按照字典序从小到大排列。
3) 样例:
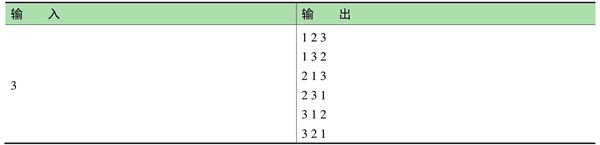
首先初始化字典序最小的排列,然后调用 next_permutation() 函数反复生成下一个排列,直到不存在更多排列为止。
解题思路:首先初始化字典序最小的排列,然后调用 next_permutation() 函数反复生成下一个排列,直到不存在更多排列为止。
C++ next_permutation()函数
next_permutation() 函数的作用是生成给定排列的下一个排列。在算法竞赛中,排列问题经常涉及全排列,即将一组元素按不同的顺序排列。调用 next_permutation() 函数,可以逐个生成所有可能的排列,该函数接收的参数是数组的起始和结束地址(或迭代器)。该函数的返回值为一个布尔值,若存在下一个排列,则返回 true,并修改原数组为下一个排列;若不存在下一个排列,则返回 false,数组保持不变。
next_permutation() 函数对于解决与排列相关的问题非常有帮助,如旅行商问题、八皇后问题等。需要注意的是,在生成下一个排列时,next_permutation() 函数会修改原始排列,将其变为下一个排列。
C++ prev_permutation()函数
prev_permutation() 函数的作用是生成给定排列的上一个排列,在某些问题求解和算法设计中也非常重要。调用 prev_permutation() 函数,可以逐个生成所有可能的上一个排列。与 next_permutation() 函数类似,prev_permutation() 函数在生成上一个排列时会修改数组原来的排列。
【实例 1】假设有一个包含 3 个整数的序列 {3,2,1},要找到这个序列的前一个排列,可以调用 prev_permutation() 函数,示例代码如下:
bool go = true; while (go) { // 在这里可以处理每个生成的排列 go = prev_permutation(sequence.begin(), sequence.end()); }上述循环会依次生成序列的所有前一个排列。在每次迭代中,sequence 会被修改为前一个排列,并返回一个布尔值,表示是否存在前一个排列。
在这个例子中,循环将生成序列的以下排列:
{3,2,1}
{3,1,2}
{2,3,1}
{2,1,3}
{1,3,2}
{1,2,3}
当 prev_permutation() 无法生成前一个排列时,循环将终止。在这个例子中,循环在第 6 次迭代后终止,因为 {1,2,3} 已经是最小的排列。与 next_permutation() 函数类似,调用 prev_permutation() 函数可以方便地生成序列的所有前一个排列。这在解决排列组合问题、生成全排列等应用场景中非常有用。
同样地,需要包含头文件 <algorithm> 以使用 prev_permutation() 函数。
【实例 2】给定一个数字 n,请按照字典序输出排列 [1,2,…,n] 的全排列。
1) 输入格式:
一个整数 n(1≤n≤10)。
2) 输出格式:
每行输出一个排列,按照字典序从小到大排列。
3) 样例:

首先初始化字典序最小的排列,然后调用 next_permutation() 函数反复生成下一个排列,直到不存在更多排列为止。
解题思路:首先初始化字典序最小的排列,然后调用 next_permutation() 函数反复生成下一个排列,直到不存在更多排列为止。
#include <bits/stdc++.h>
using namespace std;
const int N = 12; // 定义常量 N 为 12
int a[N]; // 定义一个长度为 N 的整数数组 a
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 优化输入/输出流的性能
int n; cin >> n; // 从输入流读取一个整数 n
for (int i = 1; i <= n; ++i) a[i] = i; // 初始化数组 a,使其元素值为 1 ~ n
bool go = true; // 定义布尔变量 go,用于控制循环
while (go) { // 当 go 为 true 时执行循环
for (int i = 1; i <= n; ++i)
cout << a[i] << " \n"[i == n]; // 输出数组 a 的元素,并在最后一个元素后换行
go = next_permutation(a + 1, a + 1 + n); // 调用 next_permutation() 函数生成下一个排列,如果存在则返回 true,否则返回 false
}
return 0; // 程序结束
}
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: