C++随机数生成(非常详细)
从游戏到密码学,从抽样到预测,生成随机数对于各种应用程序而言都是很必要的。
但是,“随机数”一词的表述实际上并不正确,因为通过数学公式生成的数字是确定的,不会产生真正的随机数,但数字看起来是随机的,因此叫作伪随机数。
真正的随机性只能通过基于物理过程的硬件设备来实现,即便如此,也可能会受到挑战,因为我们甚至可能认为宇宙实际上也是确定的。现代 C++ 支持通过包含数字生成器和分布的伪随机数库生成伪随机数。理论上来说,它也可以产生真正的随机数,但在实践中那些可能只是伪随机数。
在本节中,我们将讨论标准库对生成伪随机数的支持,其中理解随机数和伪随机数之间的差异是关键:
1) 包含头文件 random:
2) 使用 std::random_device 生成器来初始化伪随机数引擎:
3) 使用其中一个生成数字的引擎,并使用随机种子对其进行初始化:
4) 使用一个可用的分布将引擎的输出转换为所需的统计分布:
5) 生成伪随机数:
所有引擎(除了random_device)产生的整数都服从均匀分布,并且所有引擎都可以实现以下方法:
系统支持以下引擎:
1) linear_congruential_engine:这是一个线性同余生成器。它使用以下公式生成数字:
2) mersenne_twister_engine:这是一个梅森旋转(Mersenne twister)生成器,它在 W (N-1) R 位上保留一个值。每次需要生成一个数字时,它提取 W 位,所有的位都被使用后,它通过移动和混合位来扭曲大的值,以便有一组新的位可来提取。
3) subtract_with_carry_engine:这是一个基于以下公式实现进位减法算法的生成器:
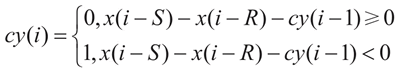
此外,该库还提供了引擎适配器,引擎适配器也是一种引擎,它包裹着其他引擎并且基于基础引擎的输出生成数字。引擎适配器实现了之前提到的基础引擎提供的相同方法。
目前有以下引擎适配器可用:
伪随机数生成器应该根据应用程序的具体要求来选择。线性余同引擎速度中等,但对其内部状态的存储要求非常小;进位减法引擎速度非常快,包括那些没有高级算术指令集处理器机器的引擎,但是它需要更大的存储空间来存储其内部状态,而且生成的数字序列具有较少的理想特性;梅森旋转引擎速度最慢、存储时间最长,但能生成最长的非重复伪随机数序列。
所有这些引擎和引擎适配器都会产生伪随机数。然而,该库提供了另一个名为 random_device 的引擎,该引擎本应该生成不确定的数字,但事实上没有实际的限制,因为随机熵的物理来源可能不可用。因此,random_device 的实现实际上可以基于伪随机数引擎。random_device 类不能像其他引擎那样被种子初始化,它有一个名为 entropy() 的附加方法,该方法返回随机设备熵,对于确定性生成器,它是 0,对于非确定性生成器,它是非零。
然而,这并不是一种确定该设备实际上是确定性的还是非确定性的可靠的方法。例如,GNU libstdc++ 库和 LLVM libc++ 库都实现了一个非确定性设备,但熵返回 0;另外,对于 vc++ 库和 boost.random 库,熵的返回值分别为 32 和 10。
所有这些生成器产生的整数都服从均匀分布,然而,均匀分布只是大多数应用程序中需要的随机数服从的众多统计分布中的一种。为了能够利用其他分布生成数字(整数或实数),该库提供了几个分布类,它们根据引擎实现的统计分布转换引擎的输出。
目前可用的分布如下表所示:
正如前面提到的,库提供的每一个引擎都有优点和缺点。梅森旋转引擎虽然是最慢的,且内部状态最大,但如果进行适当的初始化,可以产生最长的非重复数字序列。在下面的示例中,我们将使用 std::mt19937(内部状态有 19937 位的 32 位梅森旋转引擎)。
生成随机数最简单的方法如下:
初始化引擎有不同的方法,C语言的 random 库的一种常见方法是使用当前时间作为种子。而在现代 C++ 中,它应该是这样的:
std::random_device 类是一个应该返回真正的随机数的引擎,虽然 std::random_device 类的实现确实基于伪随机数生成器,但是它理应返回真正的随机数:

图 2 [1, 6] 内的均匀分布
在本节的最后一个示例中,我们将分布改为均值为 5、标准差为 2 的正态分布。这种分布生成实数,因此为了使用前面的 generate_and_print() 函数,数字必须四舍五入为整数:
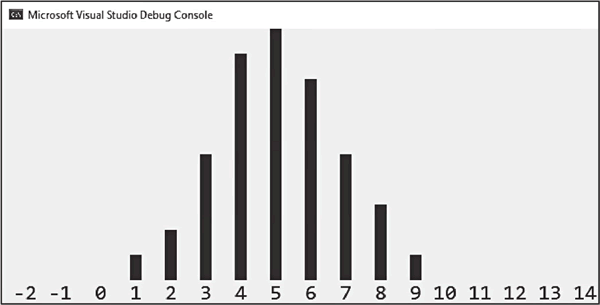
图 3 均值为5、标准差为2的正态分布
如图 3 所示,分布已经从均匀分布变为正态分布(均值为 5)。
但是,“随机数”一词的表述实际上并不正确,因为通过数学公式生成的数字是确定的,不会产生真正的随机数,但数字看起来是随机的,因此叫作伪随机数。
真正的随机性只能通过基于物理过程的硬件设备来实现,即便如此,也可能会受到挑战,因为我们甚至可能认为宇宙实际上也是确定的。现代 C++ 支持通过包含数字生成器和分布的伪随机数库生成伪随机数。理论上来说,它也可以产生真正的随机数,但在实践中那些可能只是伪随机数。
在本节中,我们将讨论标准库对生成伪随机数的支持,其中理解随机数和伪随机数之间的差异是关键:
- 真正的随机数是指不能通过随机过程偶然预测的数字,它是借助硬件随机数生成器生成的;
- 伪随机数是在算法的帮助下生成的数字,这些算法生成的序列具有与真正的随机数近似的特性。
C++随机数生成
要在应用程序中生成伪随机数,应该执行以下步骤:1) 包含头文件 random:
#include <random>
2) 使用 std::random_device 生成器来初始化伪随机数引擎:
std::random_device rd{};
3) 使用其中一个生成数字的引擎,并使用随机种子对其进行初始化:
auto mtgen = std::mt19937{ rd() };
4) 使用一个可用的分布将引擎的输出转换为所需的统计分布:
auto ud = std::uniform_int_distribution<>{ 1, 6 };
5) 生成伪随机数:
for(auto i = 0; i < 20; ++i)
auto number = ud(mtgen);
C++随机数生成的原理
伪随机数库包含两种类型的组件:- 引擎,它们是随机数的生成器,既可以产生服从均匀分布的伪随机数,也可以产生实际随机数(如果有的话)。
- 将引擎的输出转换为统计分布的分布。
所有引擎(除了random_device)产生的整数都服从均匀分布,并且所有引擎都可以实现以下方法:
- min():这是一个静态方法,它返回生成器可以生成的最小值;
- max():这是一个静态方法,它返回生成器可以生成的最大值;
- seed():使用起始值初始化算法(random_device 除外,它无法被种子初始化);
- operator():生成一个均匀分布在 min() 和 max() 之间的新数字;
- discard():生成并丢弃给定数量的伪随机数。
系统支持以下引擎:
1) linear_congruential_engine:这是一个线性同余生成器。它使用以下公式生成数字:
x(i)=(Ax(i-1)+C) mod M
2) mersenne_twister_engine:这是一个梅森旋转(Mersenne twister)生成器,它在 W (N-1) R 位上保留一个值。每次需要生成一个数字时,它提取 W 位,所有的位都被使用后,它通过移动和混合位来扭曲大的值,以便有一组新的位可来提取。
3) subtract_with_carry_engine:这是一个基于以下公式实现进位减法算法的生成器:
x(i)=(x(i-R)-x(i-S)-cy(i-1)) mod M在上式中,cy 定义为:
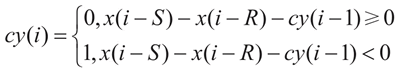
此外,该库还提供了引擎适配器,引擎适配器也是一种引擎,它包裹着其他引擎并且基于基础引擎的输出生成数字。引擎适配器实现了之前提到的基础引擎提供的相同方法。
目前有以下引擎适配器可用:
- discard_block_engine:使基础引擎生成的块(包含 P 个数字)中保留 R 个数字,并丢弃其余的数字的生成器;
- independent_bits_engine:生成与基础引擎不同位数的数字的生成器;
- shuffle_order_engine:该生成器保存一个由基础引擎生成的 K 个数字组成的 shuffle 表,并从该表中返回数字(用基础引擎生成的数字替换它们)。
伪随机数生成器应该根据应用程序的具体要求来选择。线性余同引擎速度中等,但对其内部状态的存储要求非常小;进位减法引擎速度非常快,包括那些没有高级算术指令集处理器机器的引擎,但是它需要更大的存储空间来存储其内部状态,而且生成的数字序列具有较少的理想特性;梅森旋转引擎速度最慢、存储时间最长,但能生成最长的非重复伪随机数序列。
所有这些引擎和引擎适配器都会产生伪随机数。然而,该库提供了另一个名为 random_device 的引擎,该引擎本应该生成不确定的数字,但事实上没有实际的限制,因为随机熵的物理来源可能不可用。因此,random_device 的实现实际上可以基于伪随机数引擎。random_device 类不能像其他引擎那样被种子初始化,它有一个名为 entropy() 的附加方法,该方法返回随机设备熵,对于确定性生成器,它是 0,对于非确定性生成器,它是非零。
然而,这并不是一种确定该设备实际上是确定性的还是非确定性的可靠的方法。例如,GNU libstdc++ 库和 LLVM libc++ 库都实现了一个非确定性设备,但熵返回 0;另外,对于 vc++ 库和 boost.random 库,熵的返回值分别为 32 和 10。
所有这些生成器产生的整数都服从均匀分布,然而,均匀分布只是大多数应用程序中需要的随机数服从的众多统计分布中的一种。为了能够利用其他分布生成数字(整数或实数),该库提供了几个分布类,它们根据引擎实现的统计分布转换引擎的输出。
目前可用的分布如下表所示:
| 类型 | 类名称 | 数值类型 | 统计分布 |
|---|---|---|---|
| 均匀分布 | uniform_int_distribution | 整数 | 均匀分布 |
| uniform_real_distribution | 实数 | 均匀分布 | |
| 伯努利分布 | bernoulli_distribution | 布尔值 | 伯努利分布 |
| binomial_distribution | 整数 | 伯努利分布 | |
| negative_binomial_distribution | 整数 | 负二项分布 | |
| geometric_distribution | 整数 | 几何分布 | |
| 泊松分布 | poisson_distribution | 整数 | 泊松分布 |
| exponential_distribution | 实数 | 指数分布 | |
| gamma_distribution | 实数 | 伽马分布 | |
| weibull_distribution | 实数 | 韦布尔分布 | |
| extreme_value_distribution | 实数 | 极值分布 | |
| normal_distribution | 实数 | 标准正态(高斯) | |
| 正态分布 | lognormal_distribution | 实数 | 对数正态分布 |
| chi_squared_distribution | 实数 | 卡方分布 | |
| cauchy_distribution | 实数 | 柯西分布 | |
| fisher_f_distribution | 实数 | Fisher 的 F 分布 | |
| student_t_distribution | 实数 | 学生 t 分布 | |
| discrete_distribution | Integer | 离散分布 | |
| 抽样 | piecewise_constant_distribution | 实数 | 分布在常数子区间上的值 |
| piecewise_linear_distribution | 实数 | 分布在定义的子区间上的值 |
正如前面提到的,库提供的每一个引擎都有优点和缺点。梅森旋转引擎虽然是最慢的,且内部状态最大,但如果进行适当的初始化,可以产生最长的非重复数字序列。在下面的示例中,我们将使用 std::mt19937(内部状态有 19937 位的 32 位梅森旋转引擎)。
生成随机数最简单的方法如下:
auto mtgen = std::mt19937 {};
for (auto i = 0; i < 10; ++i)
std::cout << mtgen() << '\n';
在这个示例中,mtgen 是梅森旋转引擎 std::mt19937。要生成数字,只需要使用调用操作符来迭代内部状态并返回下一个伪随机数。然而,这段代码是有缺陷的,因为引擎无法用种子初始化。所以,它总是产生相同的数字序列,在大多数情况下这可能不是你想要的。初始化引擎有不同的方法,C语言的 random 库的一种常见方法是使用当前时间作为种子。而在现代 C++ 中,它应该是这样的:
auto seed = std::chrono::high_resolution_clock::now()
.time_since_epoch()
.count();
auto mtgen = std::mt19937{ static_cast<unsigned int>(seed) };
在这个示例中,seed 表示从时钟的纪元到当前时刻的 tick 数,用作初始化引擎的种子。这种方法的问题是,seed 的值实际上是确定的,而且在某些类型的应用程序中,它可能很容易受到攻击。一种更可靠的方法是用实际随机数作为生成器的种子。std::random_device 类是一个应该返回真正的随机数的引擎,虽然 std::random_device 类的实现确实基于伪随机数生成器,但是它理应返回真正的随机数:
std::random_device rd;
auto mtgen = std::mt19937 {rd()};
所有引擎产生的数字都服从均匀分布。为了将结果转换为另一个统计分布,我们必须使用分布类。为了显示生成的数字是如何依据所选定的分布来分布的,我们将使用以下函数。这个函数生成了指定数量的伪随机数,并且计算它们在 map 中的重复次数,然后用 map 的值生成柱状图,以展示每个数字出现的频率:
void generate_and_print(std::function<int(void)> gen,
int const iterations = 10000)
{
// map to store the numbers and their repetition
auto data = std::map<int, int>{};
// generate random numbers
for (auto n = 0; n < iterations; ++n)
++data[gen()];
// find the element with the most repetitions
auto max = std::max_element(
std::begin(data), std::end(data),
[](auto kvp1, auto kvp2) {
return kvp1.second < kvp2.second; });
// print the bars
for (auto i = max->second / 200; i > 0; --i)
{
for (auto kvp : data)
{
std::cout
<< std::fixed << std::setprecision(1) << std::setw(3)
<< (kvp.second / 200 > i ? (char)219 : ' ');
}
std::cout << '\n';
}
// print the numbers
for (auto kvp : data)
{
std::cout
<< std::fixed << std::setprecision(1) << std::setw(3)
<< kvp.first;
}
std::cout << '\n';
}
以下代码使用 std::mt19937 引擎生成随机数,这些随机数在 [1,6] 内均匀分布,这基本上是通过掷骰子能够得到的结果:
std::random_device rd{};
auto mtgen = std::mt19937{ rd() };
auto ud = std::uniform_int_distribution<>{ 1, 6 };
generate_and_print([&mtgen, &ud]() { return ud(mtgen); });
程序的输出如下图所示:
图 2 [1, 6] 内的均匀分布
在本节的最后一个示例中,我们将分布改为均值为 5、标准差为 2 的正态分布。这种分布生成实数,因此为了使用前面的 generate_and_print() 函数,数字必须四舍五入为整数:
std::random_device rd{};
auto mtgen = std::mt19937{ rd() };
auto nd = std::normal_distribution<>{ 5, 2 };
generate_and_print(
[&mtgen, &nd]() {
return static_cast<int>(std::round(nd(mtgen))); });
上述代码的输出结果如下图所示:
图 3 均值为5、标准差为2的正态分布
如图 3 所示,分布已经从均匀分布变为正态分布(均值为 5)。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: