C++双指针算法详解(附带实例)
双指针算法是一种针对数组进行操作的优化算法,它通过利用数据的单调性来降低时间复杂度,通常可以将一些原本时间复杂度为 O(n^2) 的问题降低为 O(n),效果非常显著。
使用双指针方法时,通常要求数组具备某种单调性质,例如数组是升序排列的,或者“区间内元素递增,所维护的值具有单调性”等。
以一个具体的问题为例,假设我们需要找到一个数组(数组最大长度和元素的最大值均为 10^5)中最长的连续不重复子序列的长度。即,我们需要寻找一个区间,其中没有重复元素,并且寻求这样的区间的最大长度。
考虑暴力解法,使用两个指针 i 和 j 来枚举数组中的所有区间,然后检查每个区间是否包含重复元素。可以想到一种小优化:在枚举过程中,动态地维护一个桶(由于本例中的数据范围较小,因此可以使用桶;如果数据范围较大,可以考虑使用 map 或 set 来检测重复元素),这样可以快速判断是否存在重复元素,但时间复杂度仍为 O(n^2)。
暴力代码如下:
那么问题来了,每次 r 都要从 l 重新开始遍历,真的有这个必要吗?
对于左端点为 l 的最大合法区间为 [l,r],当 l 移动到 l+1 时,对于所有 l+1≤k≤r:
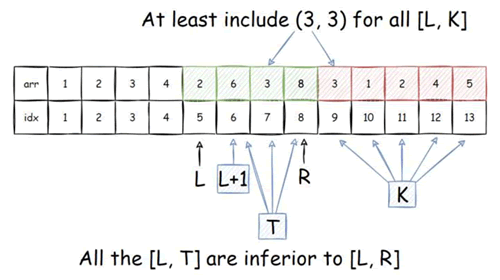
图 1 双指针单调性演示
如上图所示,所有 r 可以直接从上一轮结束的位置继续,即不需要移动 r,因此只需右移 l,r 两个指针,优化后的时间复杂度为 O(n)。
【实例】 最长连续不重复子序列。给定一个长度为 n(1≤n≤10^5)的数组 a(1≤ai≤10^5),求其中最长的连续不重复子序列的长度。
解题思路是,可以采用双指针的思想,l、r 指针只会向右移动,并用一个 bitset 记录元素是否出现过。
当区间 [l, r] 已经包含重复元素时,任何一个包含区间 [l, r] 的区间都必然会有重复元素,于是只要当 a[r + 1] 已经在区间 [l, r] 中出现过,右端点就没有必要再右移了,此时的最大合法区间为 [l, r]。
而当左端点右移一步后,因为此时的区间一定比最大合法区间更小,于是也没有必要让 r 回来重新跑一遍了。
实例代码如下:
使用双指针方法时,通常要求数组具备某种单调性质,例如数组是升序排列的,或者“区间内元素递增,所维护的值具有单调性”等。
以一个具体的问题为例,假设我们需要找到一个数组(数组最大长度和元素的最大值均为 10^5)中最长的连续不重复子序列的长度。即,我们需要寻找一个区间,其中没有重复元素,并且寻求这样的区间的最大长度。
考虑暴力解法,使用两个指针 i 和 j 来枚举数组中的所有区间,然后检查每个区间是否包含重复元素。可以想到一种小优化:在枚举过程中,动态地维护一个桶(由于本例中的数据范围较小,因此可以使用桶;如果数据范围较大,可以考虑使用 map 或 set 来检测重复元素),这样可以快速判断是否存在重复元素,但时间复杂度仍为 O(n^2)。
暴力代码如下:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
ll a[N];
void solve() {
int n; cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
int ans = 0;
for (int i = 1; i <= n; ++i) {
bitset<N> vis;
for (int j = i; j <= n; ++j) {
// 枚举到区间 [i, j]
// 判断是否已经存在 a[j],若存在则可以直接 break
if (vis[a[j]]) break;
vis[a[j]] = true;
// 如果没有 break,则说明区间 [i, j] 不存在重复元素
ans = max(ans, j - i + 1);
}
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t; cin >> t;
while (t--) solve();
return 0;
}
接下来考虑如何优化这个问题。假设当前区间为 [l,r],且 [l,r+1] 已经出现了重复元素,即 [l,r] 为左端点为 l 时的最大合法区间。对于所有 k>r 的区间,[l,k] 必然存在重复元素,因此可以直接 break,这在暴力代码中已经有所体现。那么问题来了,每次 r 都要从 l 重新开始遍历,真的有这个必要吗?
对于左端点为 l 的最大合法区间为 [l,r],当 l 移动到 l+1 时,对于所有 l+1≤k≤r:
- 若 [l,k] 合法,则长度必然小于 r−l+1,且都不如 [l,r] 优秀,因此无须再遍历,可以让 r 延续上一轮的位臵。
- 若 [l,k] 不合法,则需要右移 l,r 无须改变。

图 1 双指针单调性演示
如上图所示,所有 r 可以直接从上一轮结束的位置继续,即不需要移动 r,因此只需右移 l,r 两个指针,优化后的时间复杂度为 O(n)。
具体的实现代码请见本节例题。
双指针的类型
常见的双指针类型有以下 4 种:- 快慢指针:一般用于解决链表中的循环检测问题,在算法竞赛中涉及较少,因此不再深入阐述;
- 左右指针:在有序数组中查找一对特定的数字,通常用于枚举二元组或区间;
- 对撞双指针:利用某些数学特性(单调性),初始区间为 [1,n],每次只移动一个指针,从而不断逼近最大值。典型题目有:盛最多水的容器;
- 滑动窗口:用于维护一段区间的各种统计信息,例如最值或元素的总和,常见于在单调队列中维护最值。
【实例】 最长连续不重复子序列。给定一个长度为 n(1≤n≤10^5)的数组 a(1≤ai≤10^5),求其中最长的连续不重复子序列的长度。
解题思路是,可以采用双指针的思想,l、r 指针只会向右移动,并用一个 bitset 记录元素是否出现过。
当区间 [l, r] 已经包含重复元素时,任何一个包含区间 [l, r] 的区间都必然会有重复元素,于是只要当 a[r + 1] 已经在区间 [l, r] 中出现过,右端点就没有必要再右移了,此时的最大合法区间为 [l, r]。
而当左端点右移一步后,因为此时的区间一定比最大合法区间更小,于是也没有必要让 r 回来重新跑一遍了。
实例代码如下:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
ll a[N];
void solve() {
int n; cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
int ans = 0;
bitset<N> vis;
for (int i = 1, j = 0; i <= n; ++i) {
while (j < n && !vis[a[j + 1]]) vis[a[++j]] = true;
// 此时的 [i, j] 是以 i 为左端点的最大合法区间
ans = max(ans, j - i + 1);
// 注意在 i 右移时,需要将 a[i] 移除
vis[a[i]] = false;
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t; cin >> t;
while (t--) solve();
return 0;
}
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: